Link Search Menu Expand Document

In the case of a $3\times 3$ matrix there are four classes of numerical ranges [1]:

  • Numerical range with zero line segments (ovular)
  • Numerical range with one line segment
  • Numerical range with two line segments
  • Numerical range with three line segments (triangular)

Example 1

  • The matrix $M=\begin{pmatrix}1&1&1\\0&\ee^{\frac{2\ii}{3}}&1\\0&0&\ee^{\frac{4\ii}{3}}\end{pmatrix}$ has an ovular numerical range
Example of a numerical range whose boundary includes zero line segments.
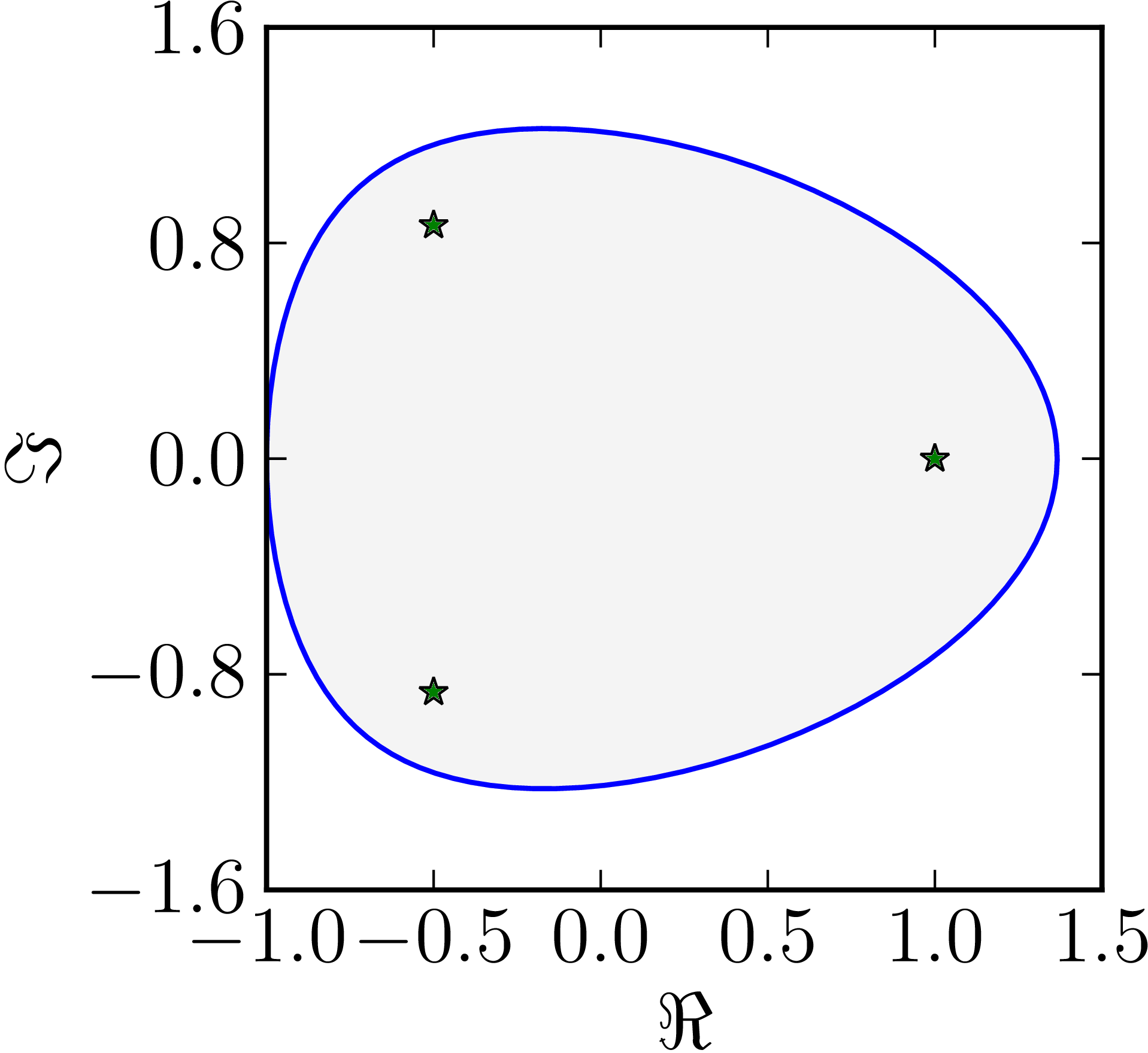Example of an ovular numerical range

Example 2

  • The matrix $M= $ has a numerical range whose boundary includes one line segment
Example of a numerical range whose boundary includes one line segment.
Example of a numerical range whose boundary includes one line segment

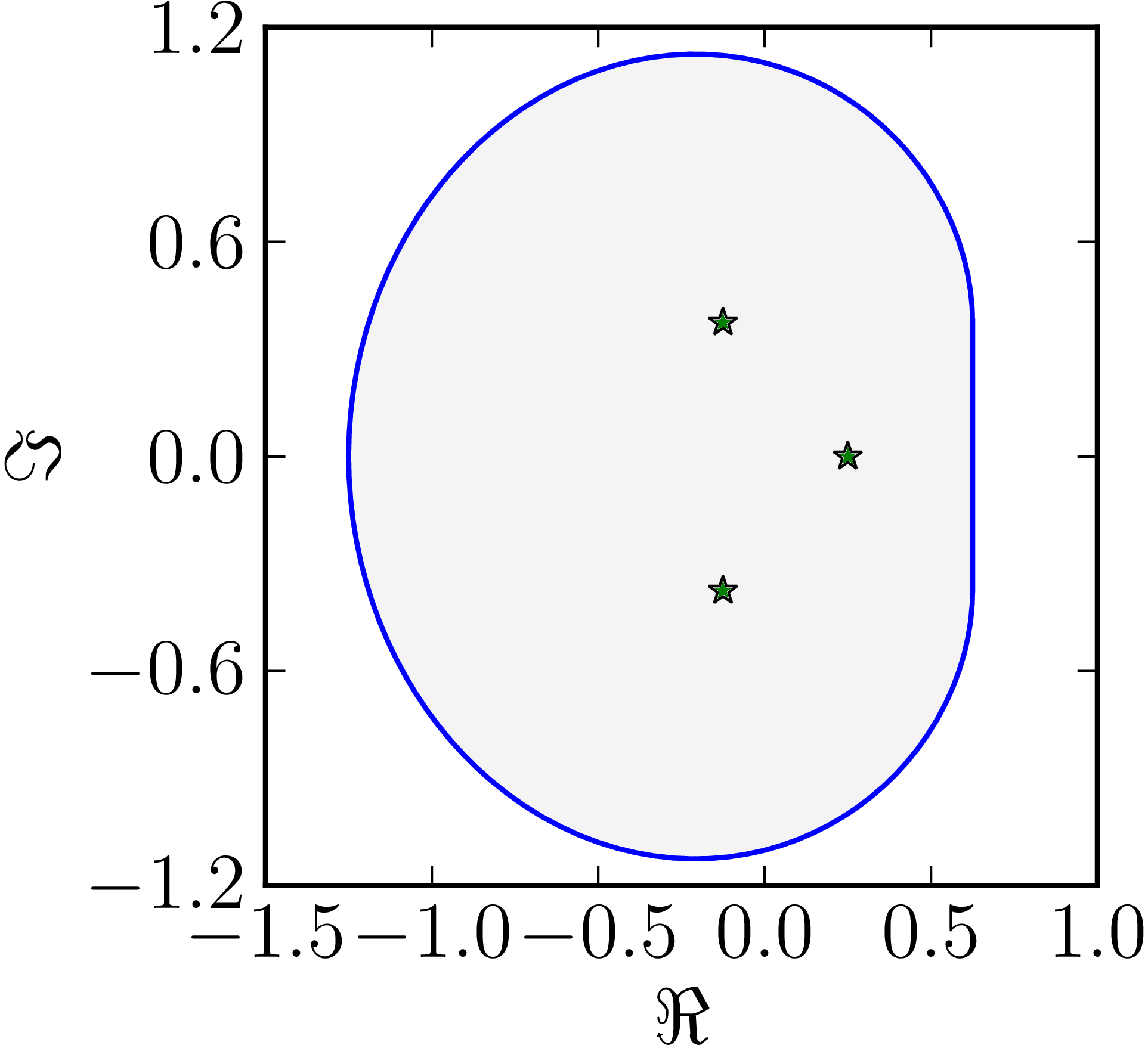Example 3

  • The matrix $M=\begin{pmatrix}1&1&0\\0&\ee^{\frac{2\ii}{3}}&0\\0&0&\ee^{\frac{4\ii}{3}}\end{pmatrix}$ has a numerical range whose boundary includes two line segments
Example of a numerical range whose boundary includes two line segments.
Example of a numerical range whose boundary includes two line segments

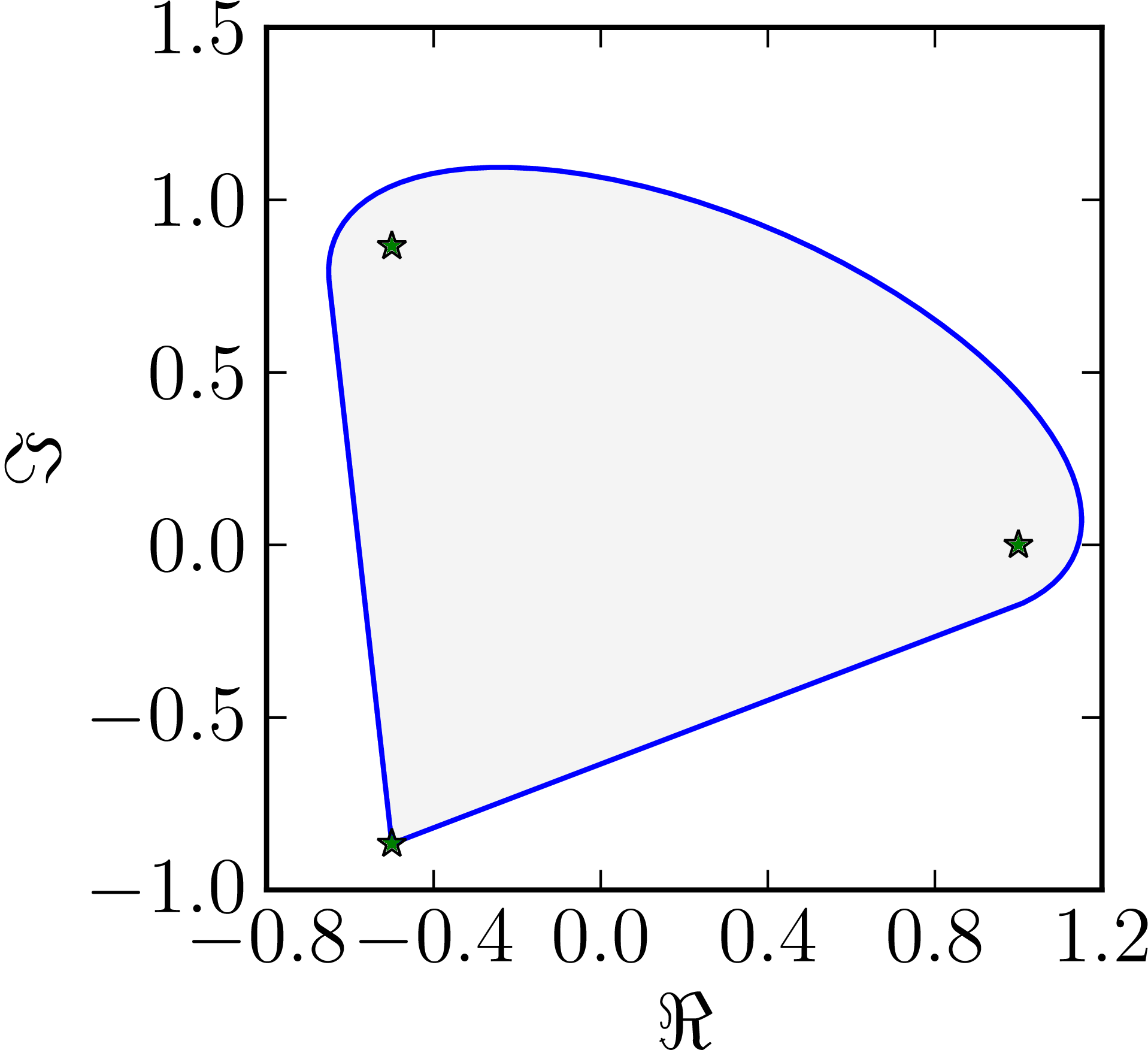Example 4

  • The matrix $M=\begin{pmatrix}1&0&0\\0&\ee^{\frac{2\ii}{3}}&0\\0&0&\ee^{\frac{4\ii}{3}}\end{pmatrix}$ has a triangular numerical range. Notice that the matrix is normal.
Example of a numerical range whose boundary includes three line segments.
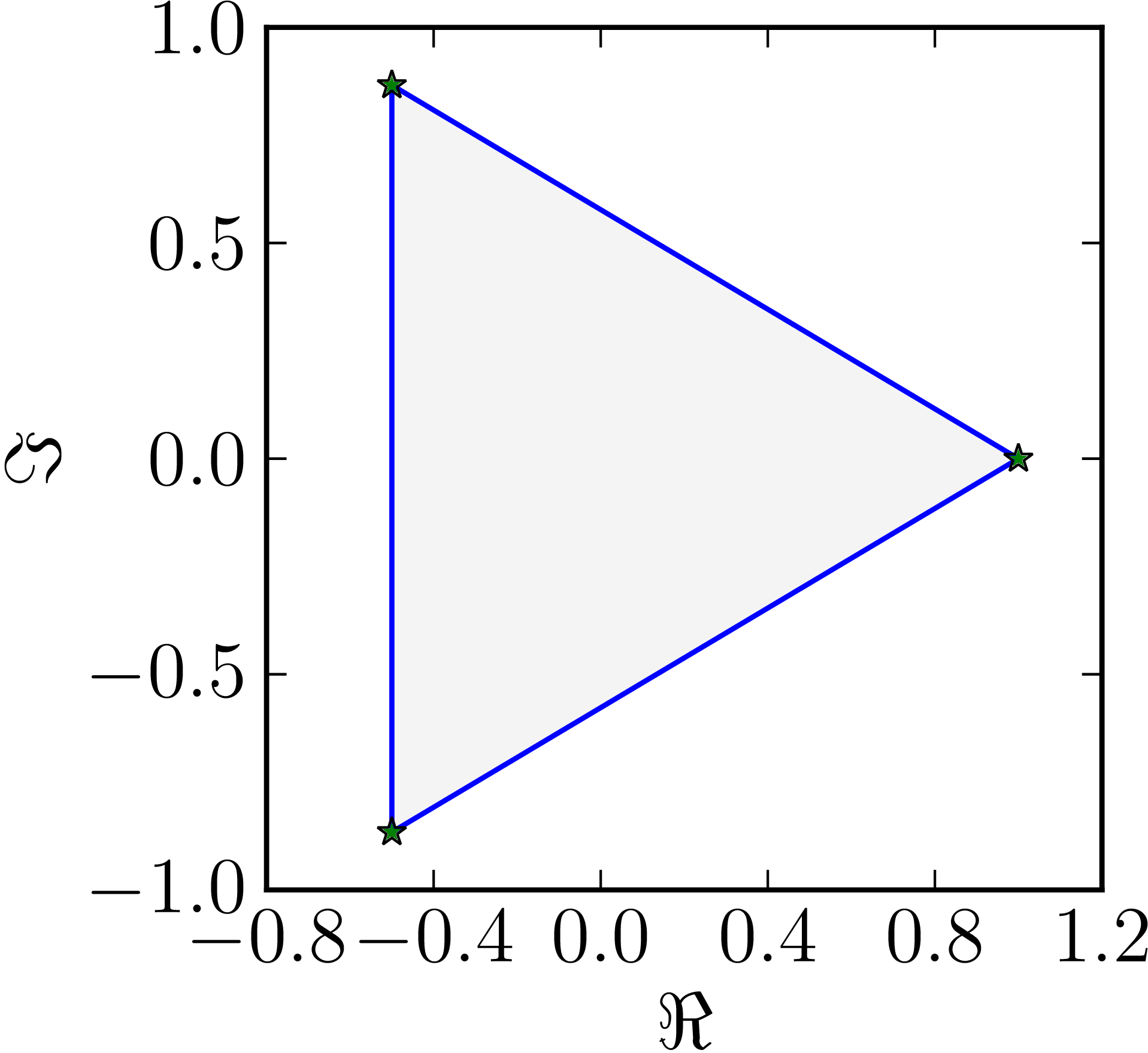Example of a triangular numerical range

References

  1. [1]D. S. Keeler, L. Rodman, and I. M. Spitkovsky, “The numerical range of 3x3 matrices,” Linear Algebra and its Applications, vol. 252, no. 1-3, pp. 115–139, 1997, [Online]. Available at: https://dx.doi.org/10.1016/0024-3795(95)00674-5.