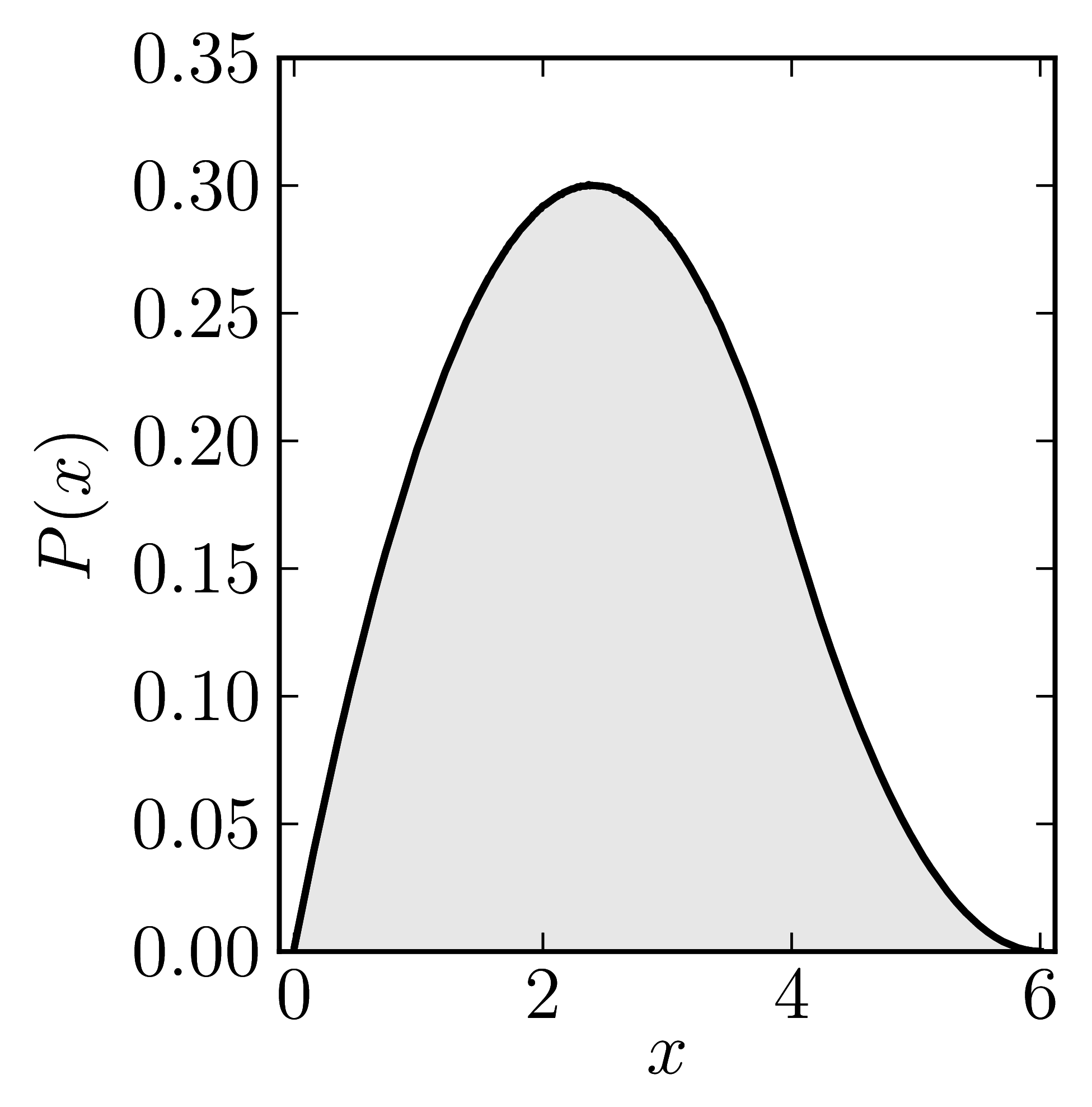
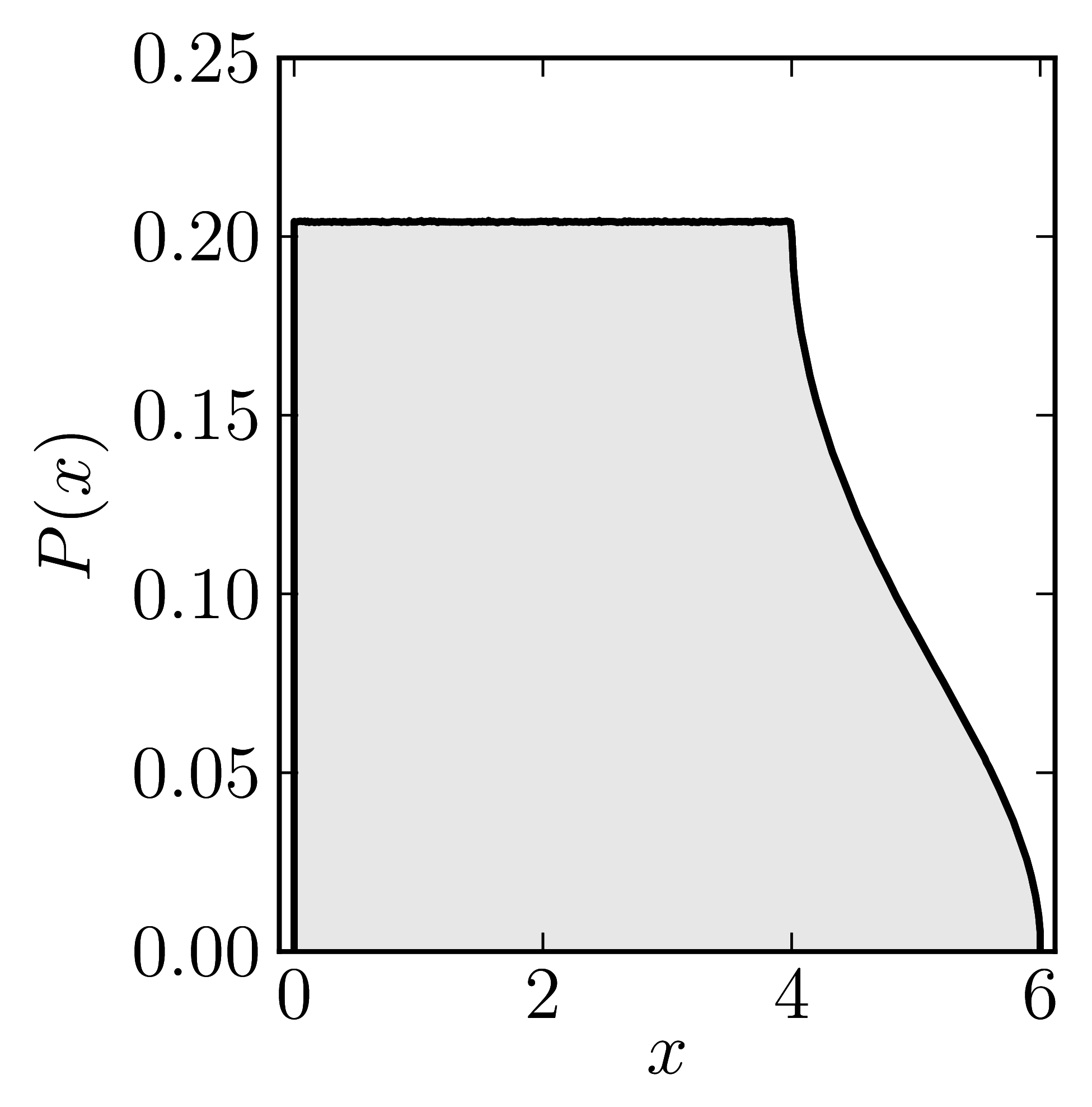
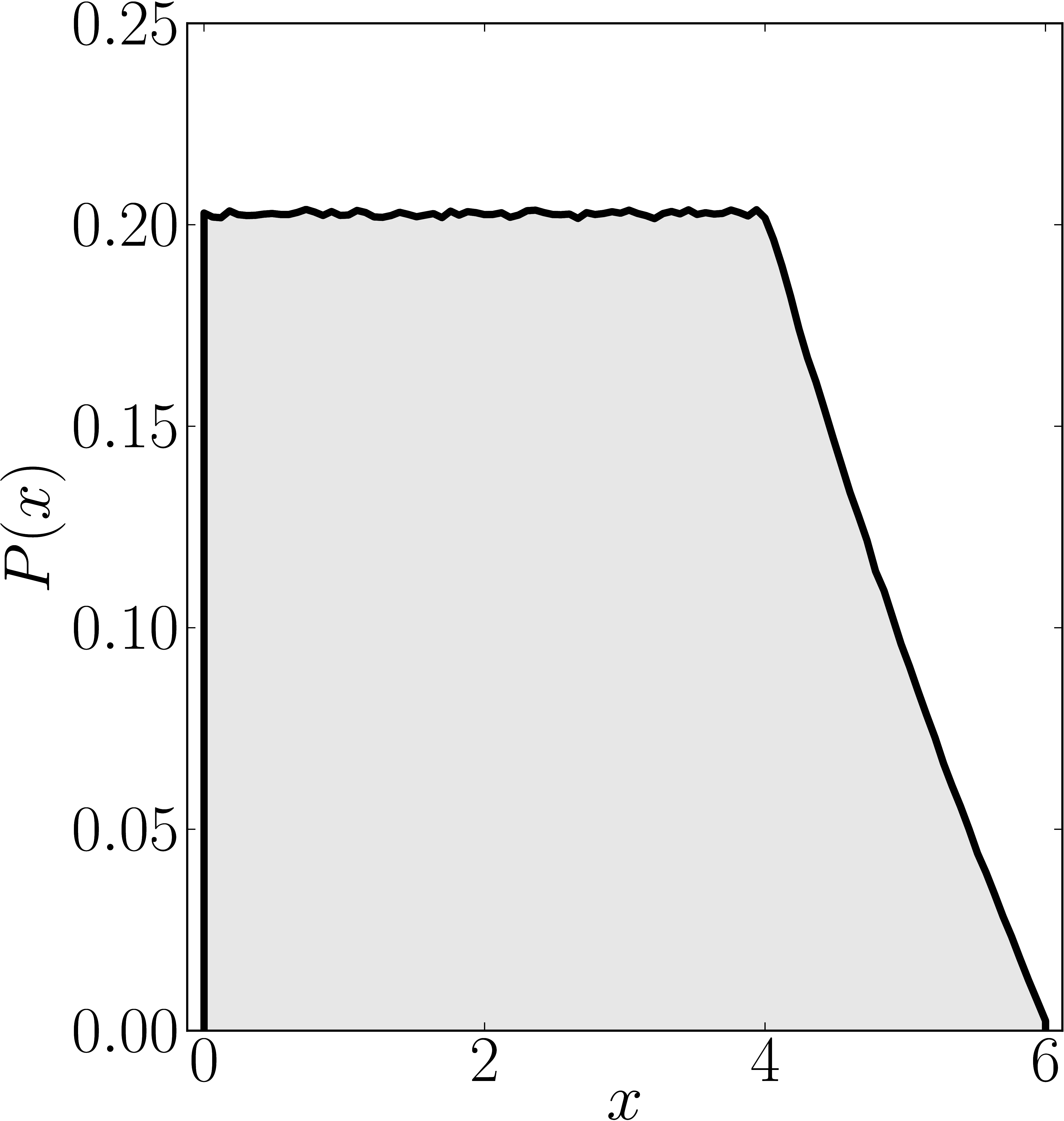
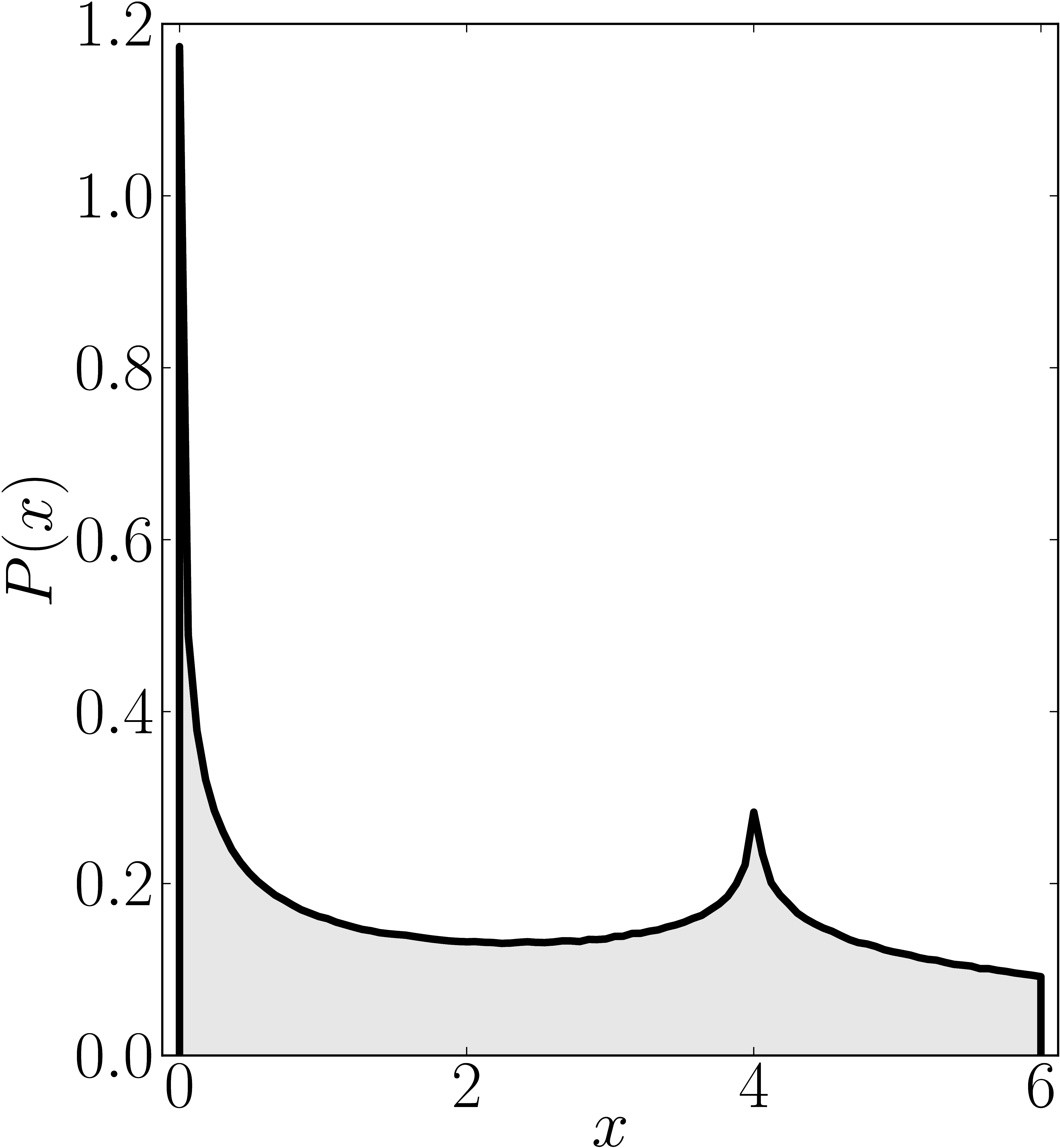
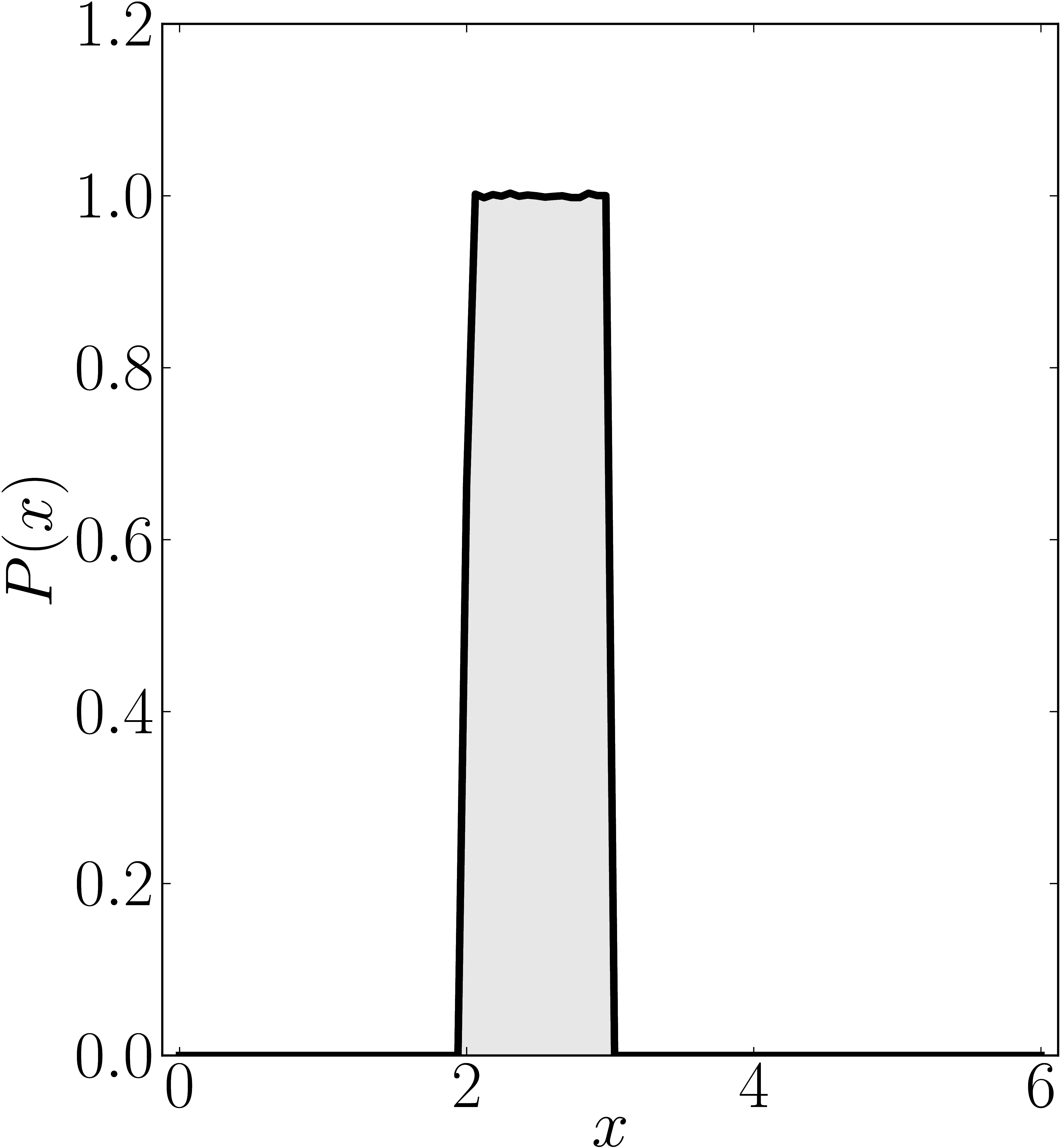
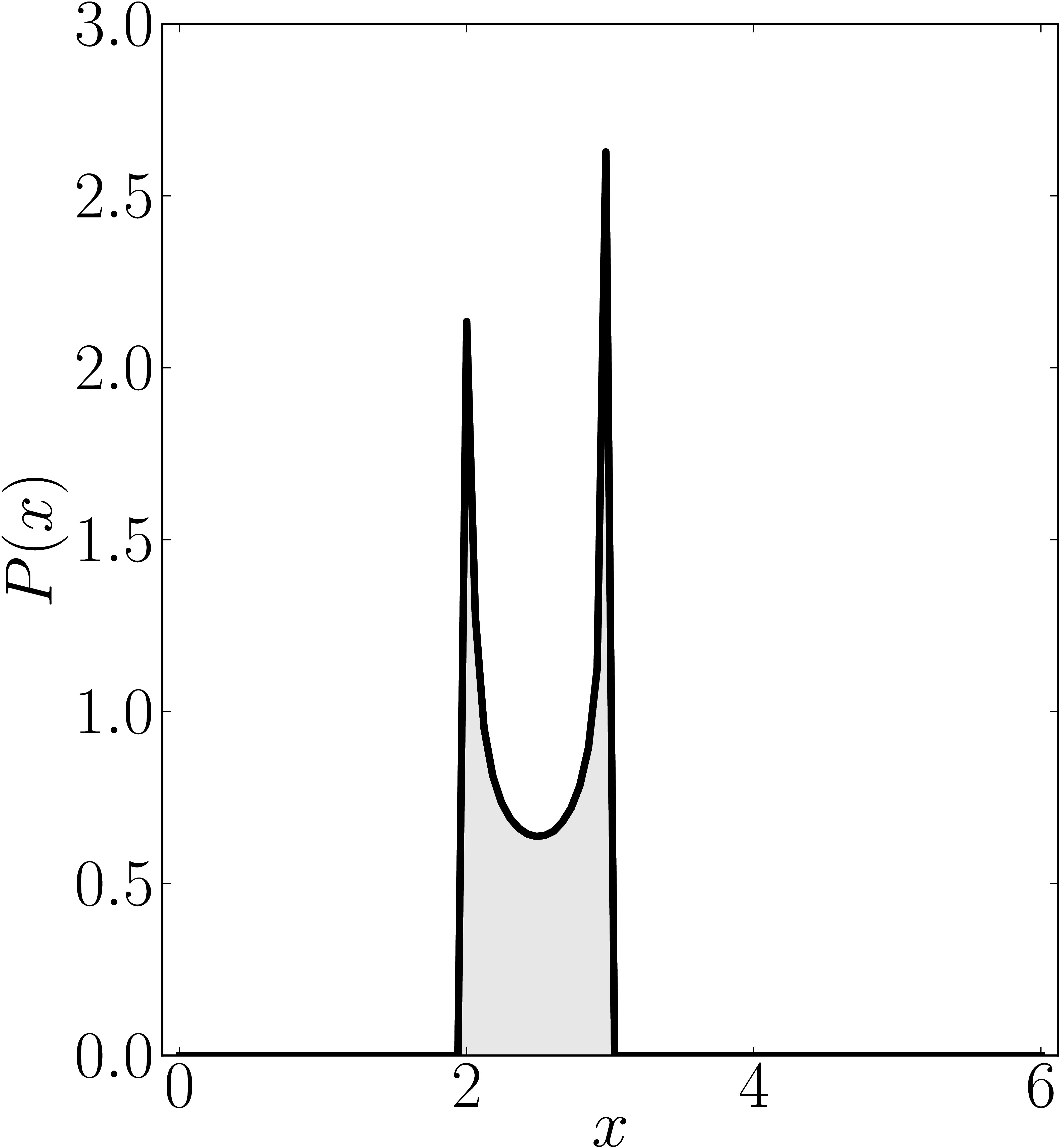
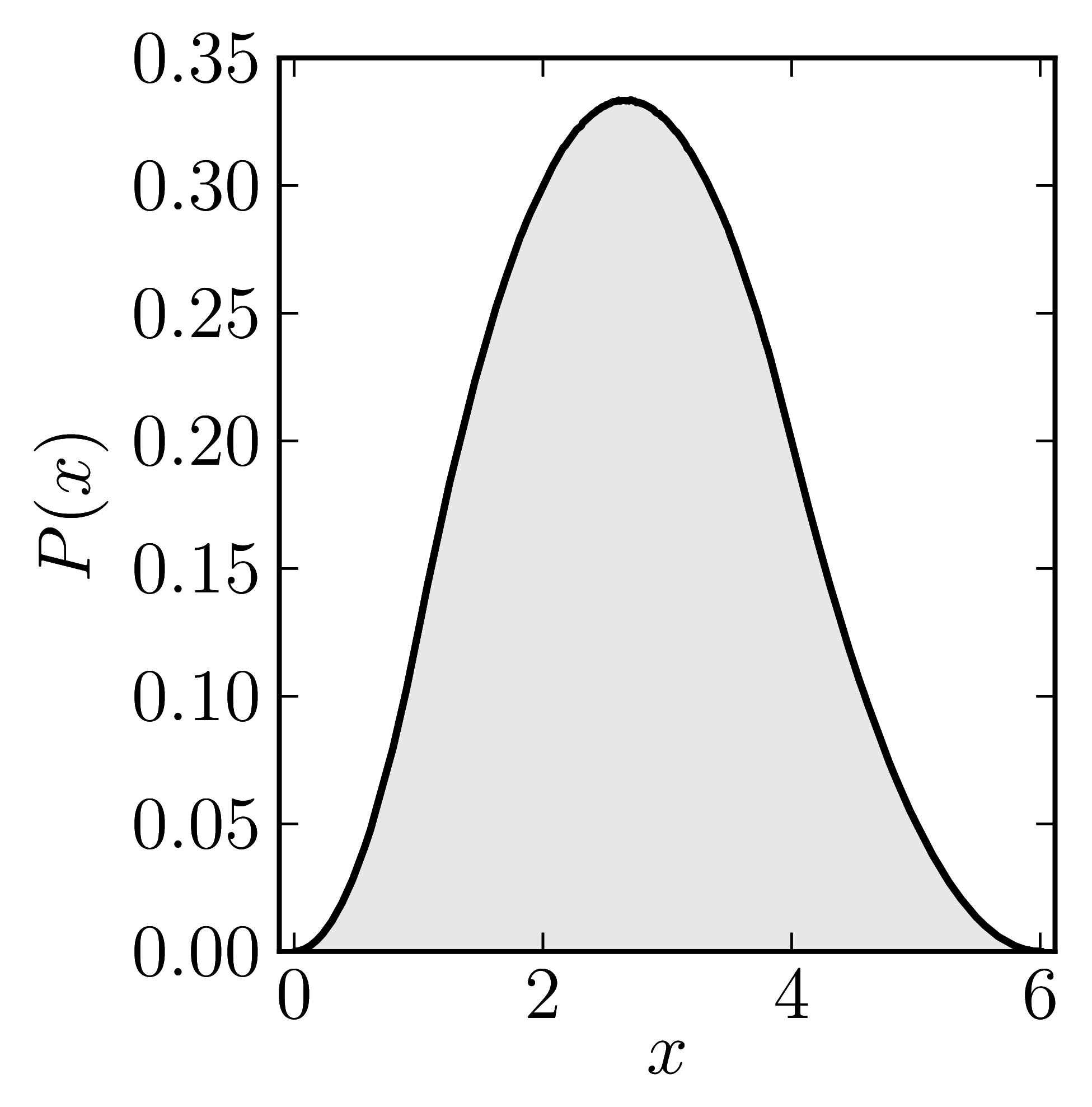
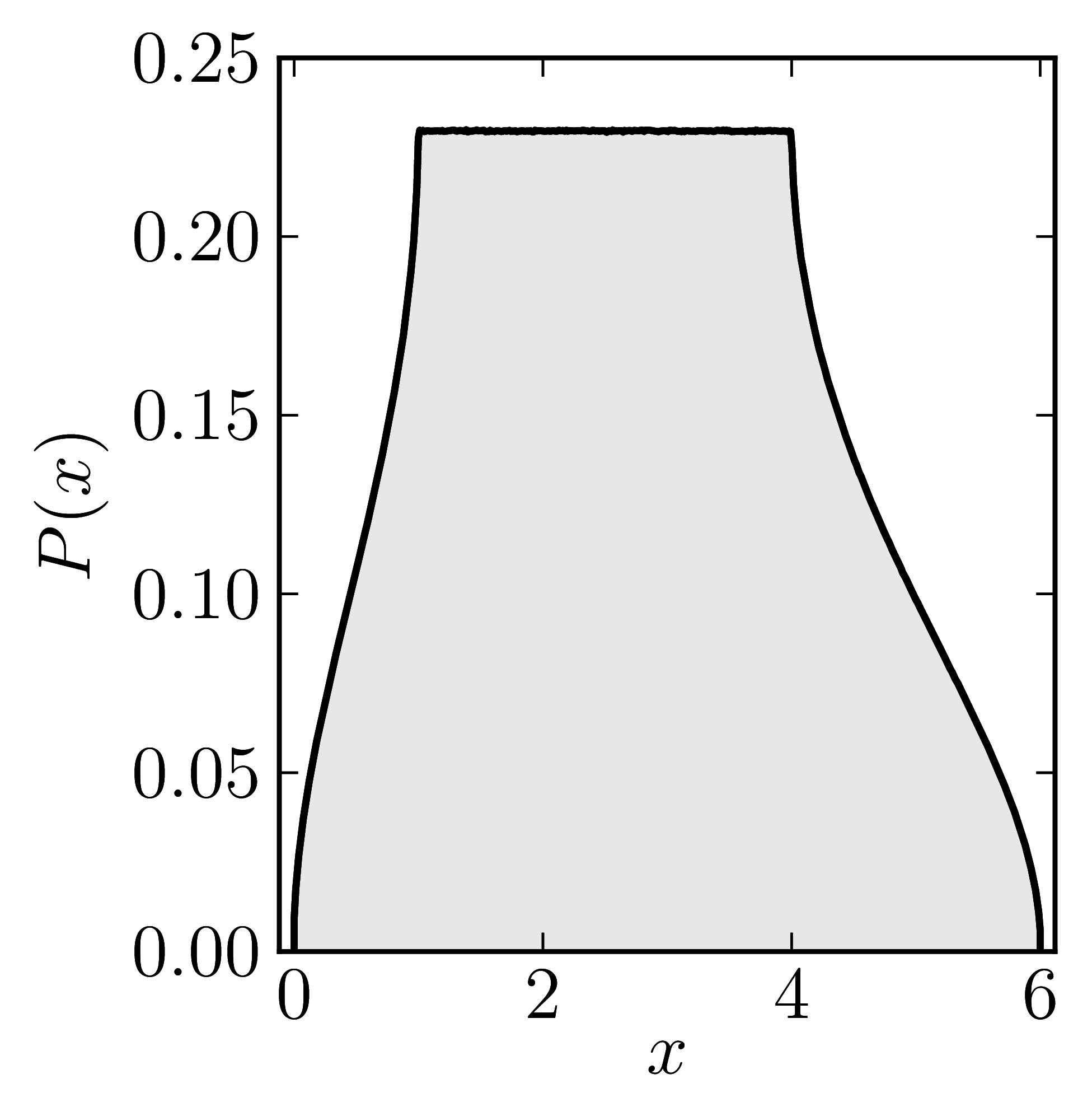
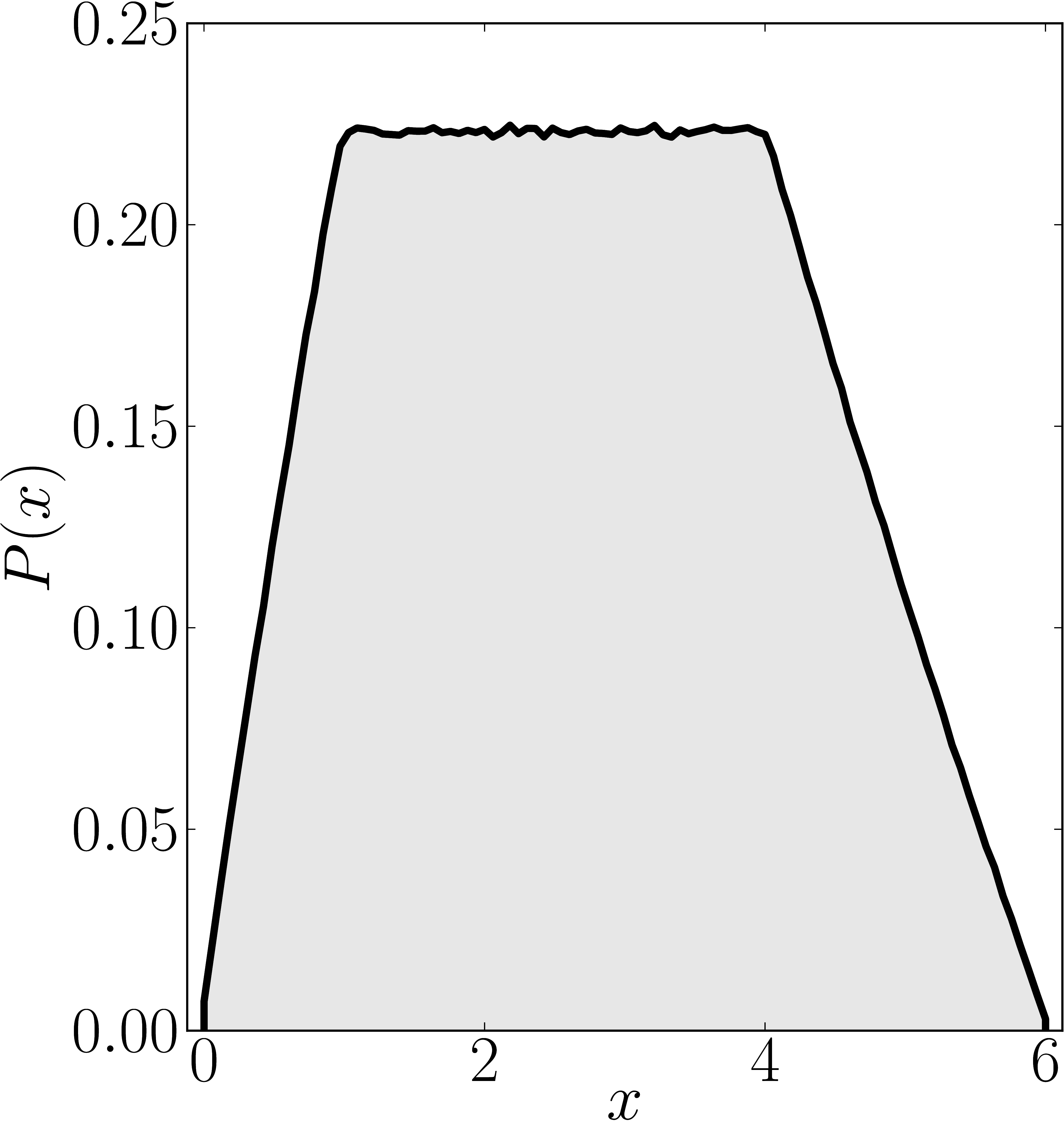
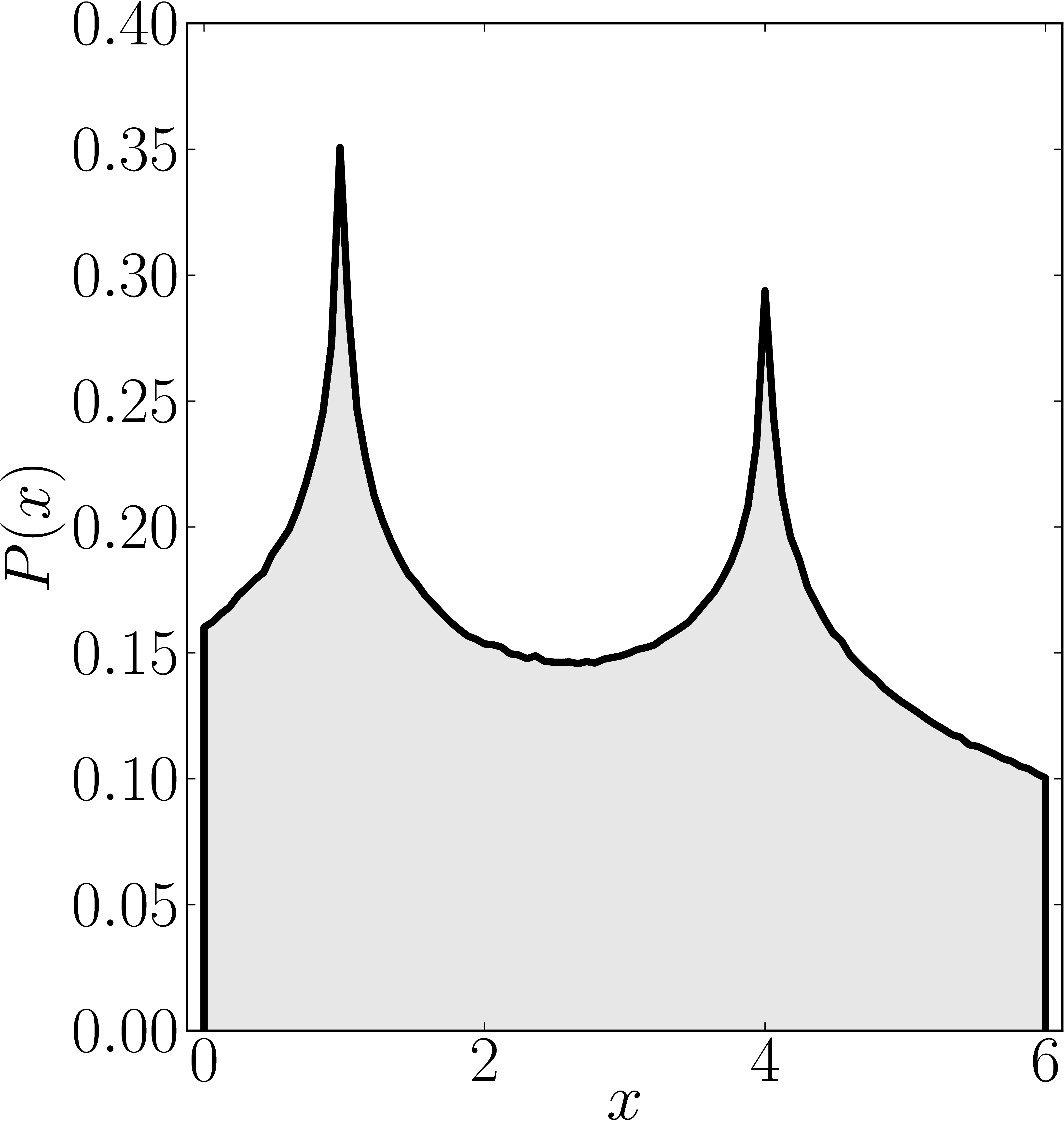
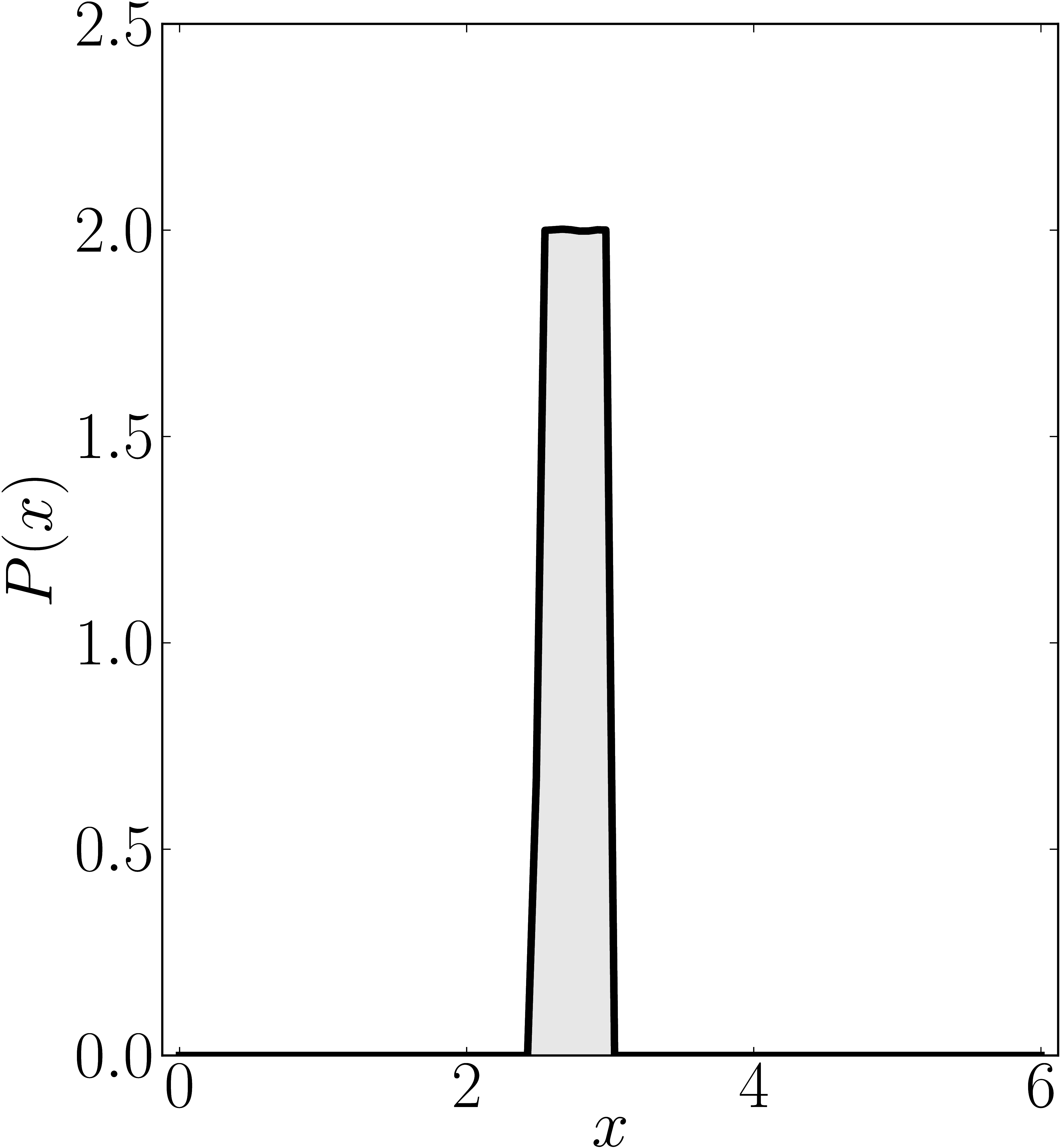
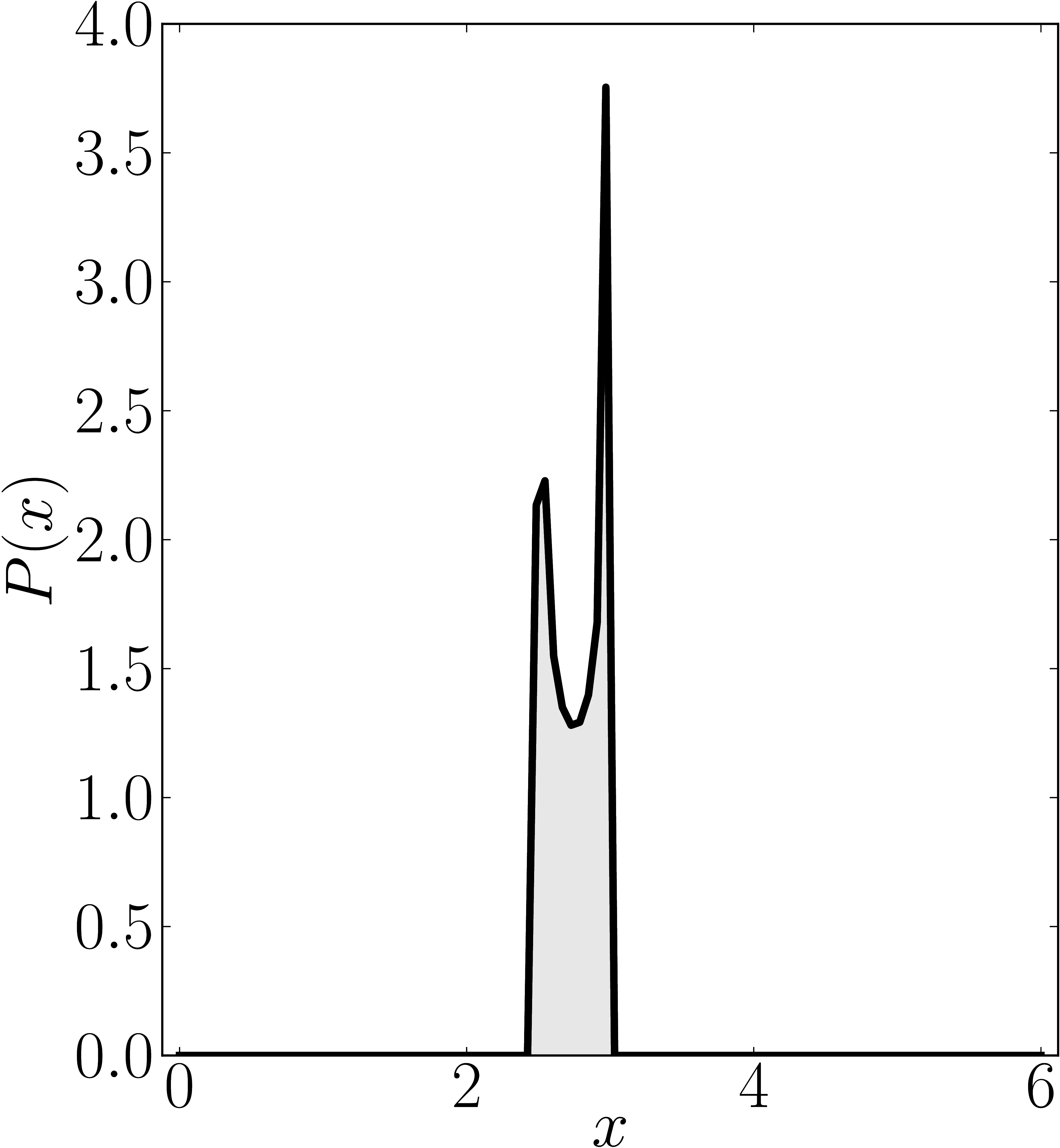
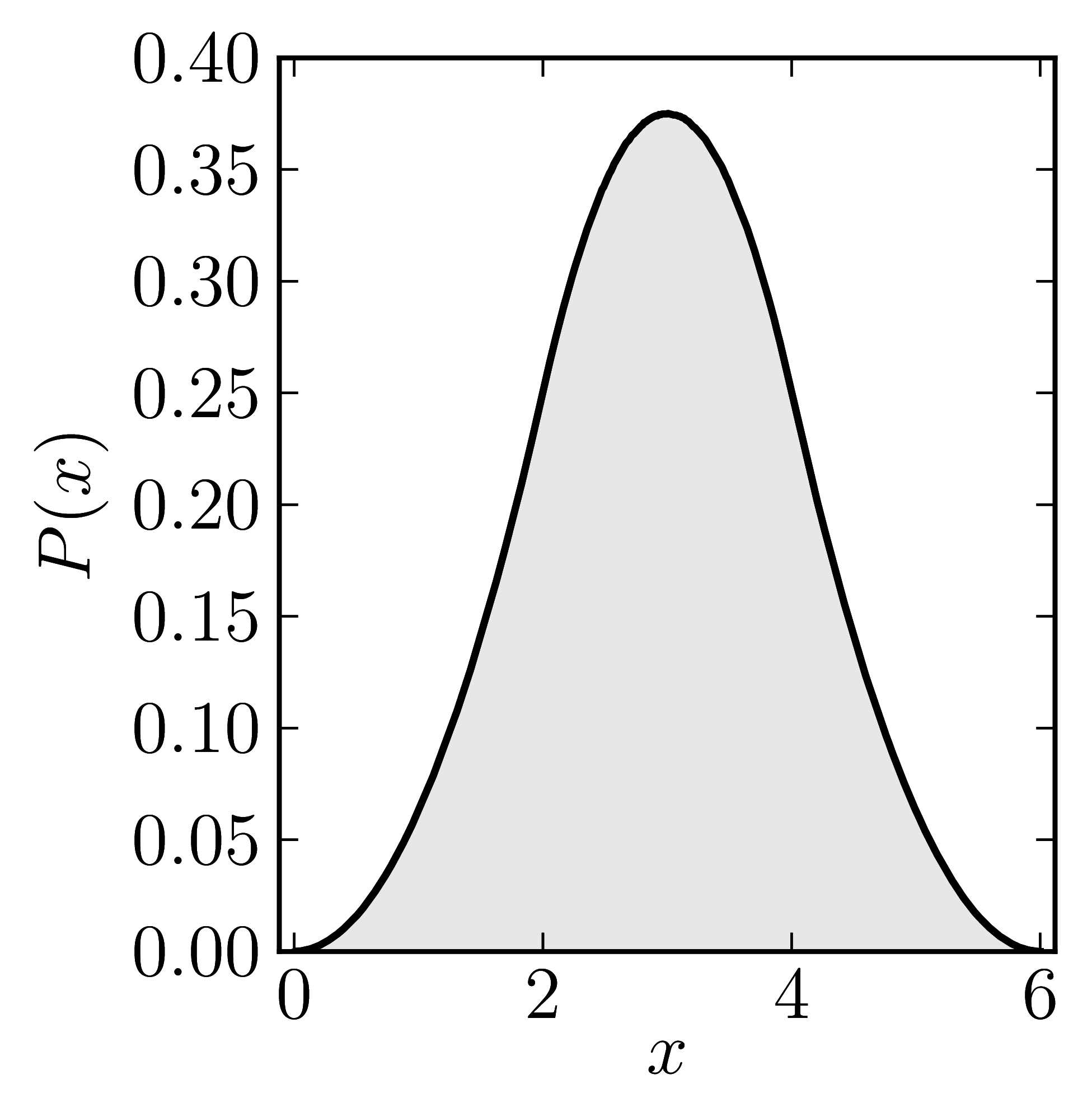
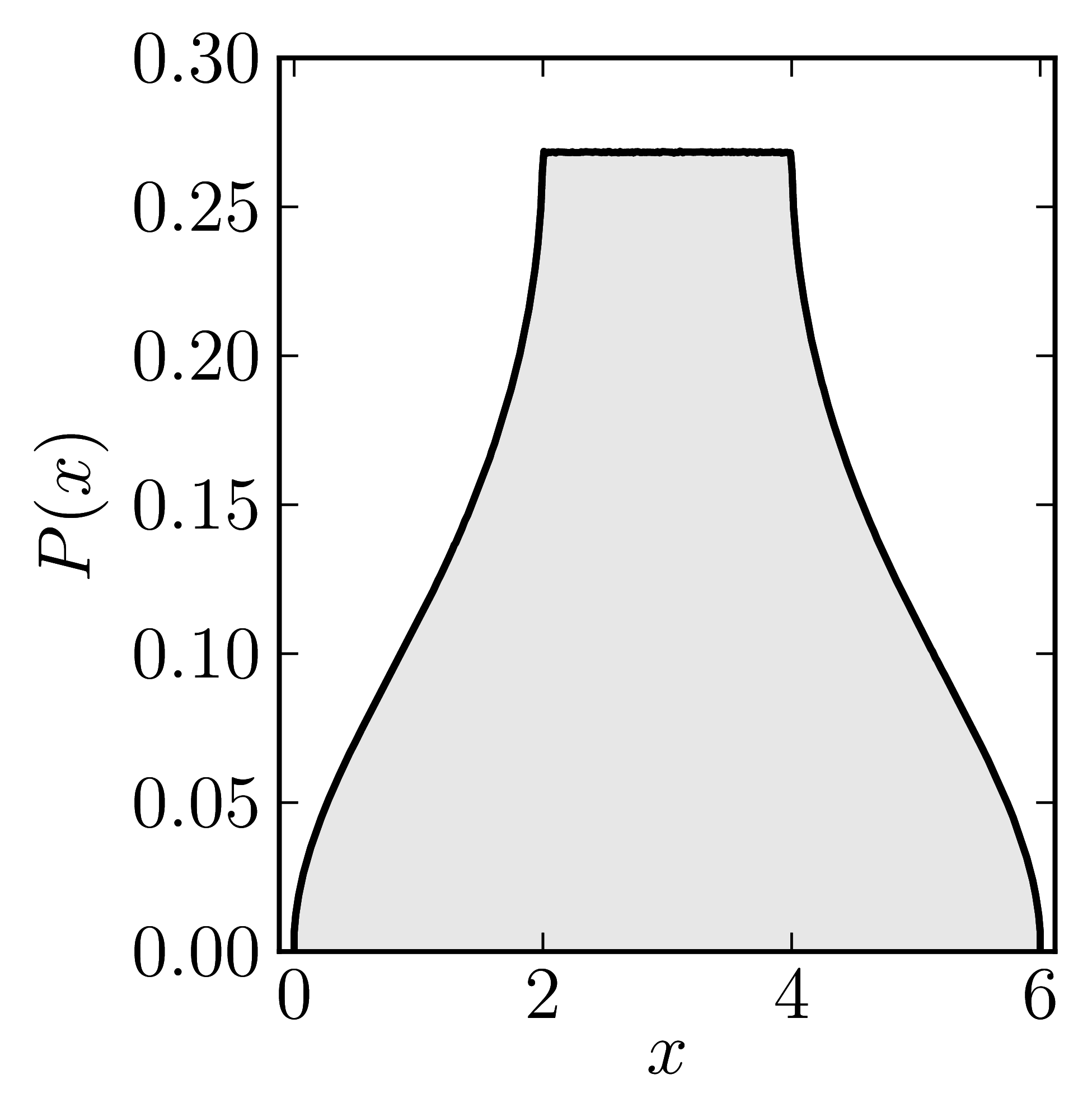
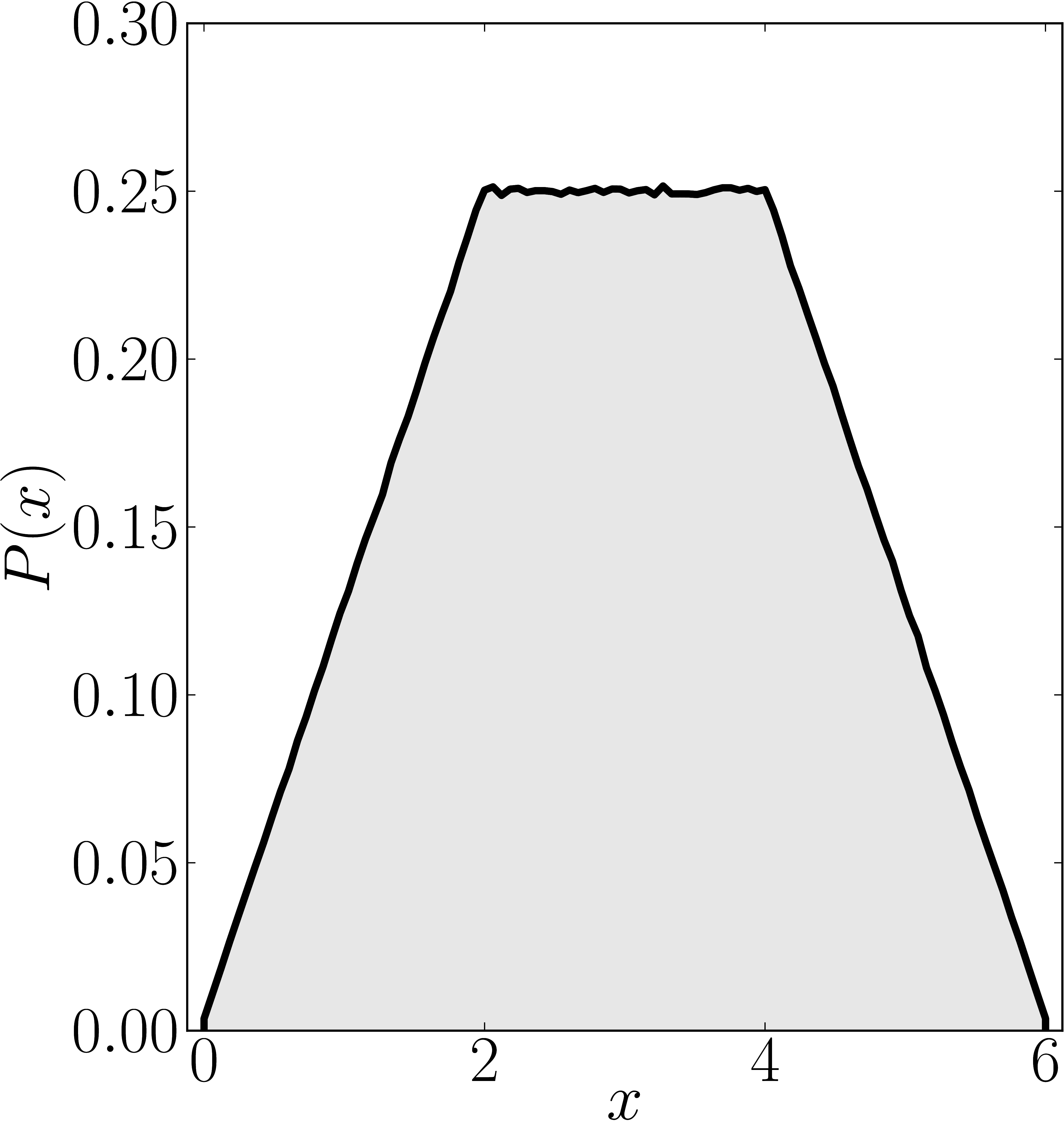
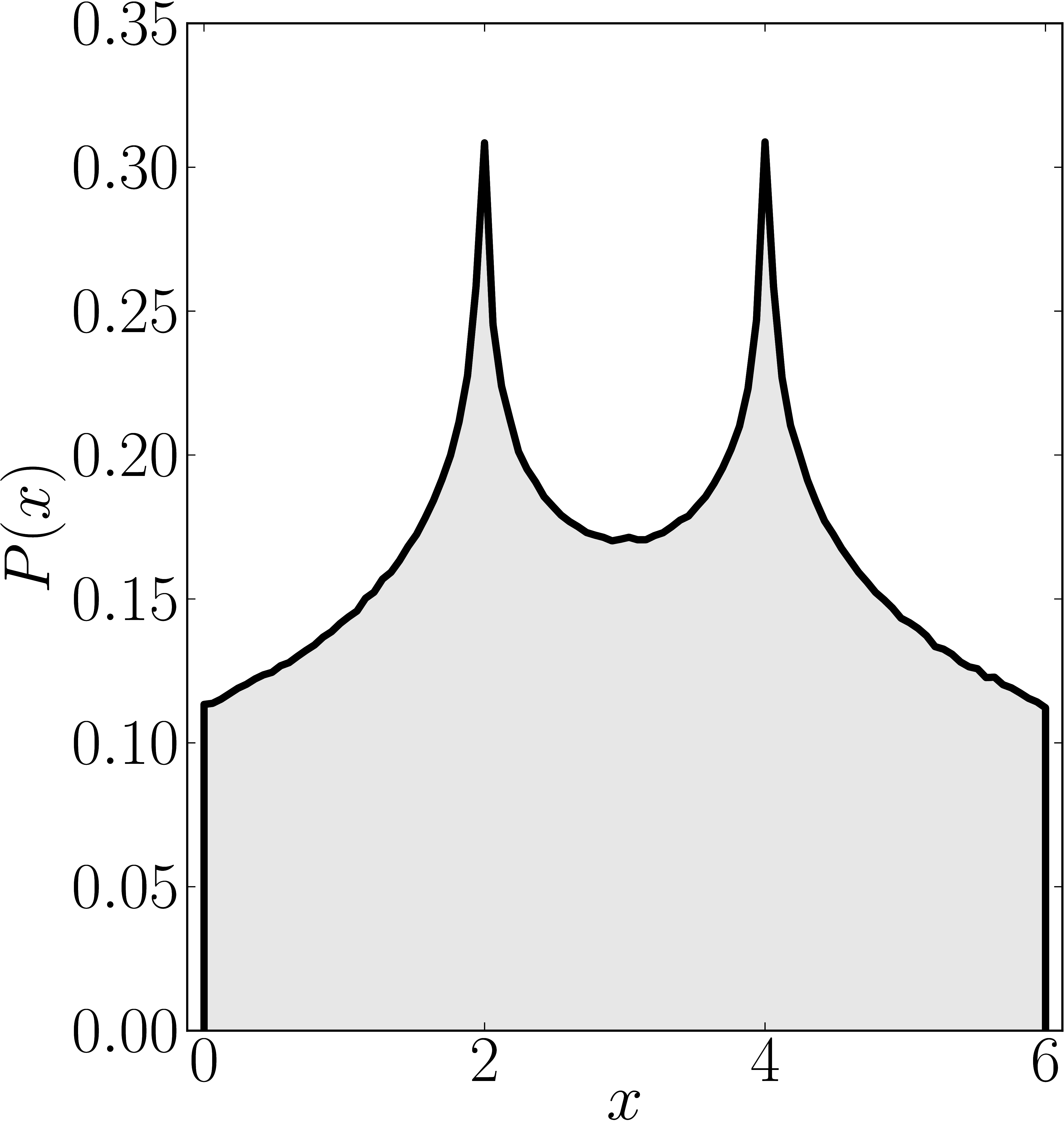
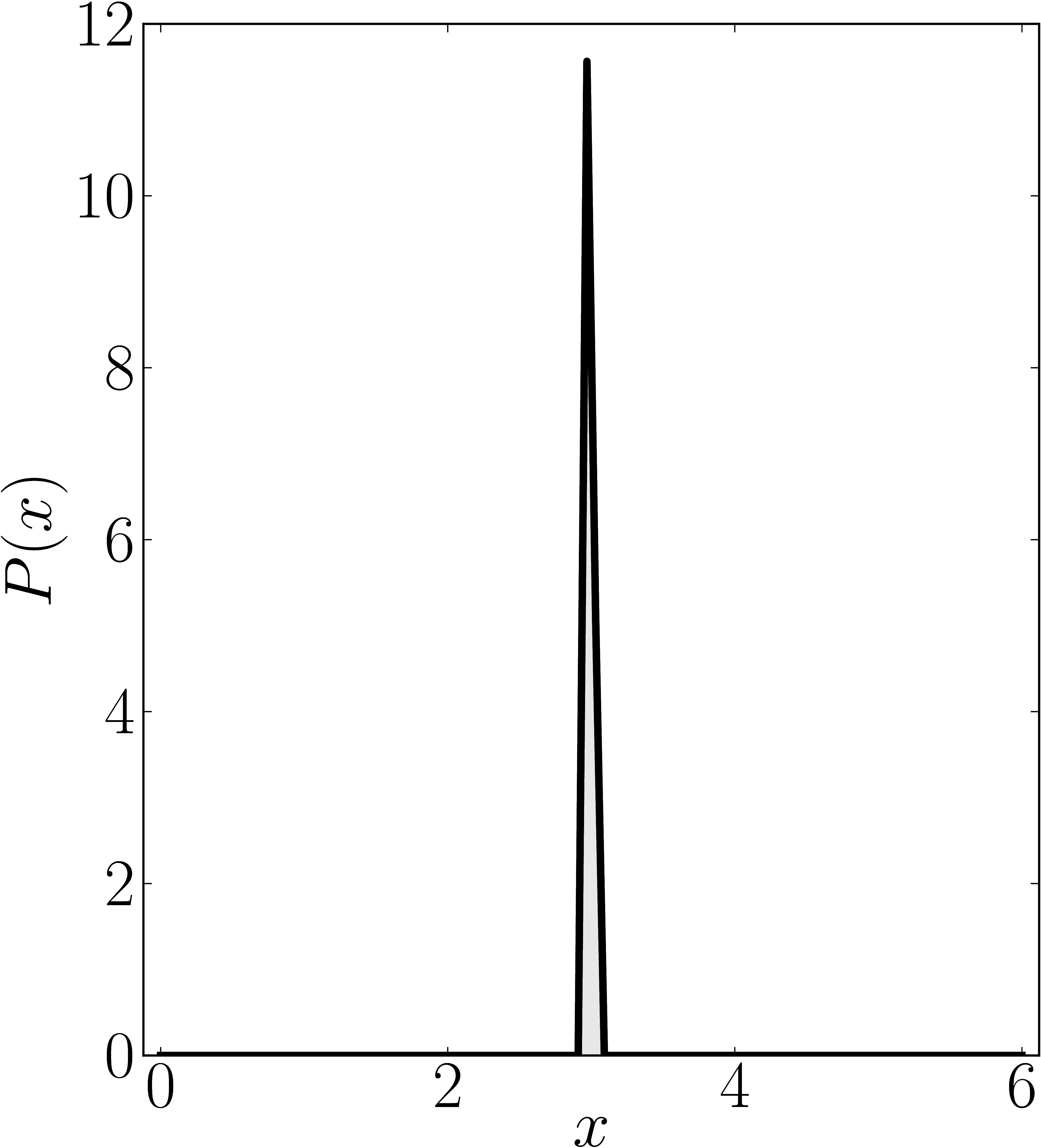
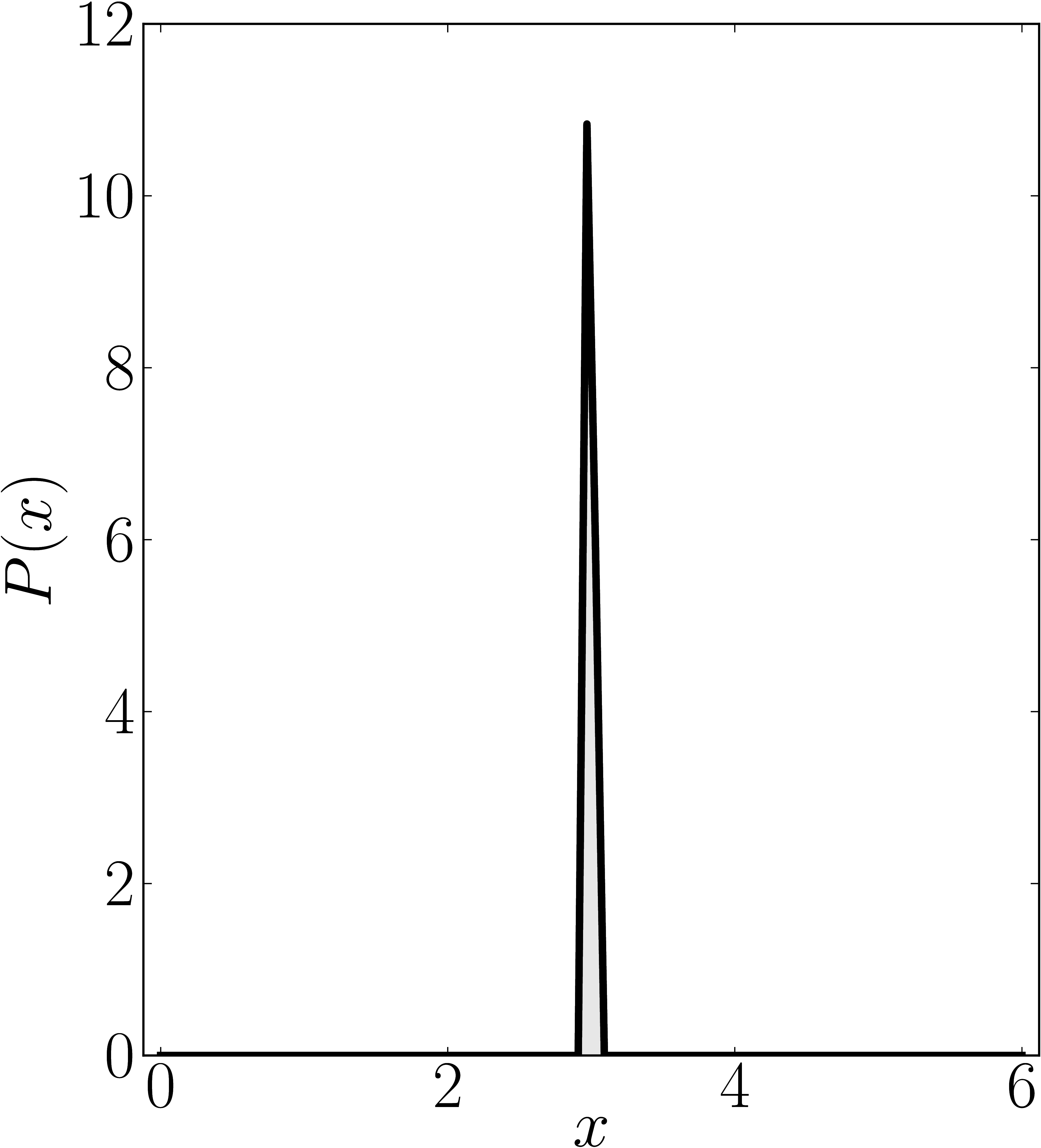
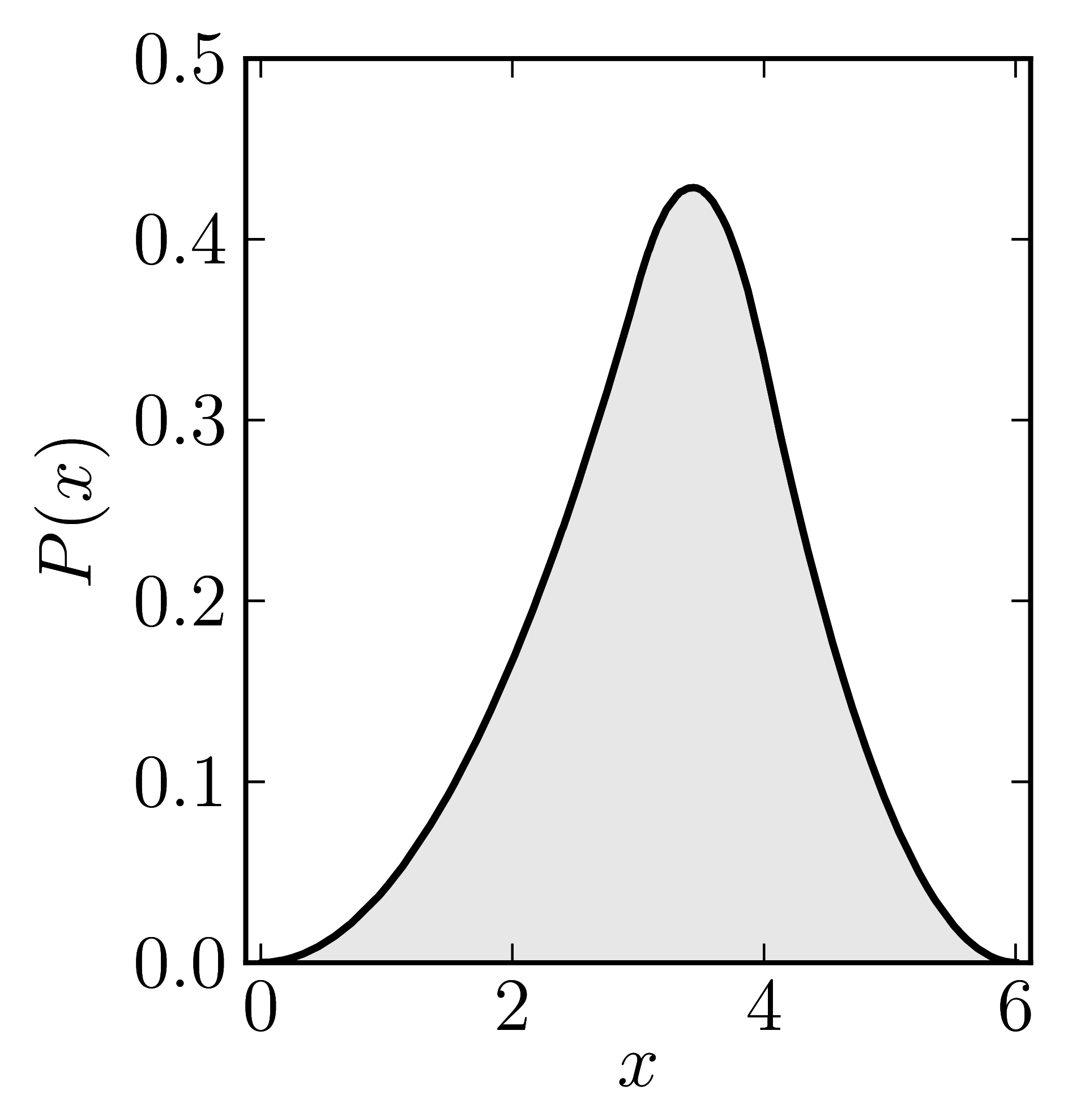
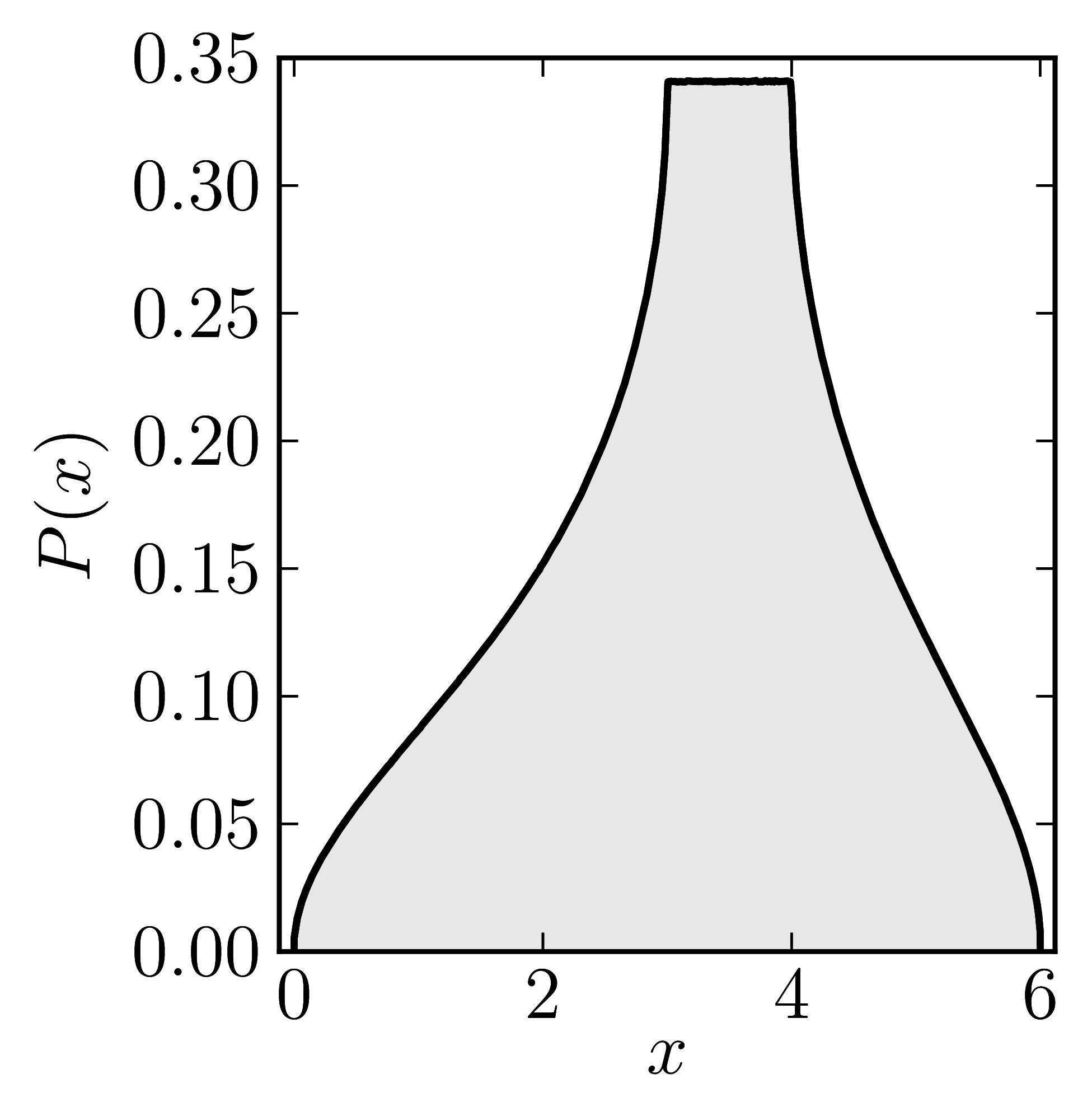
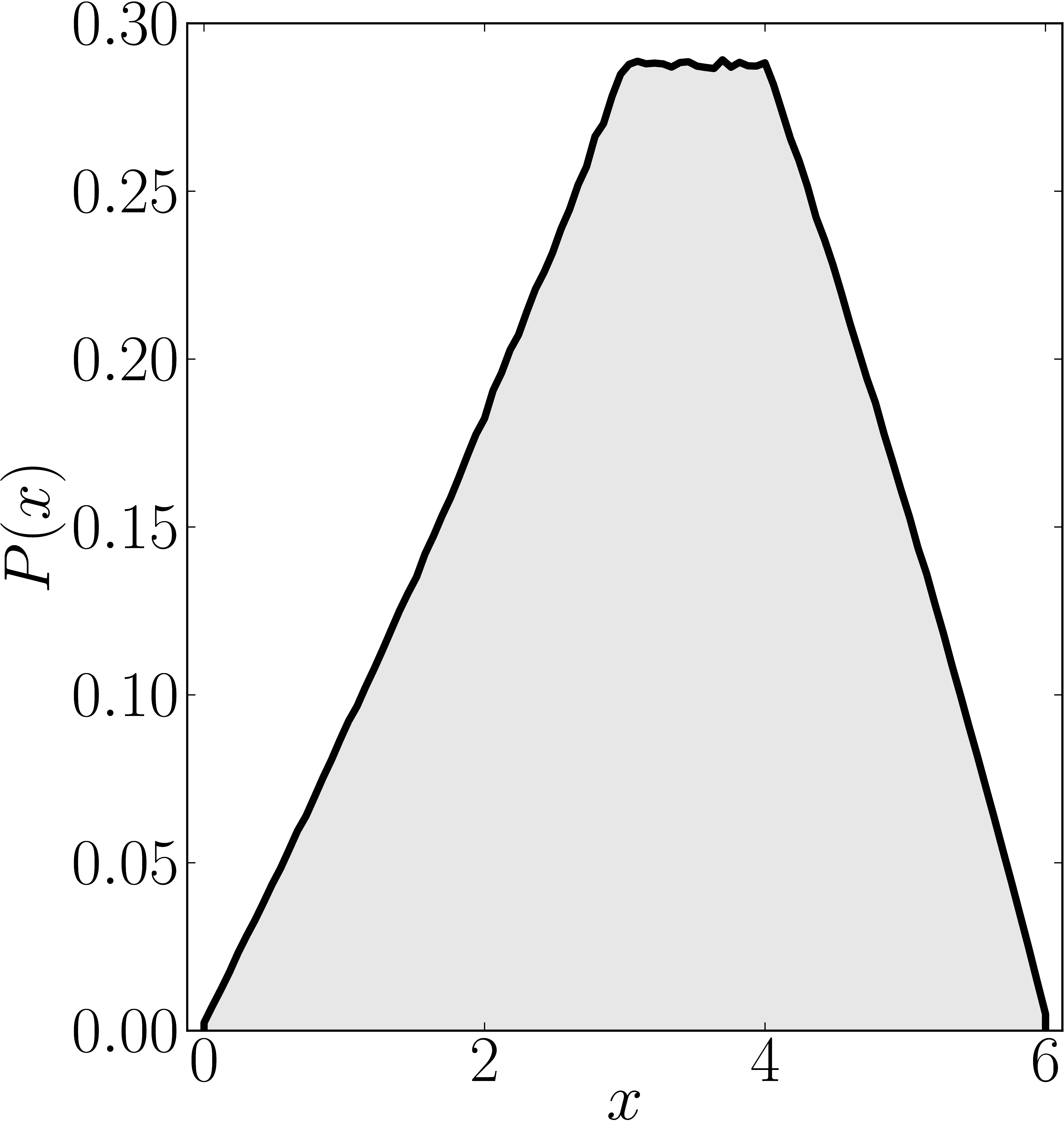
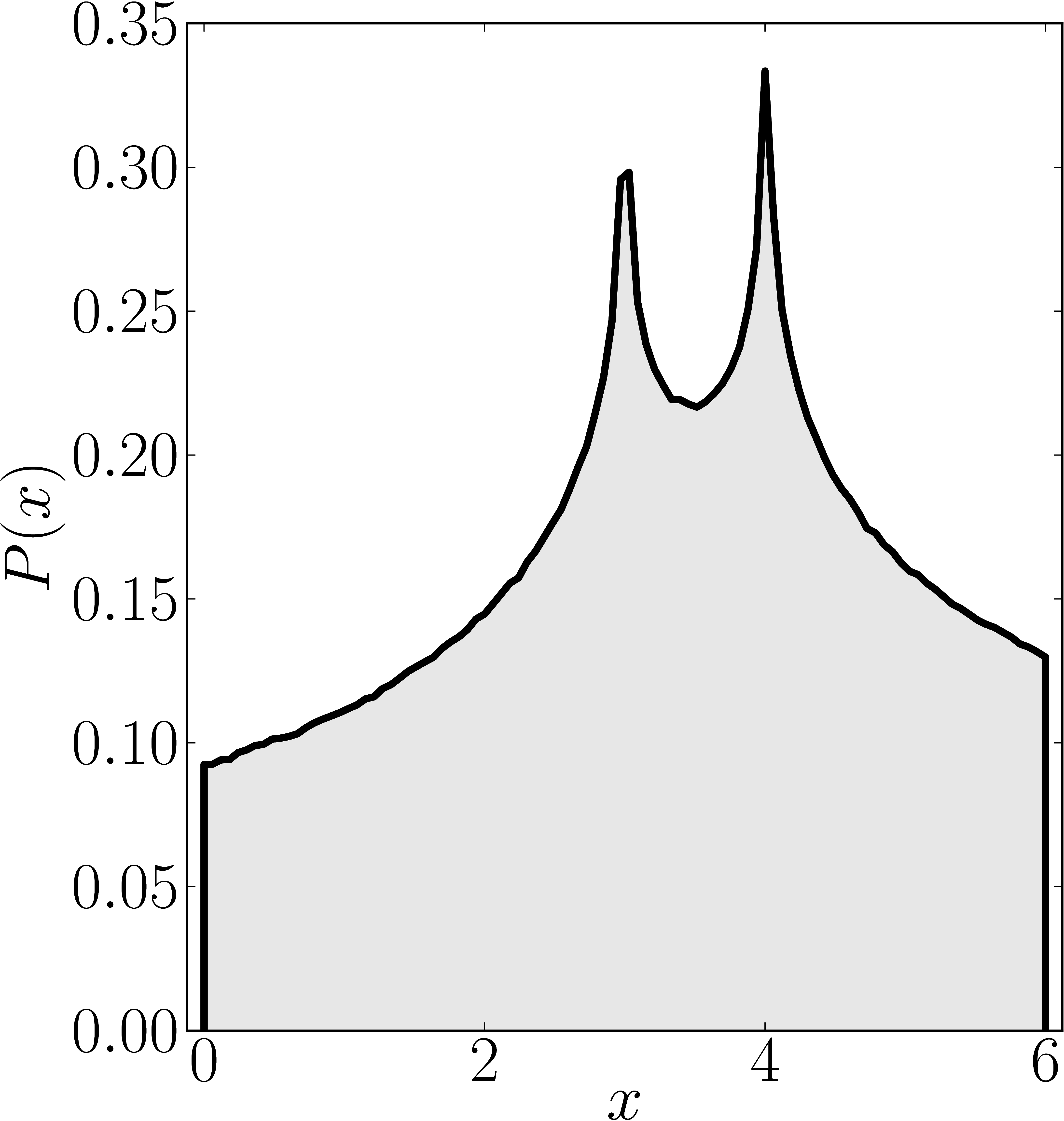
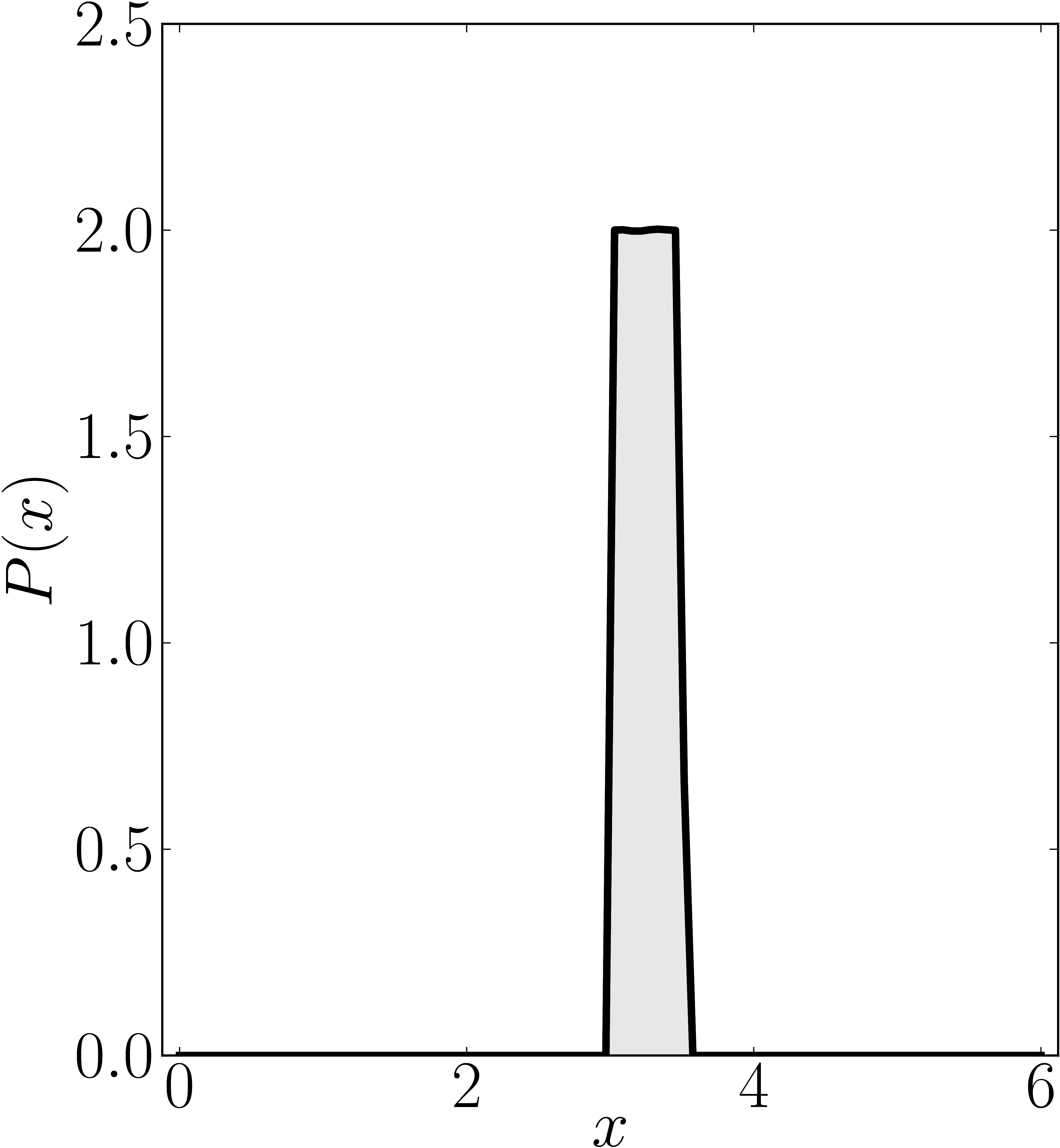
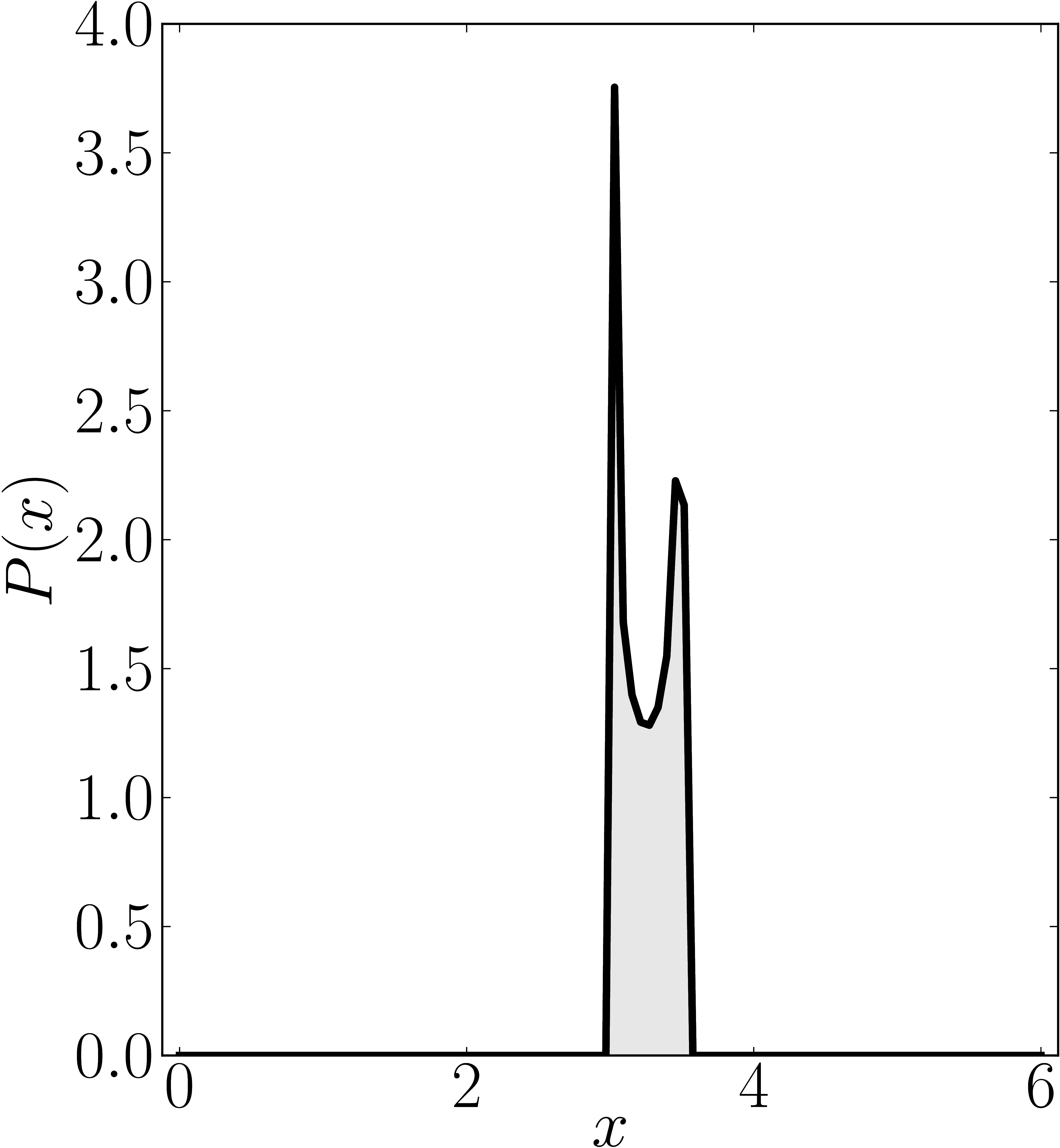
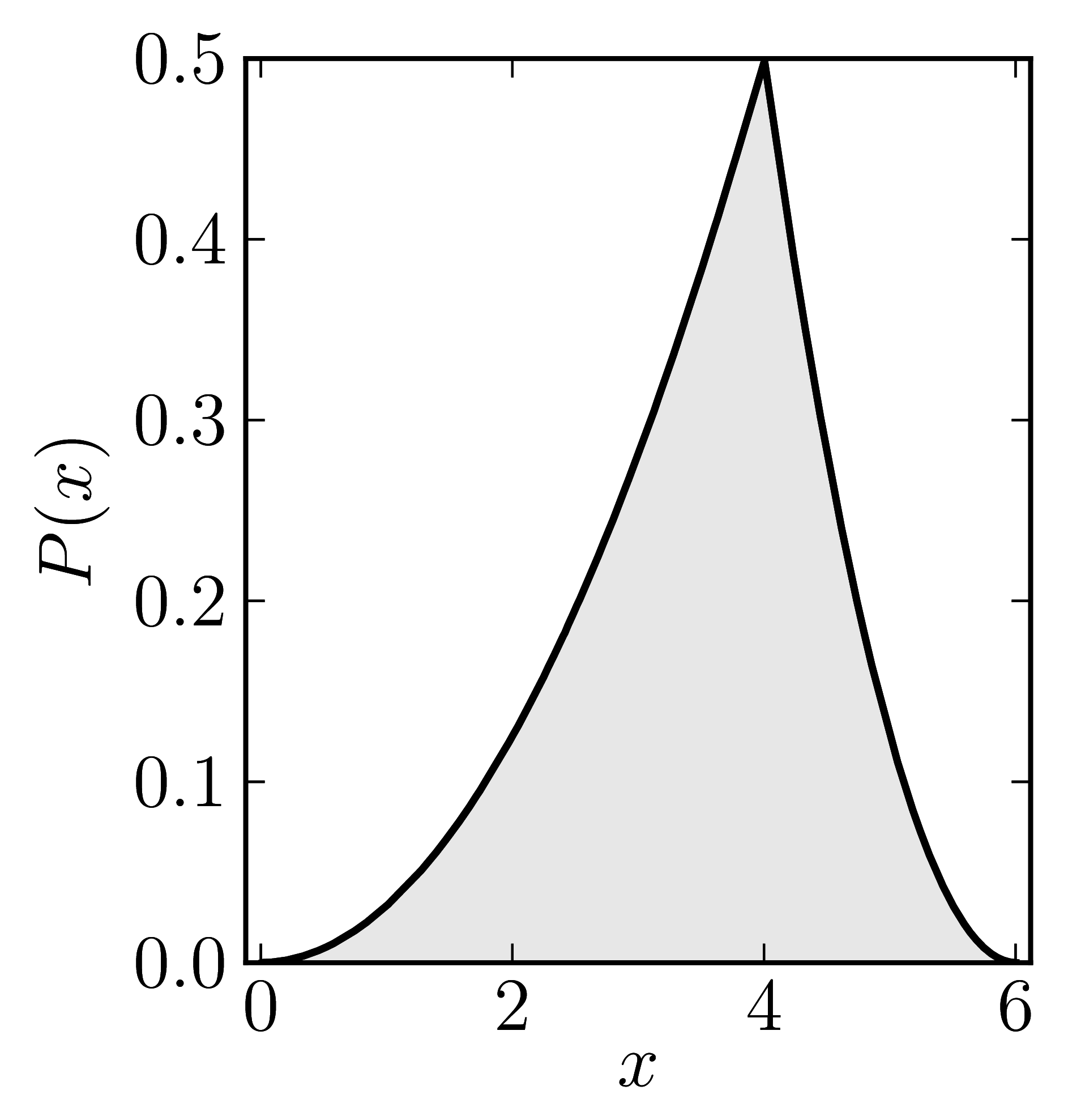
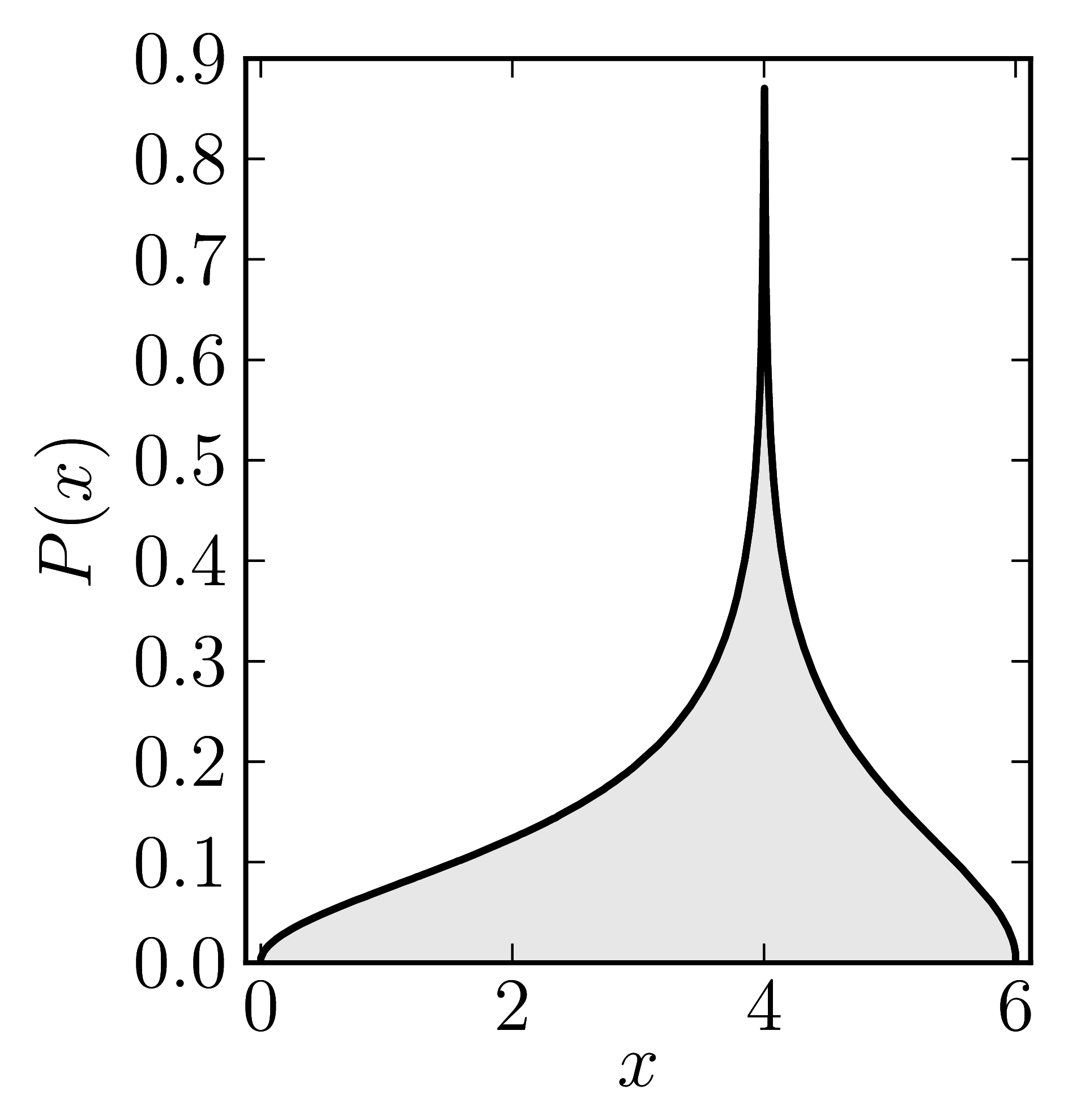
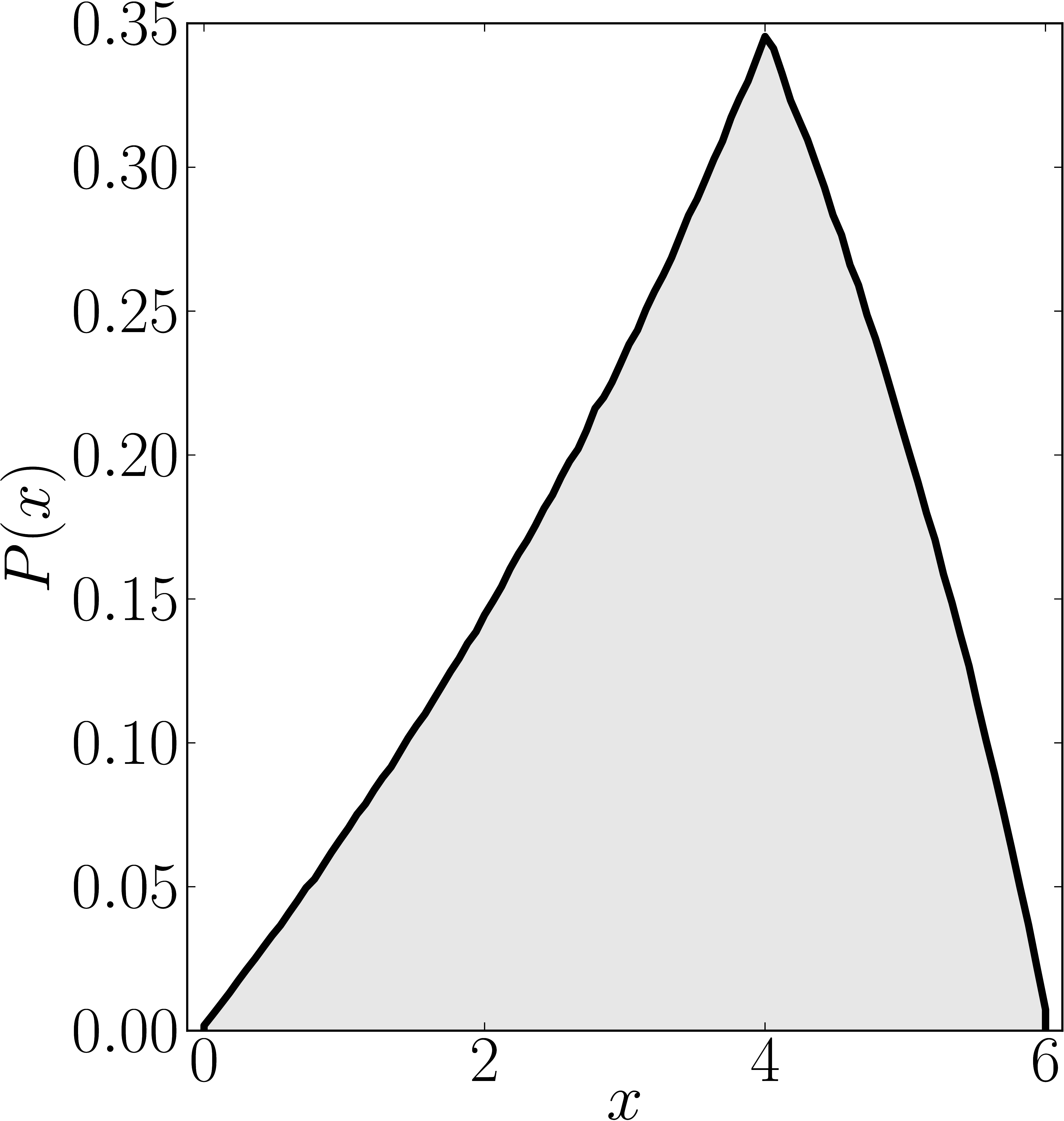
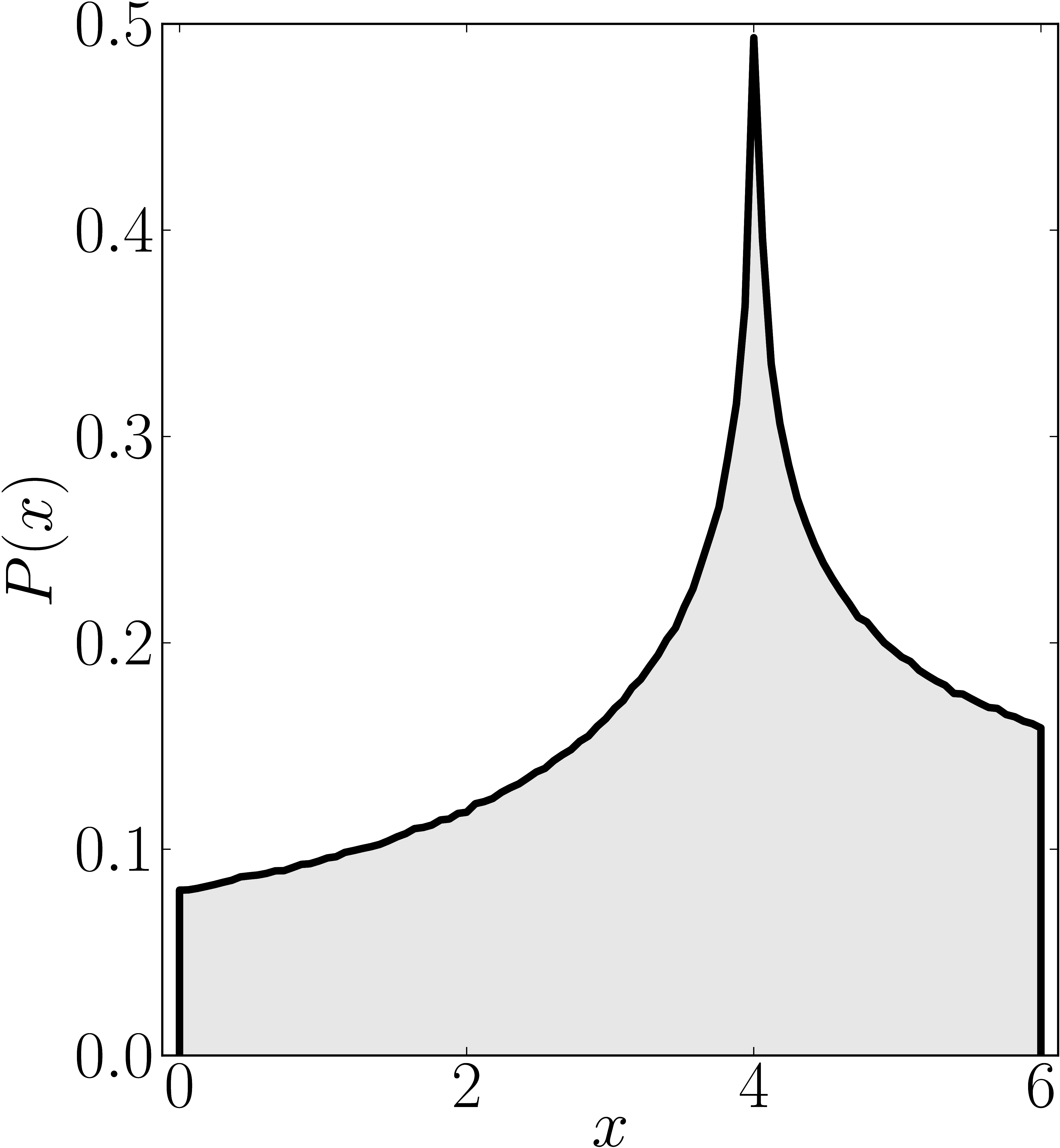
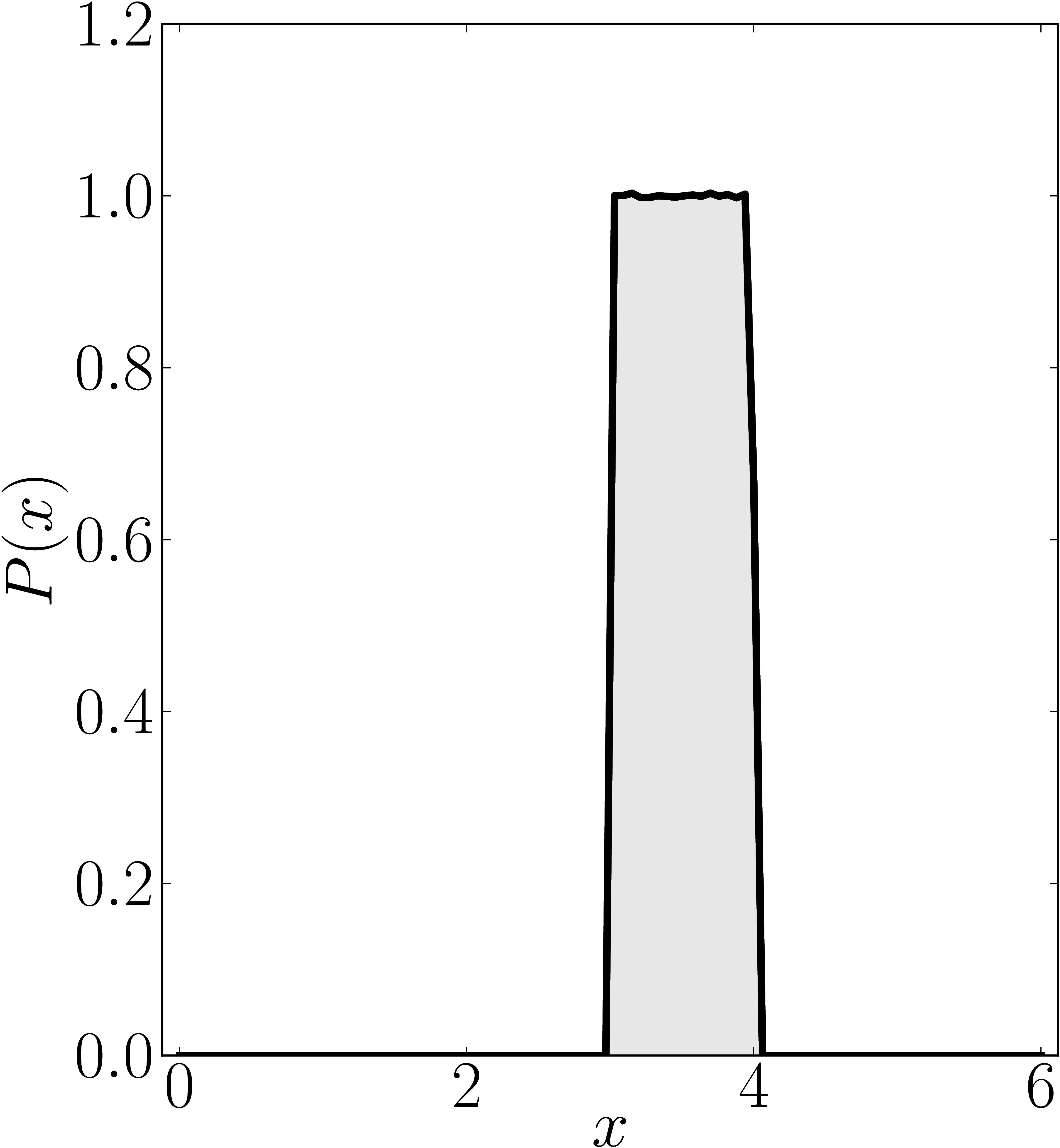
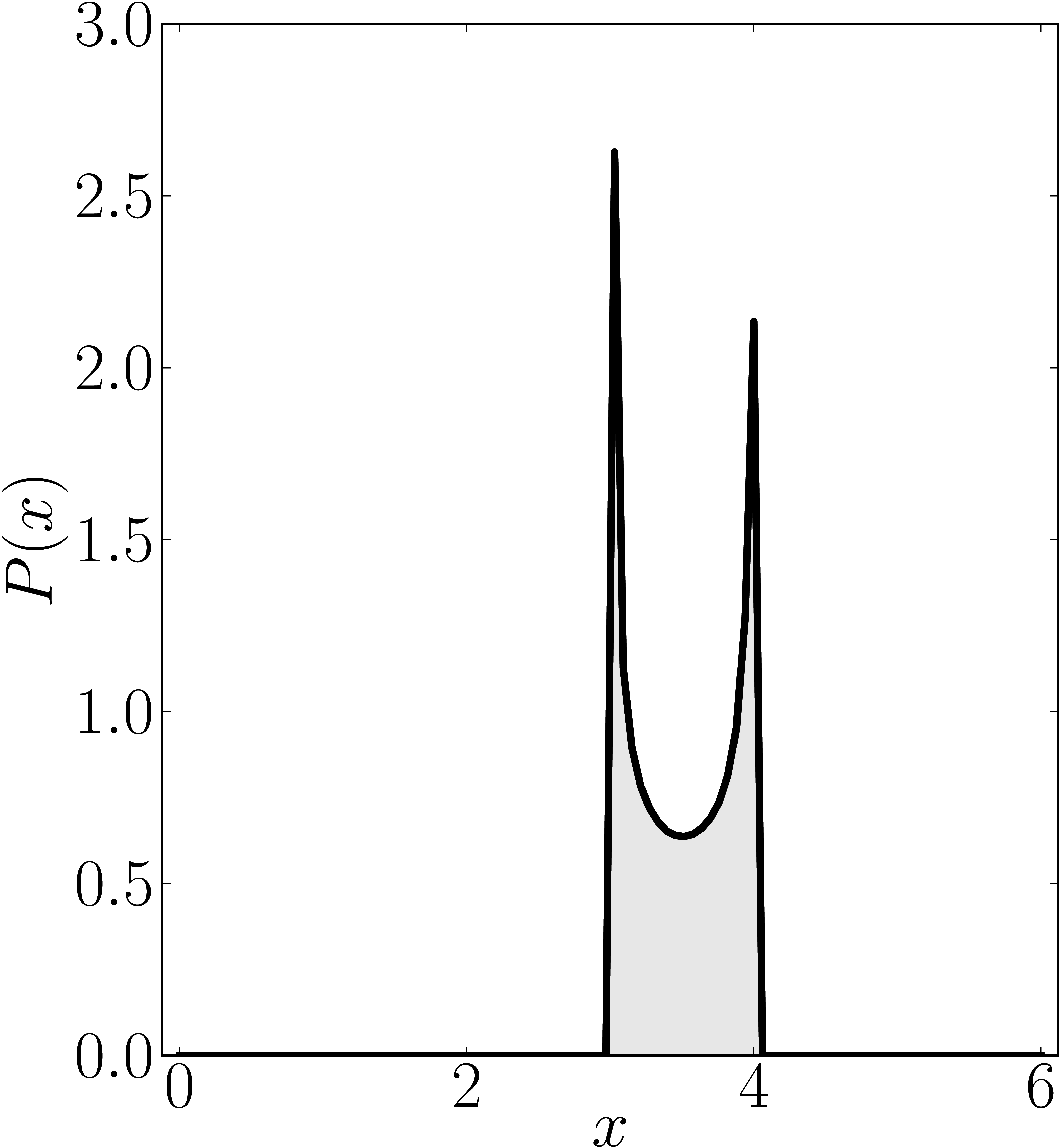
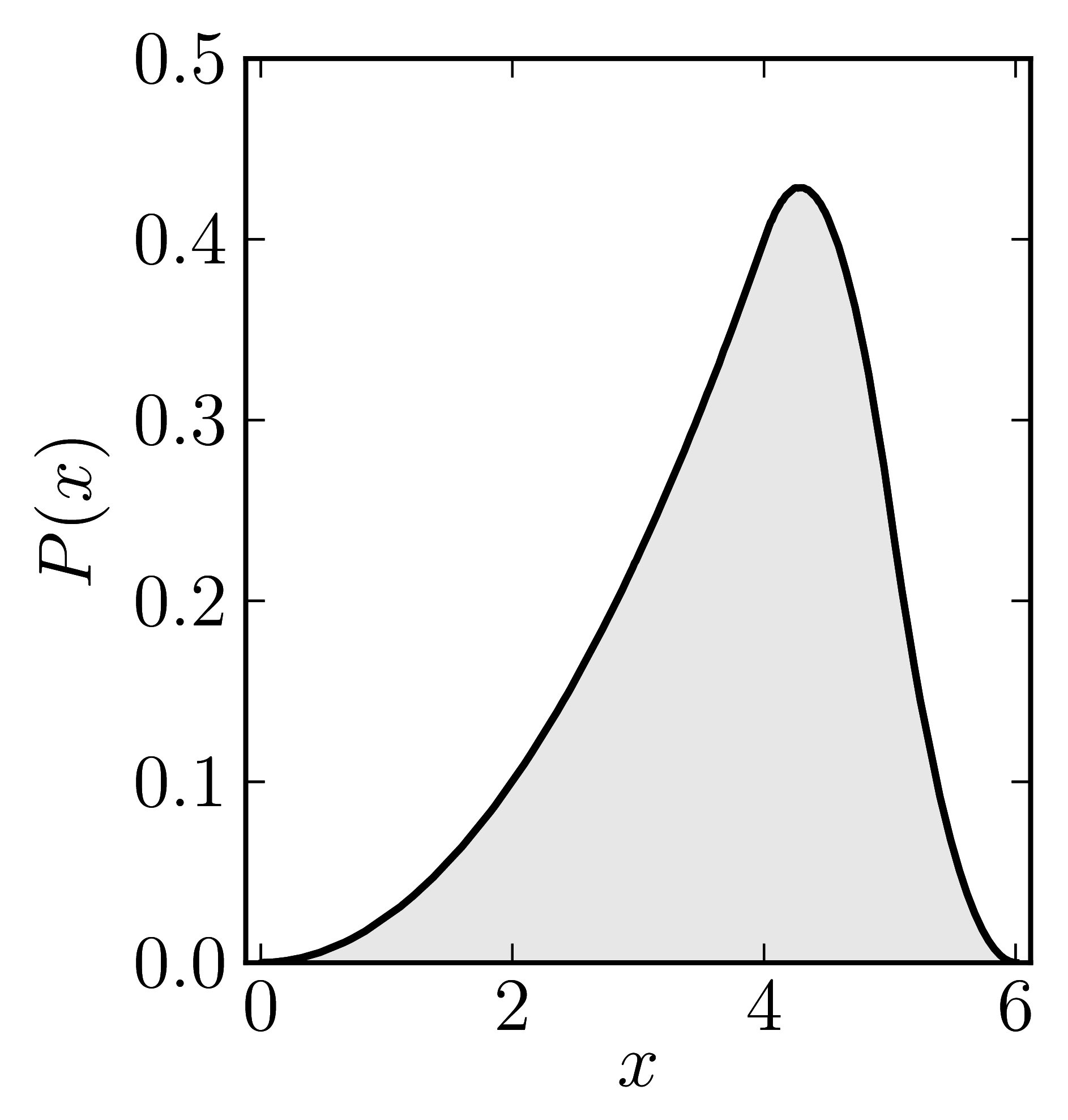
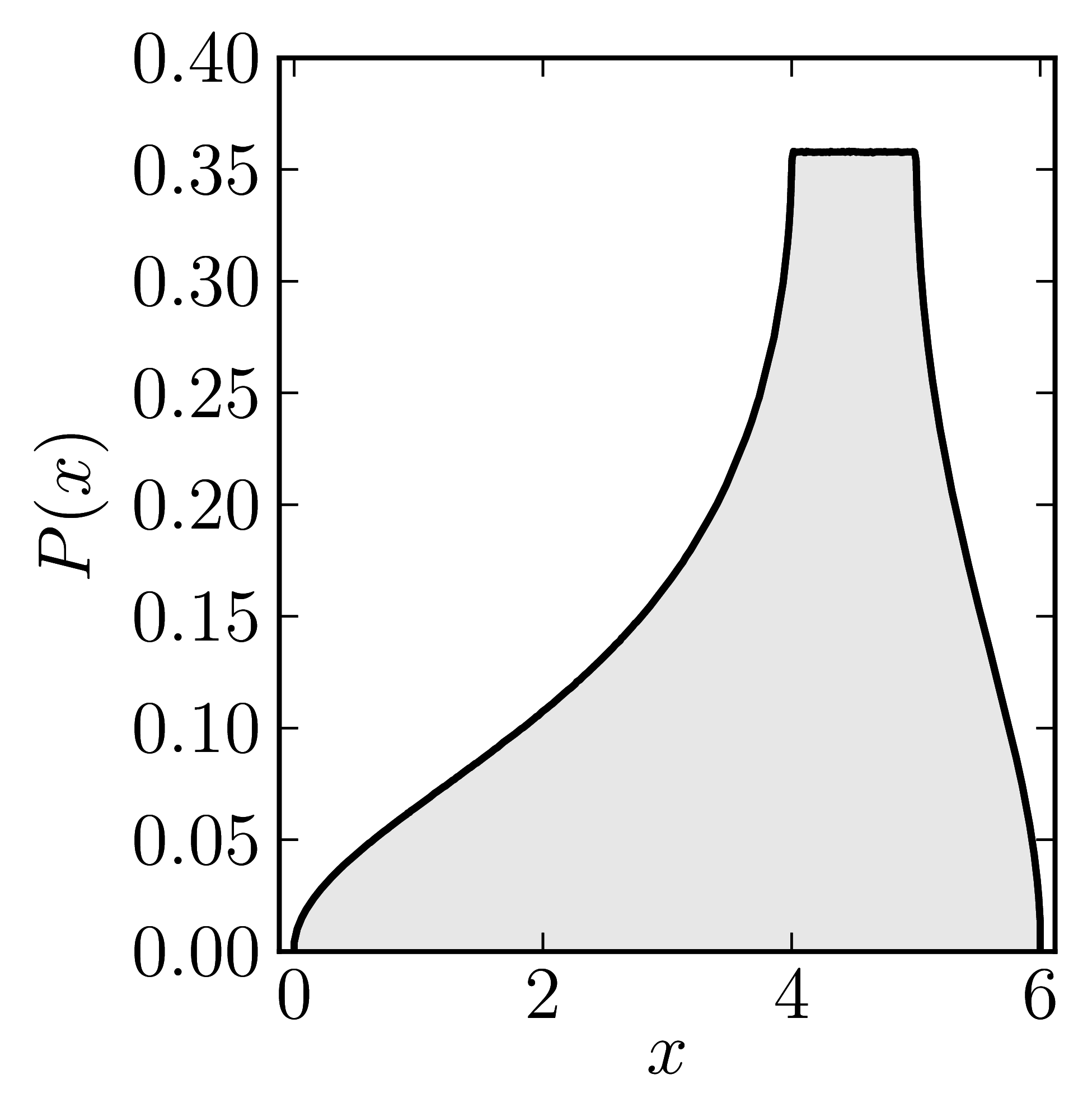
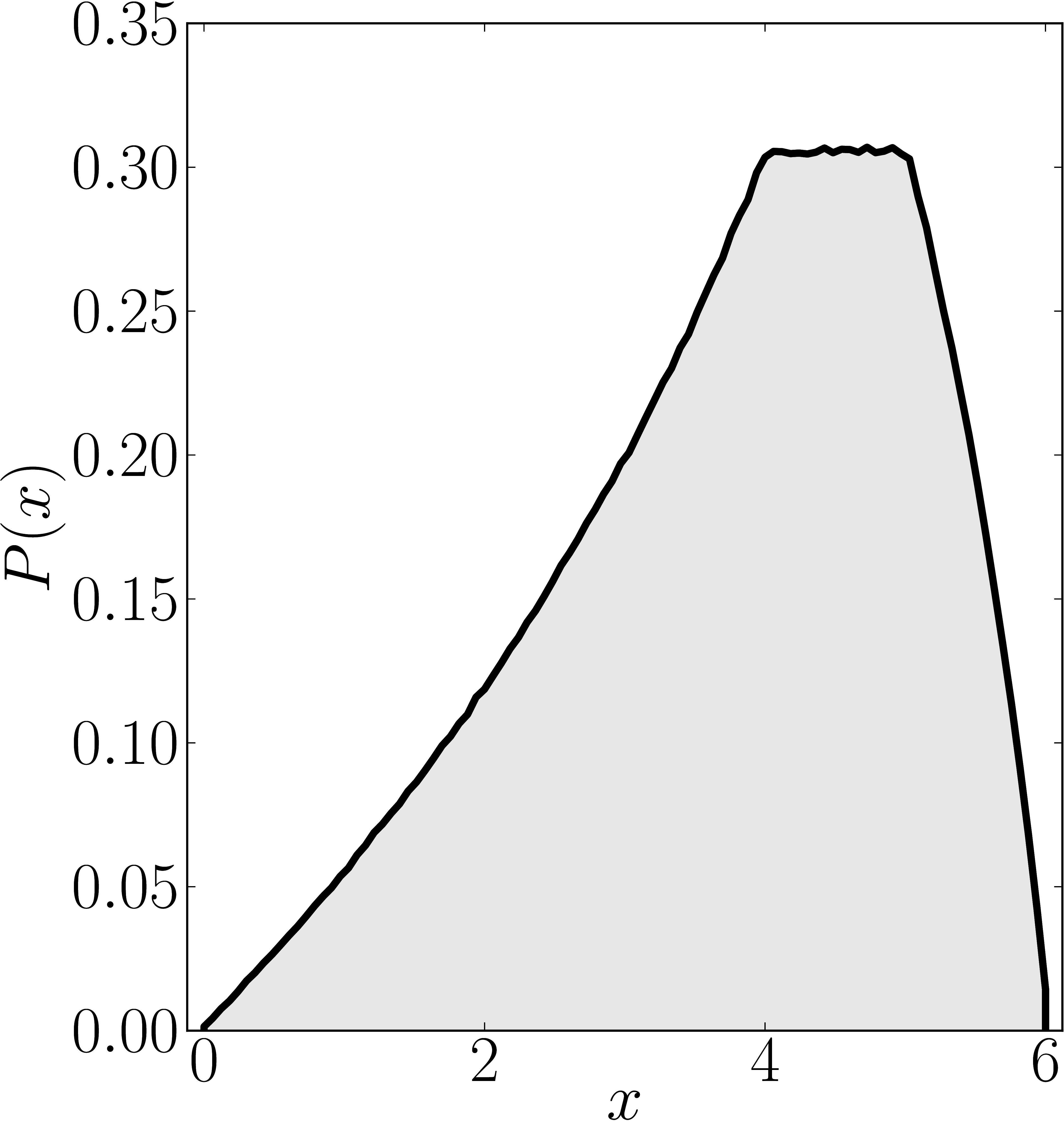
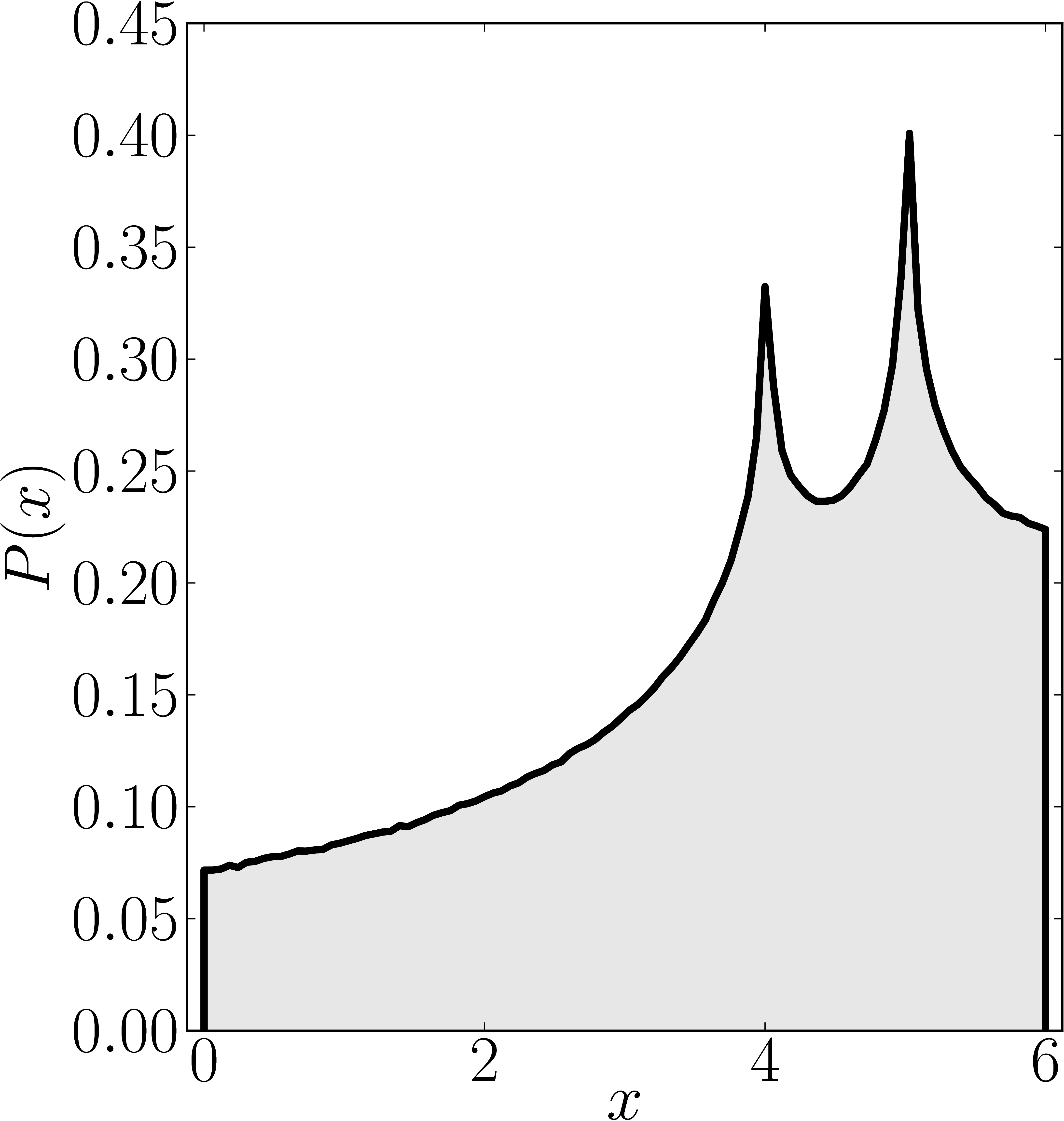
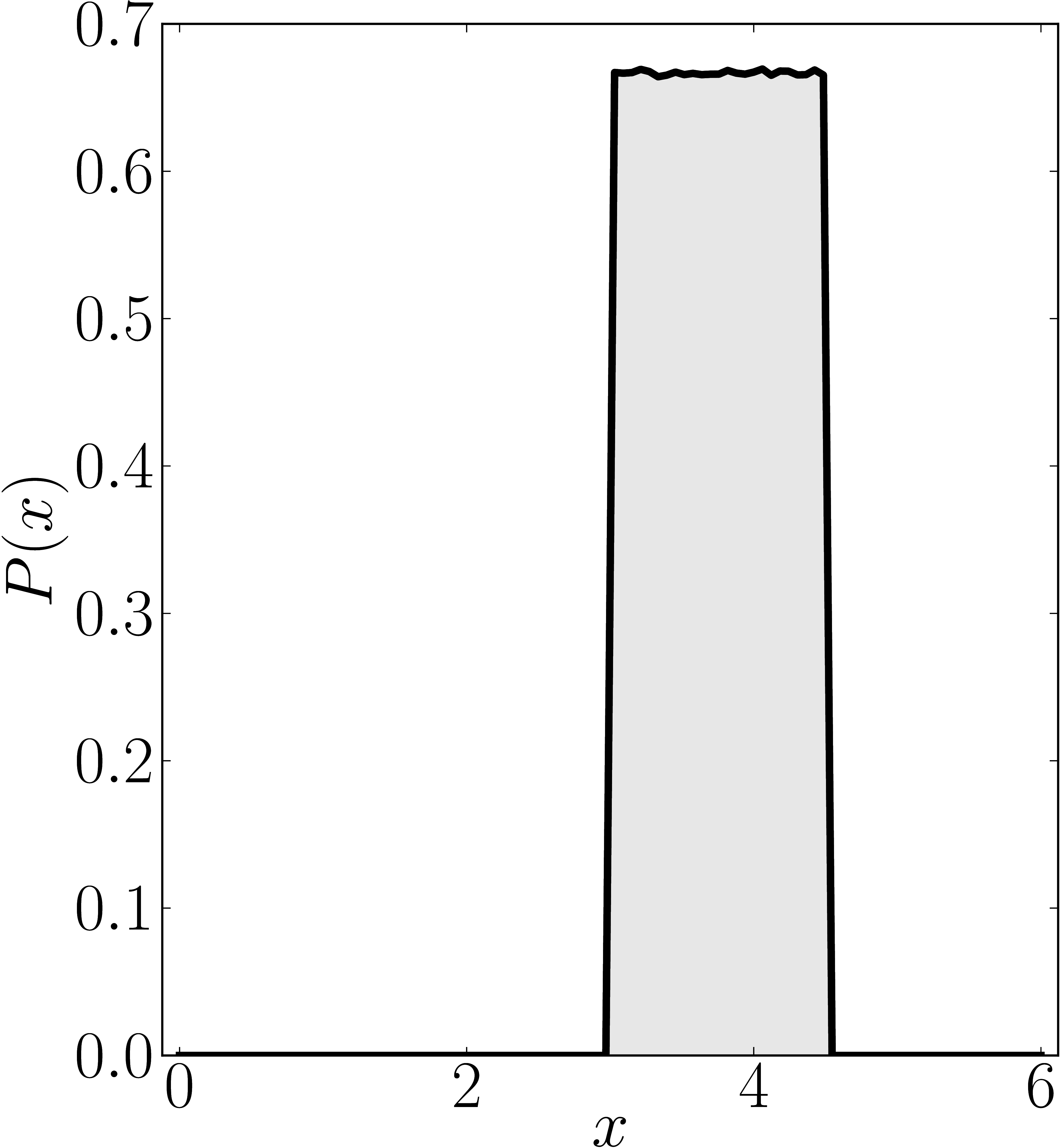
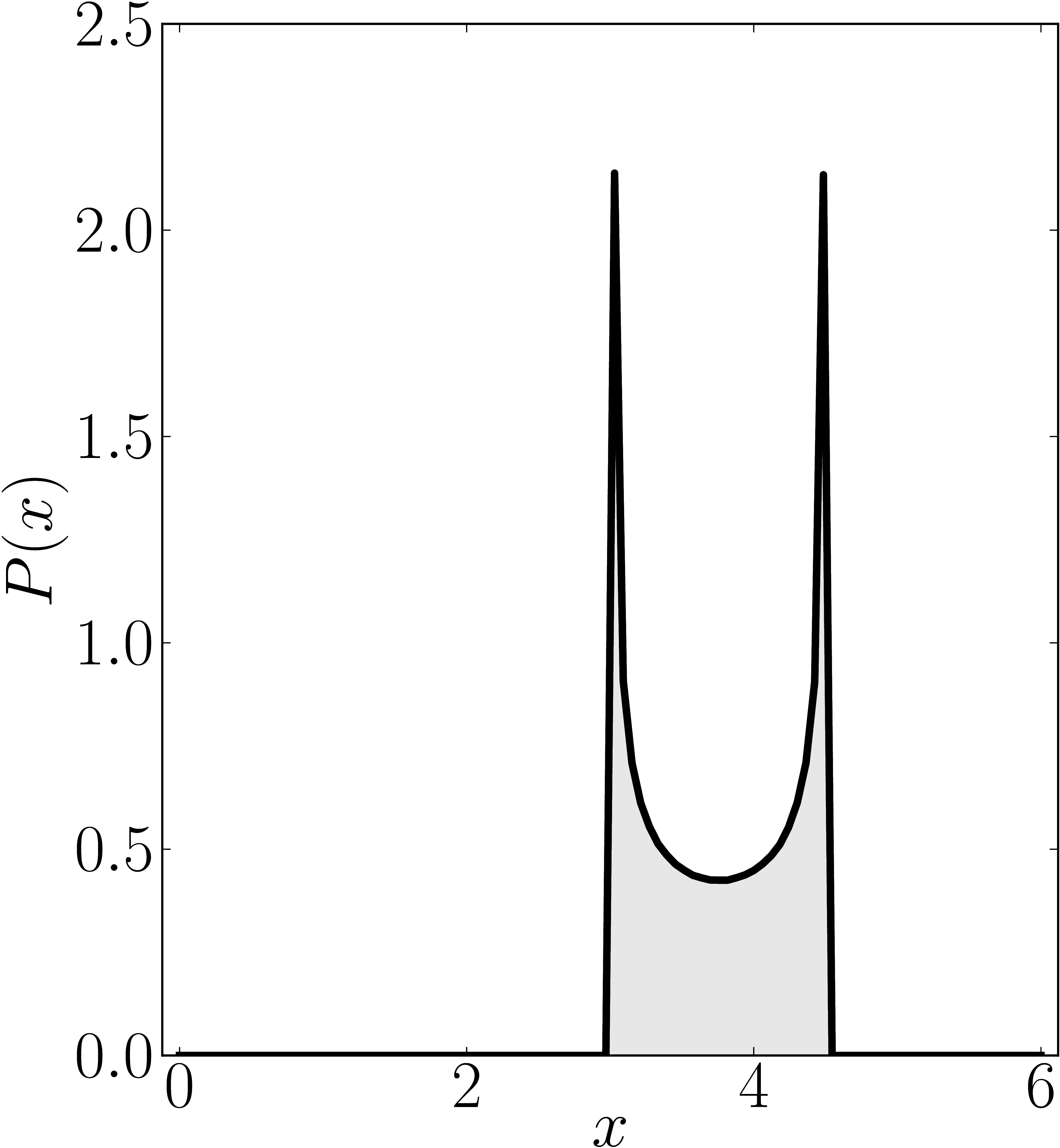
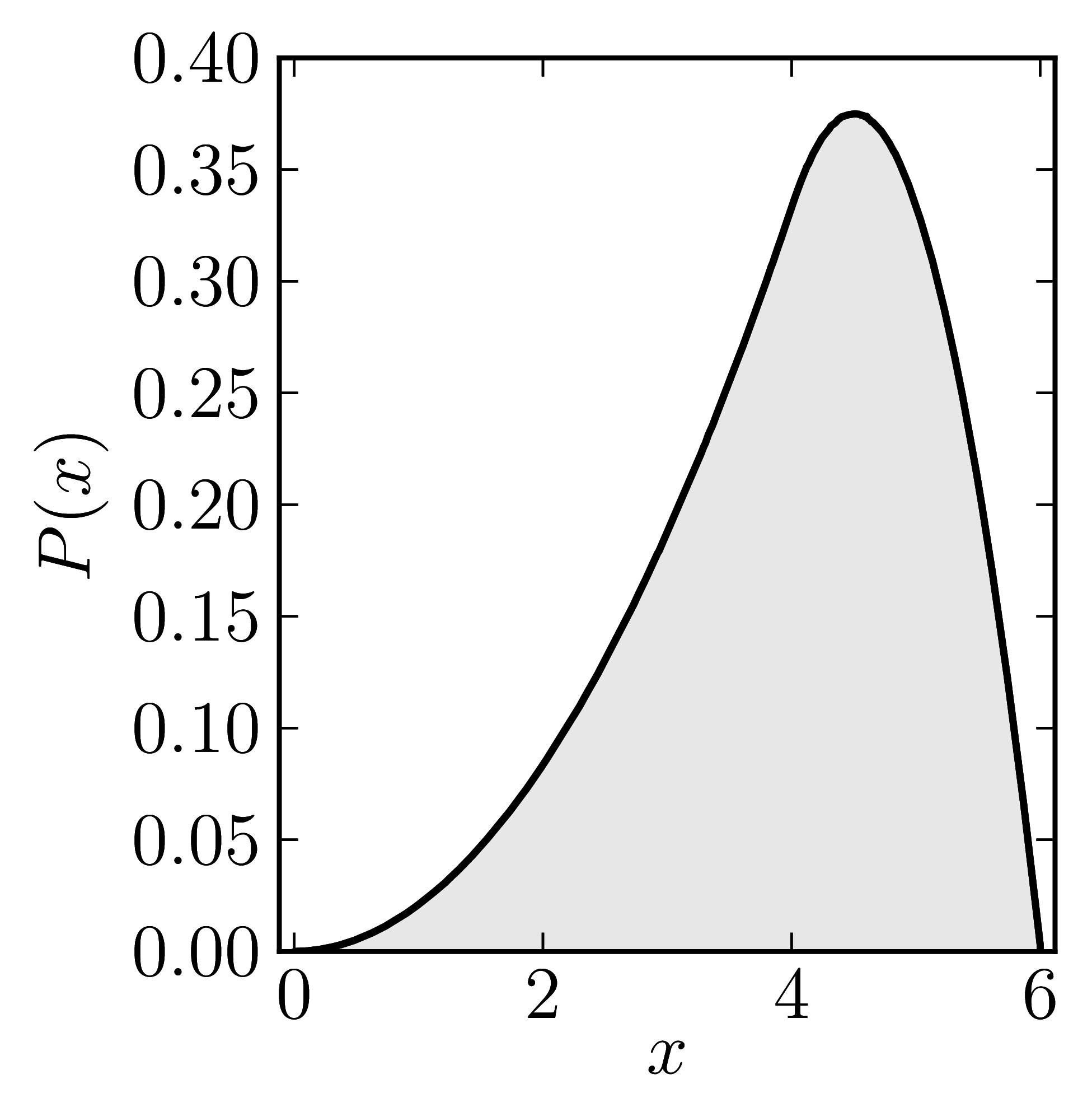
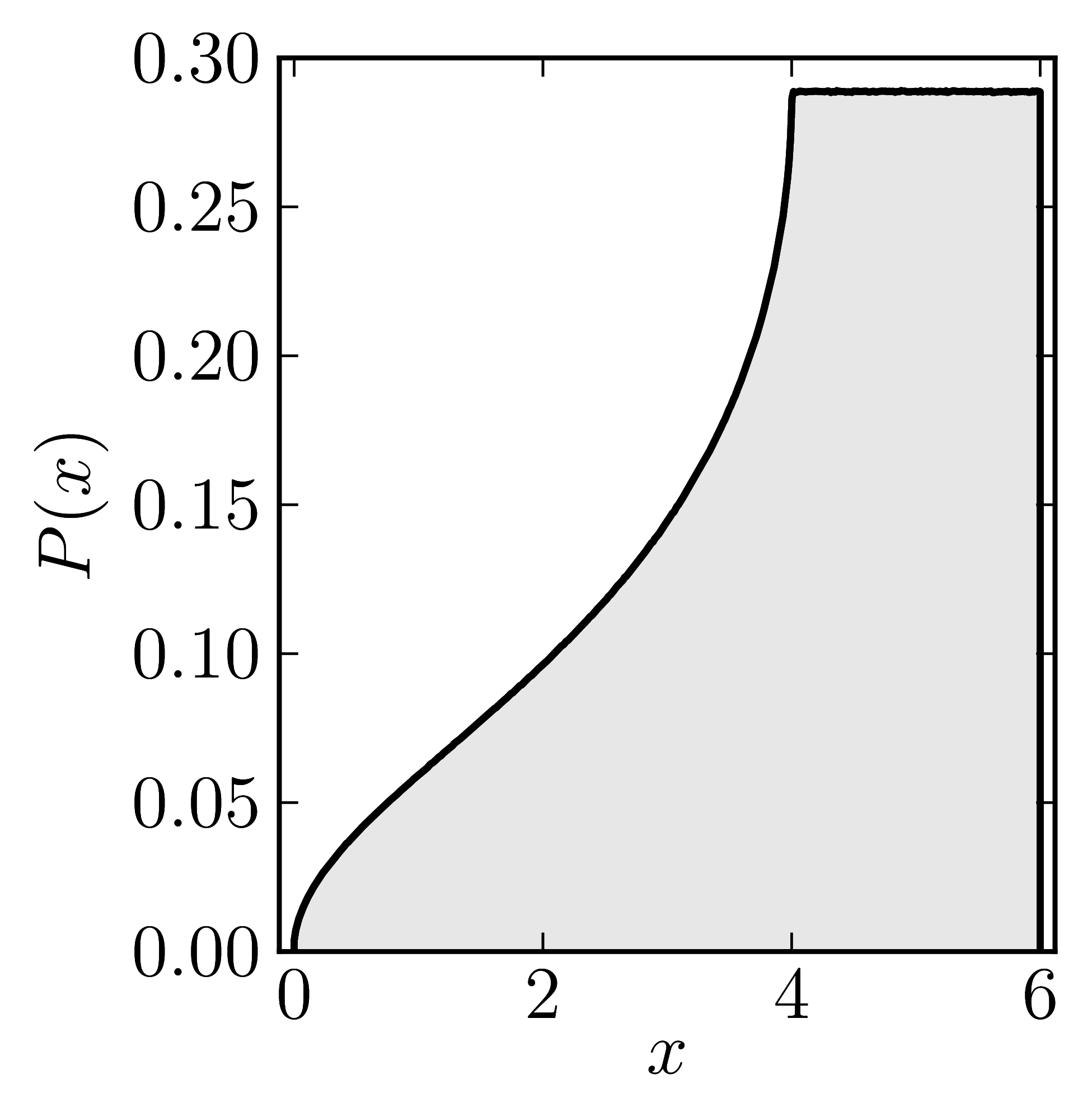
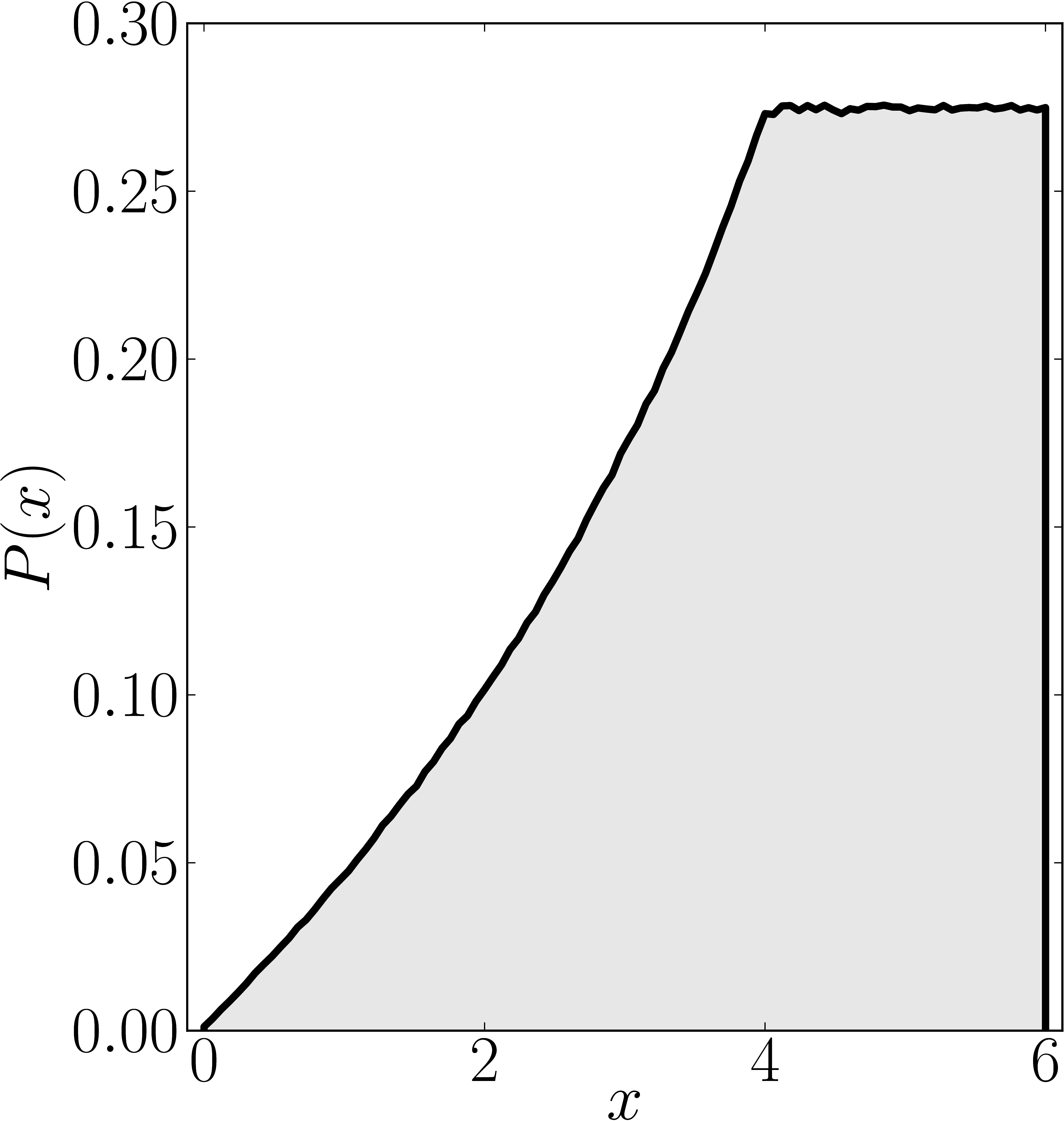
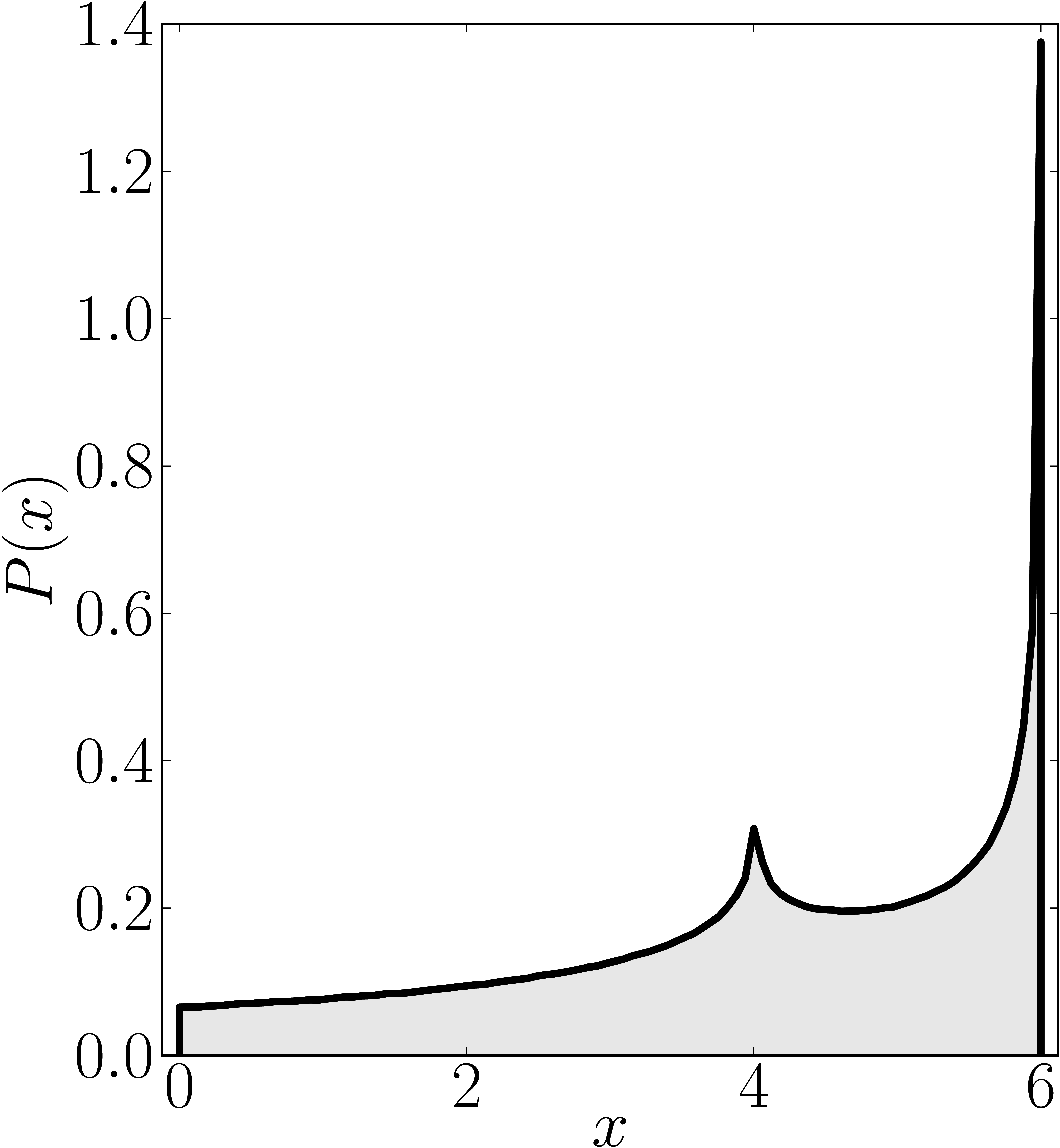
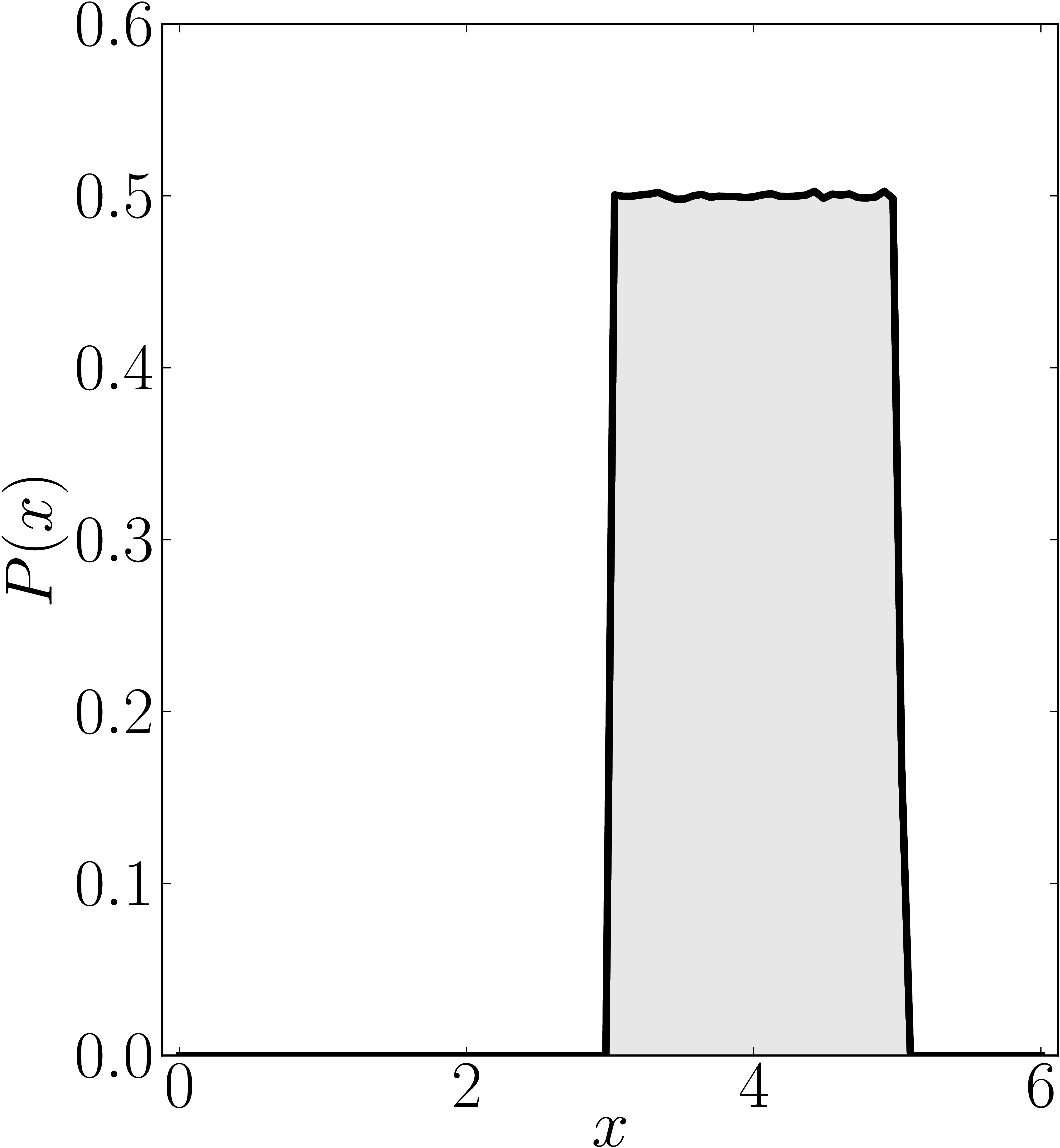
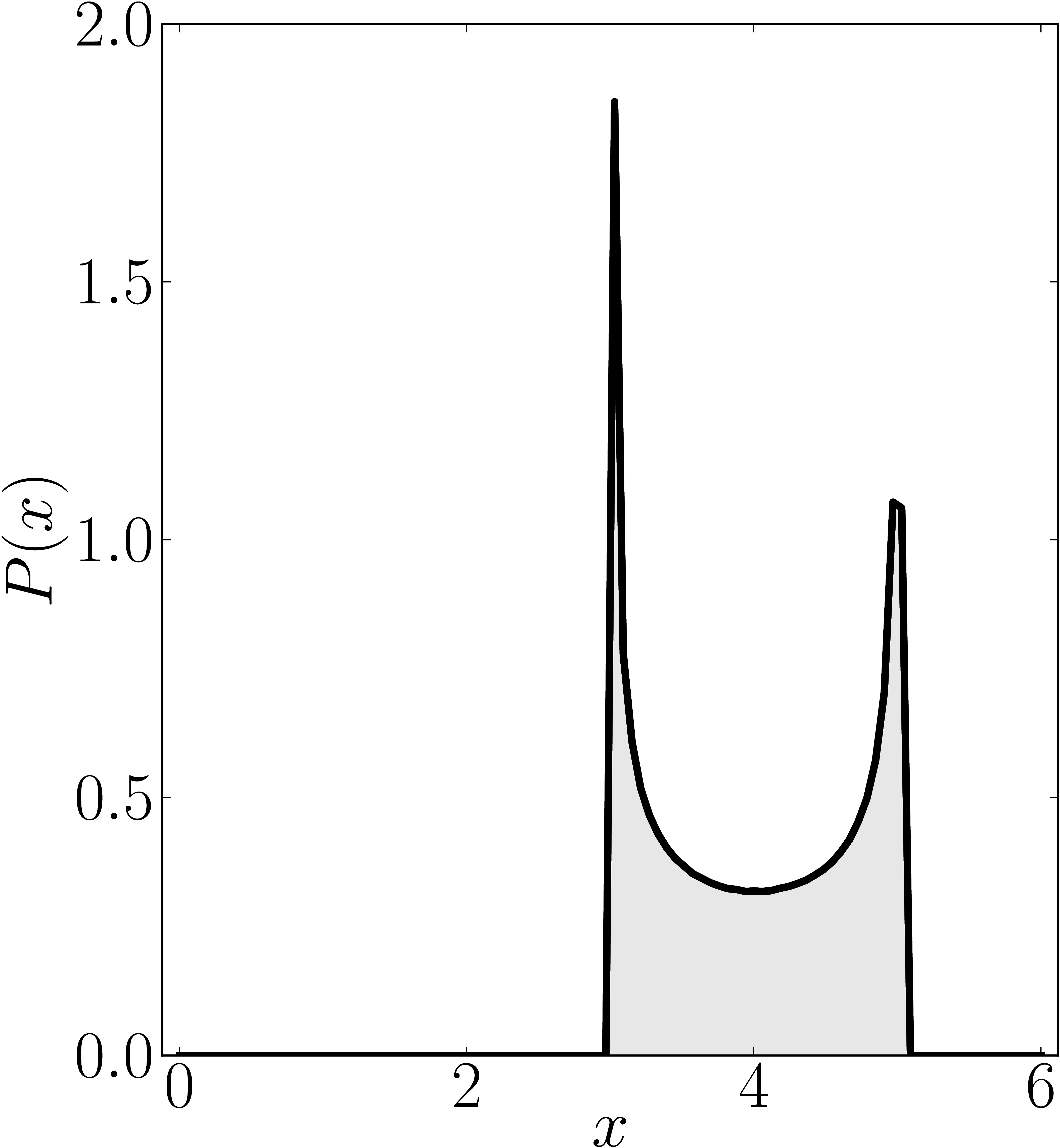
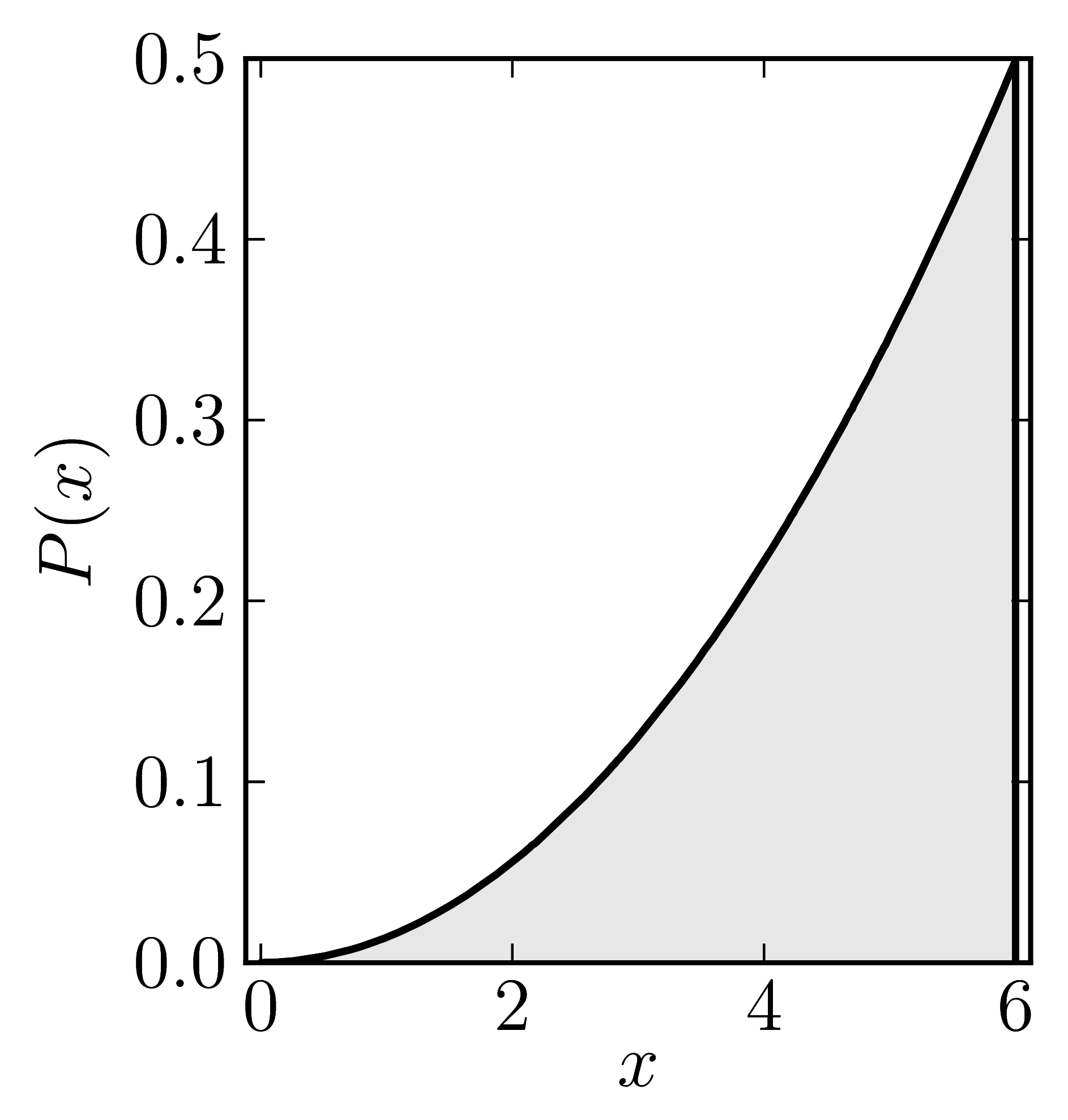
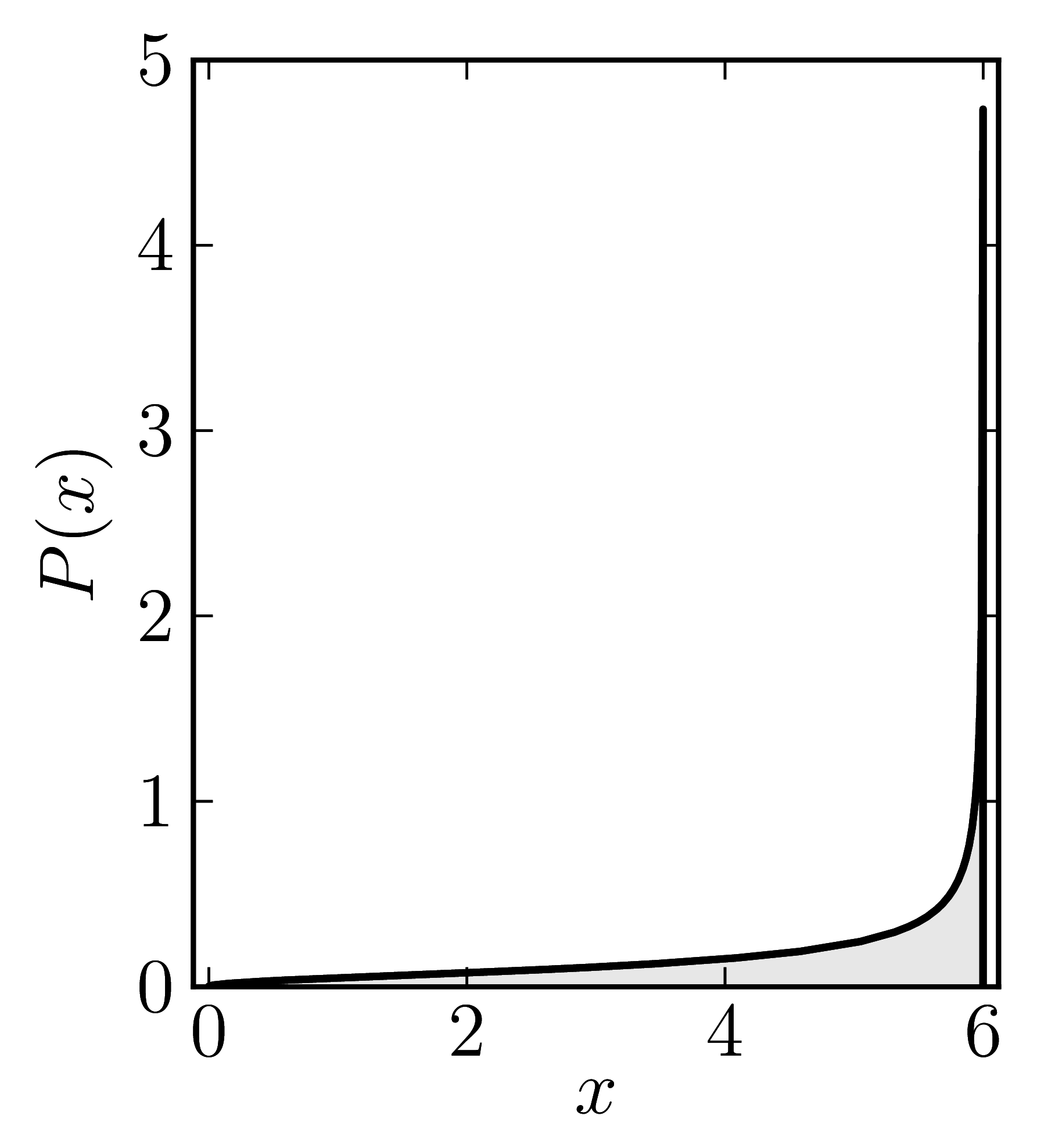
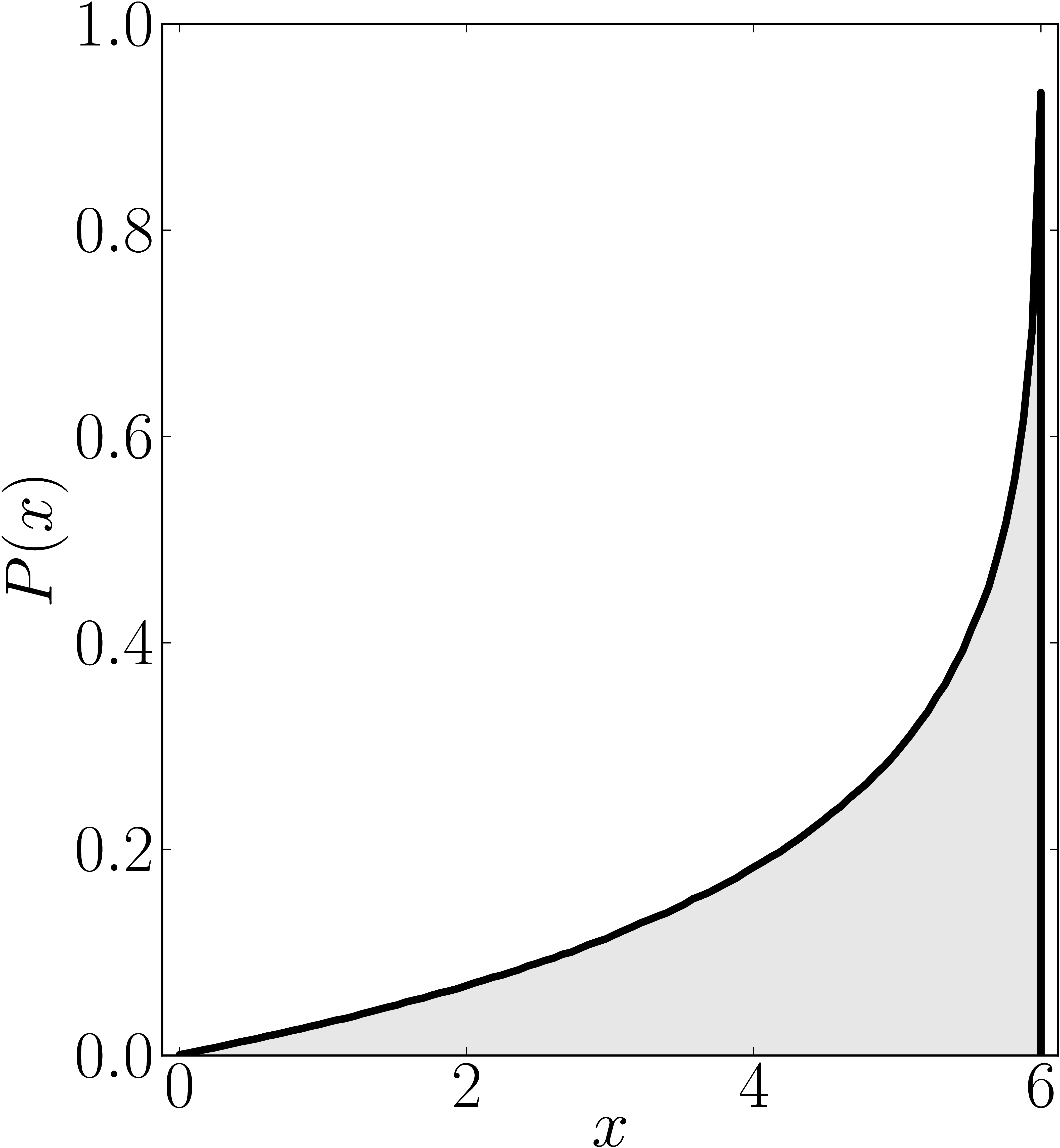
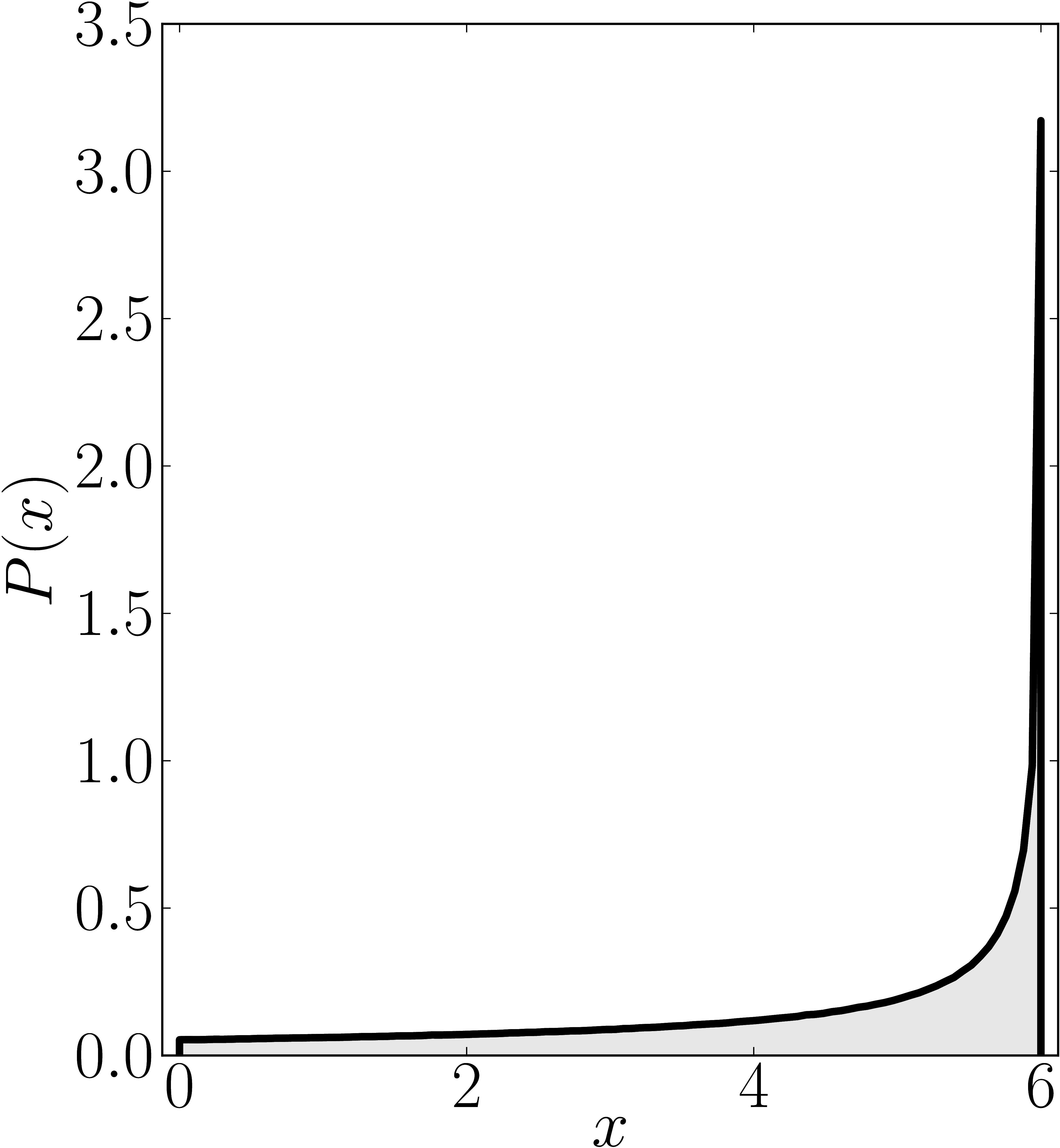
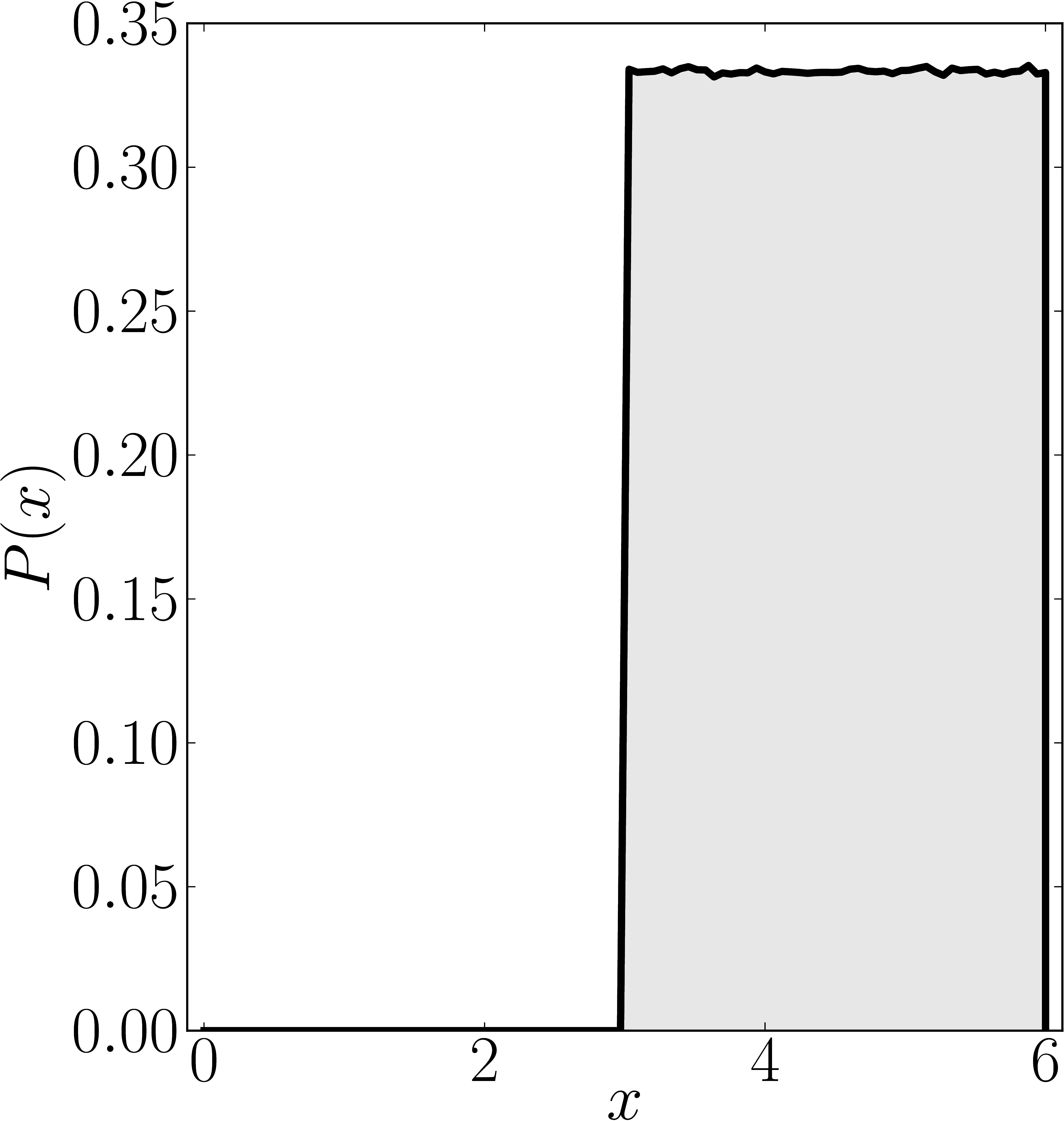
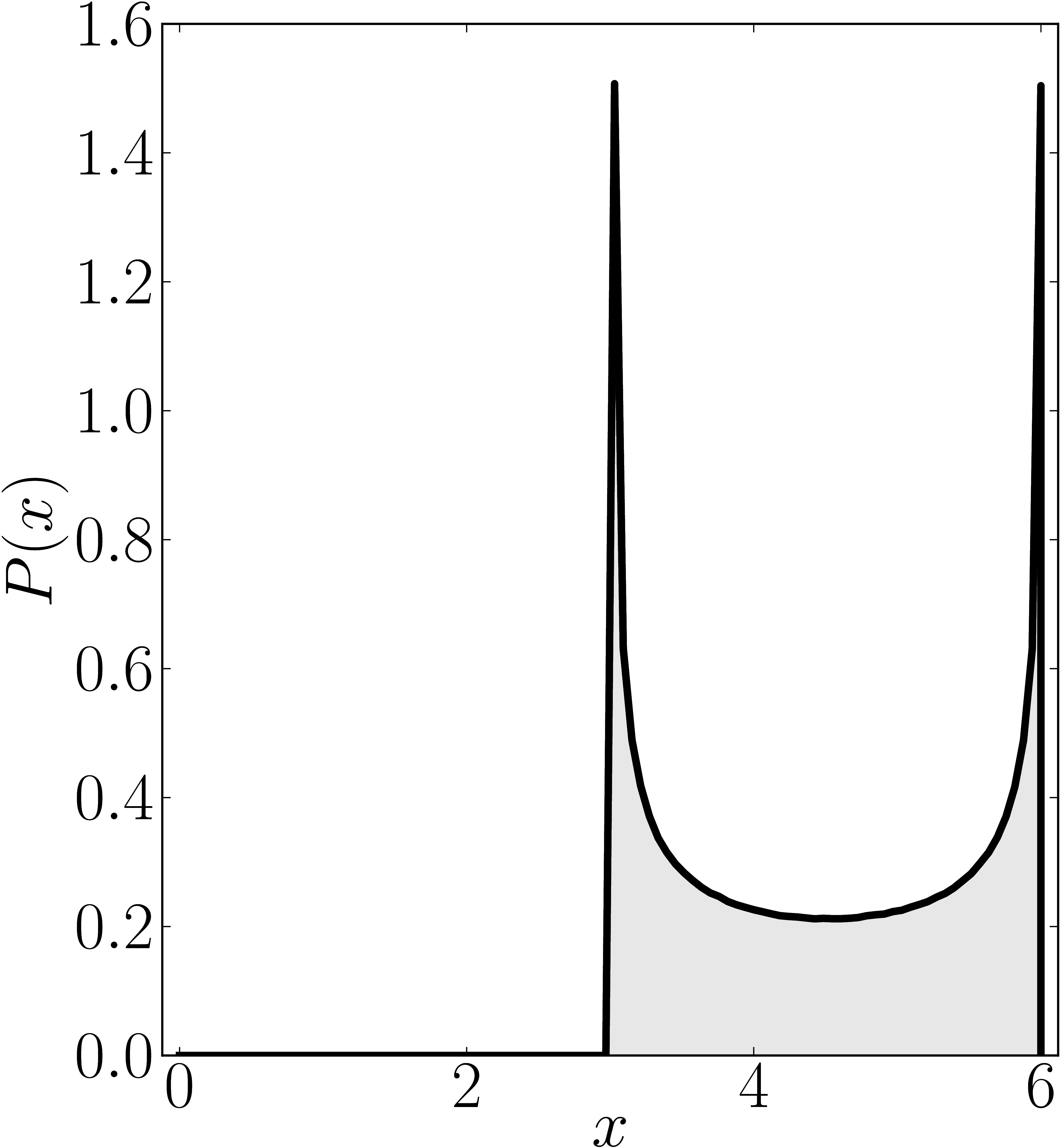
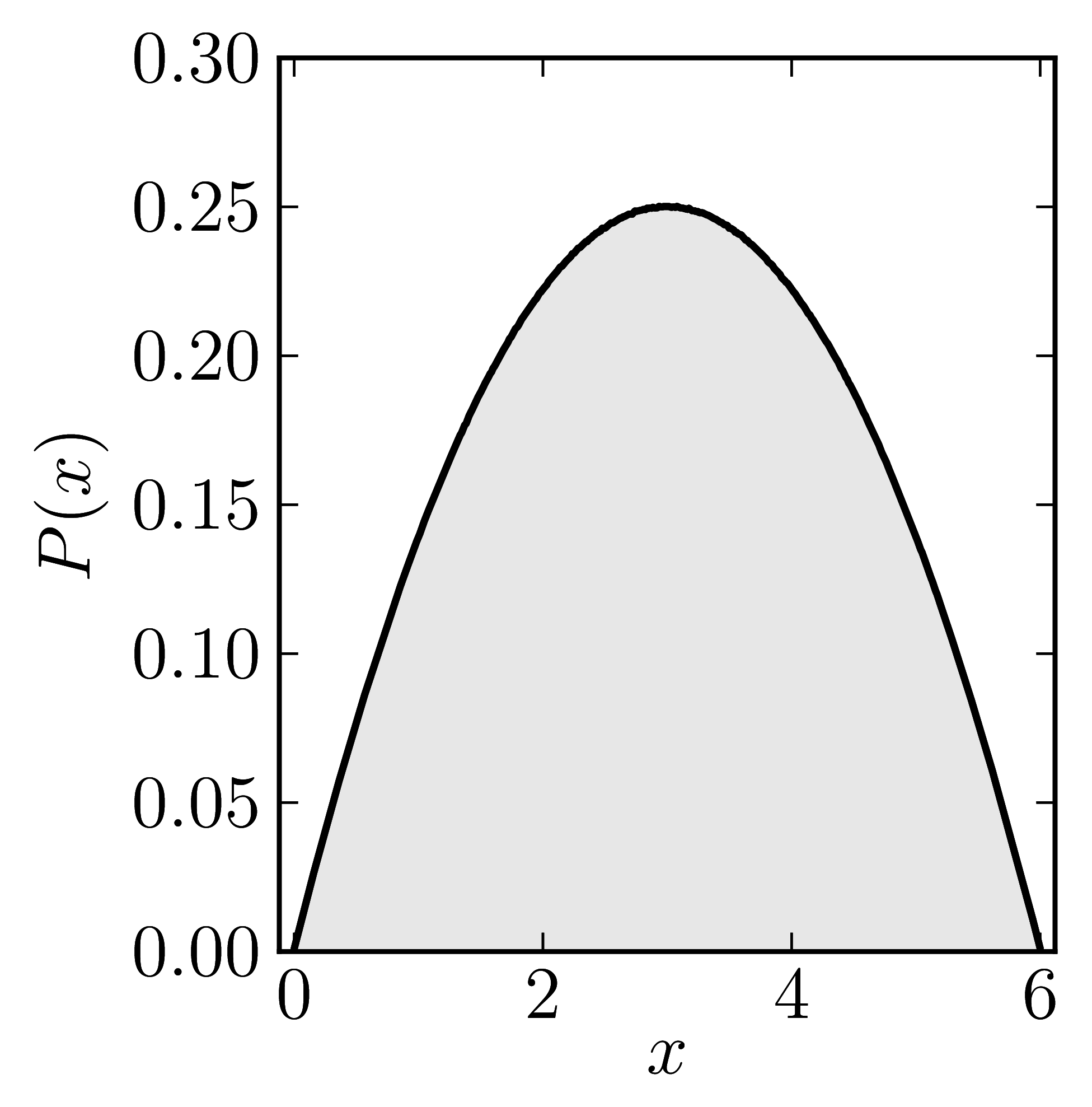
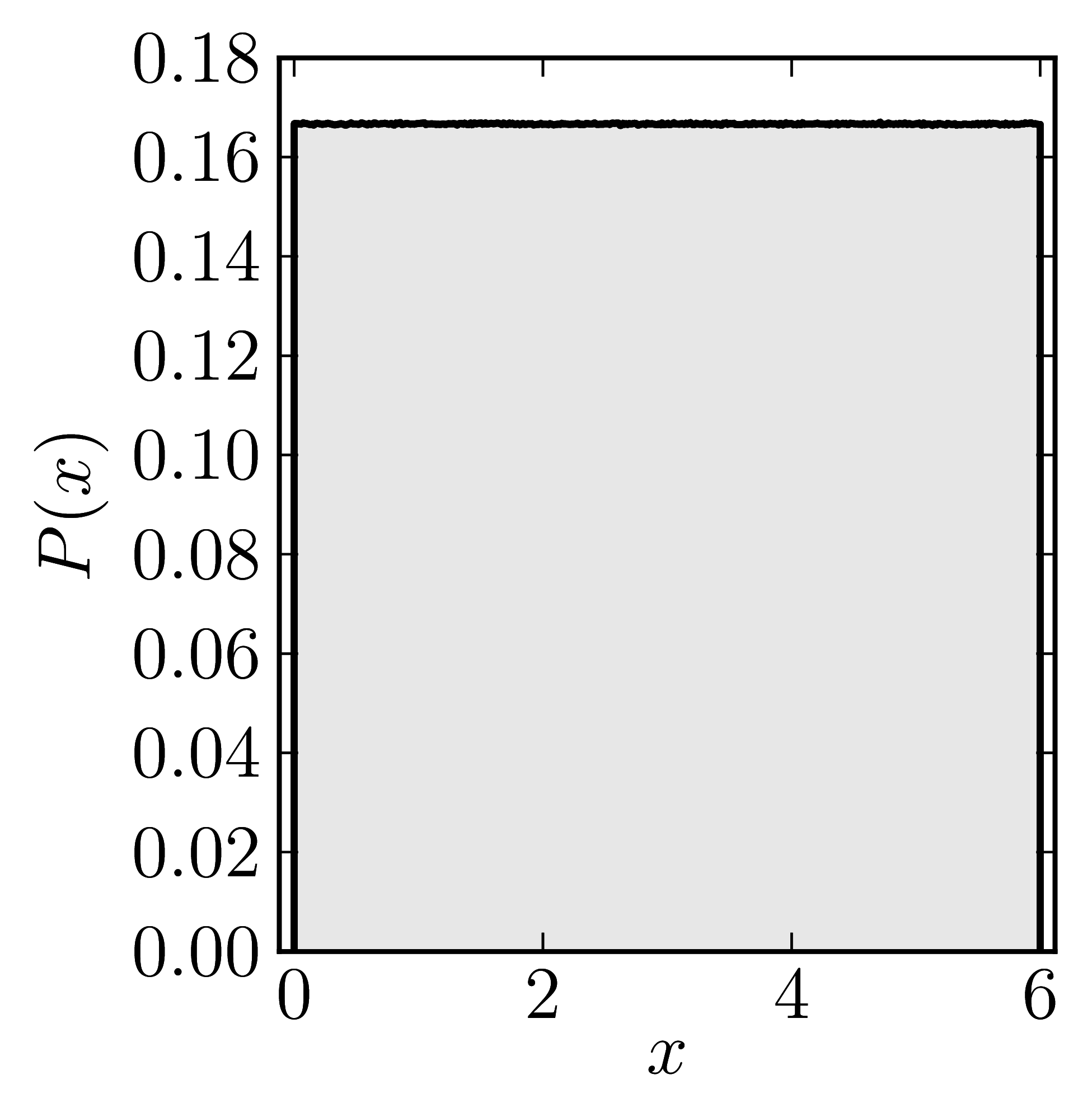
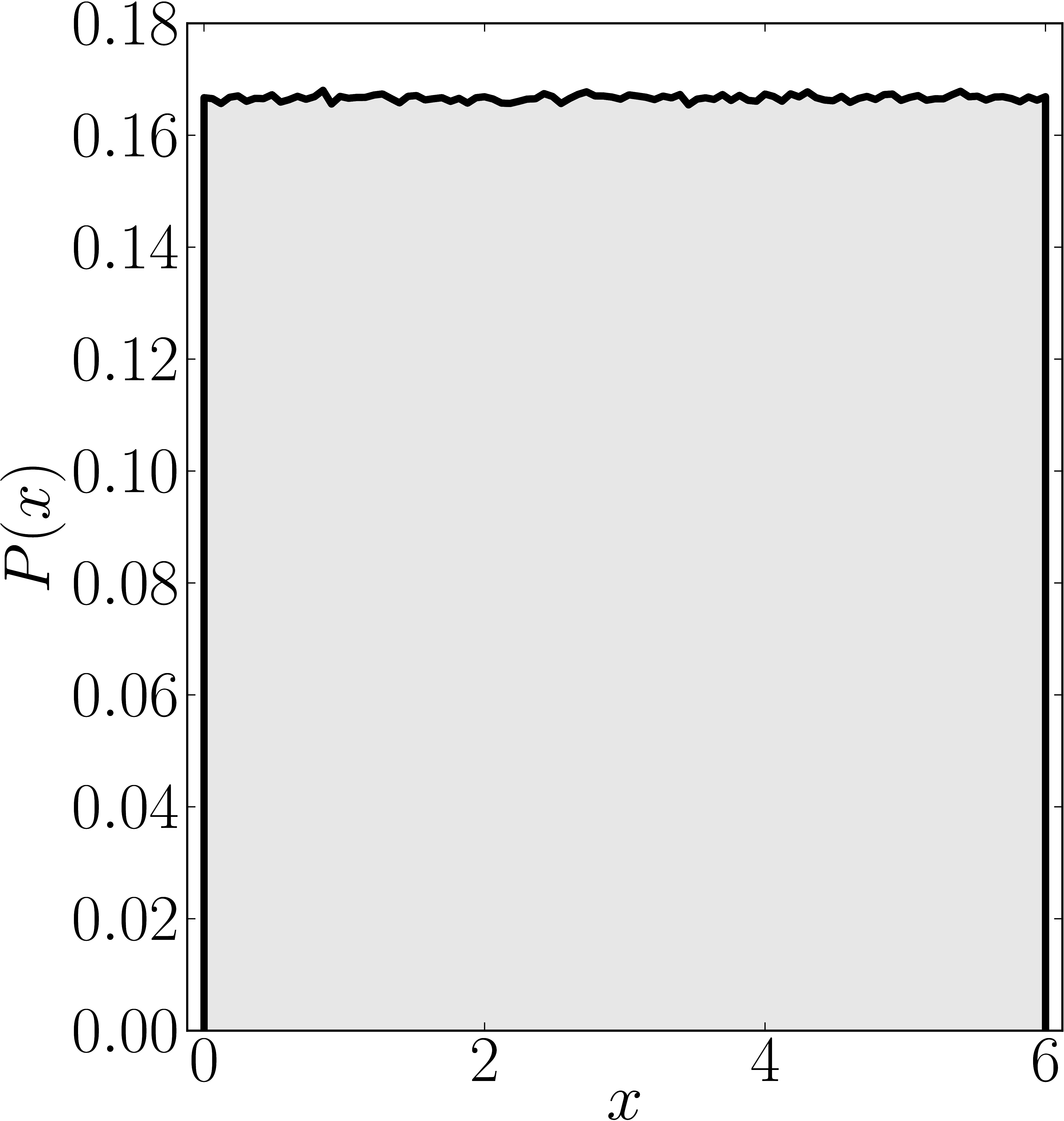
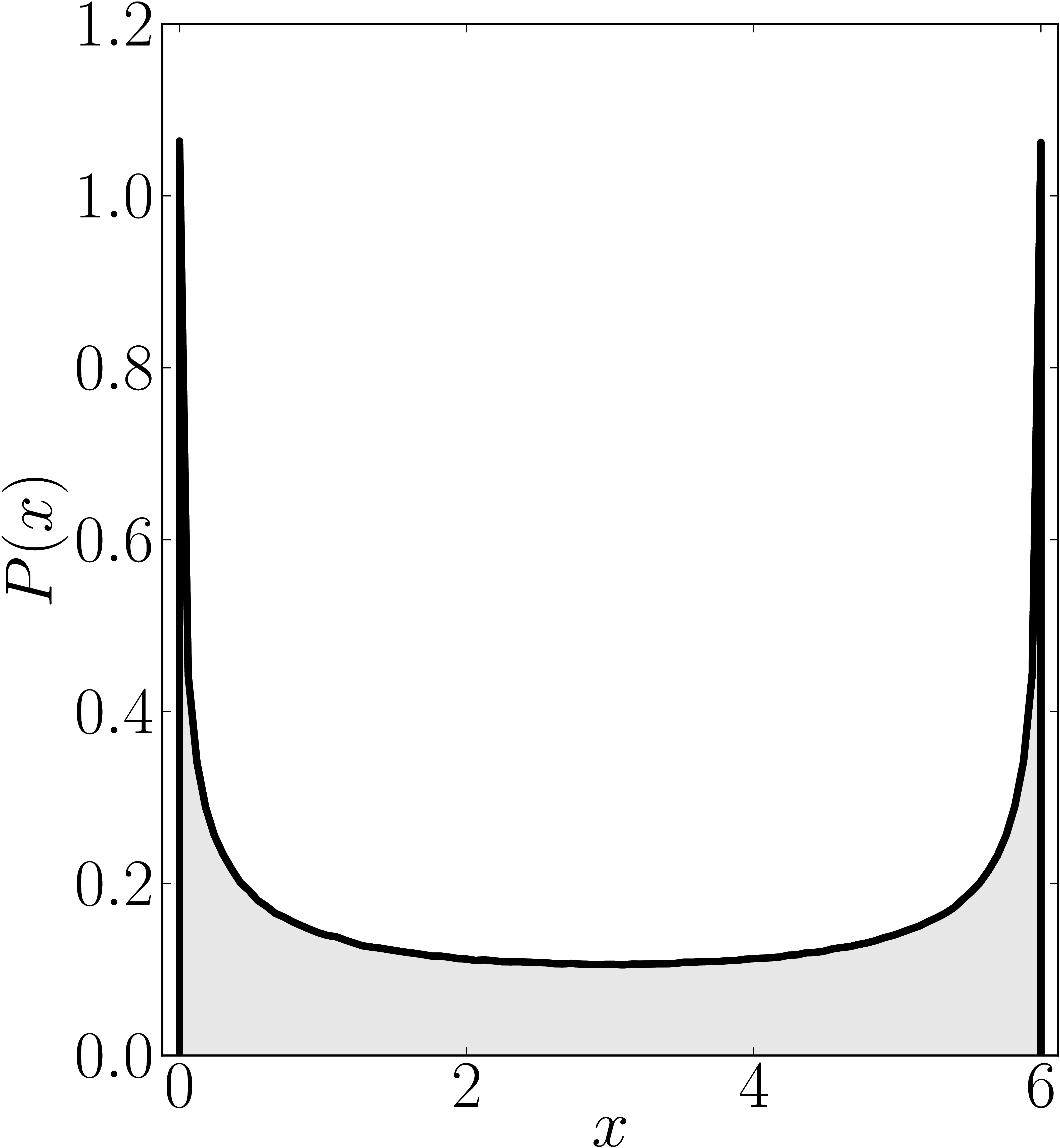
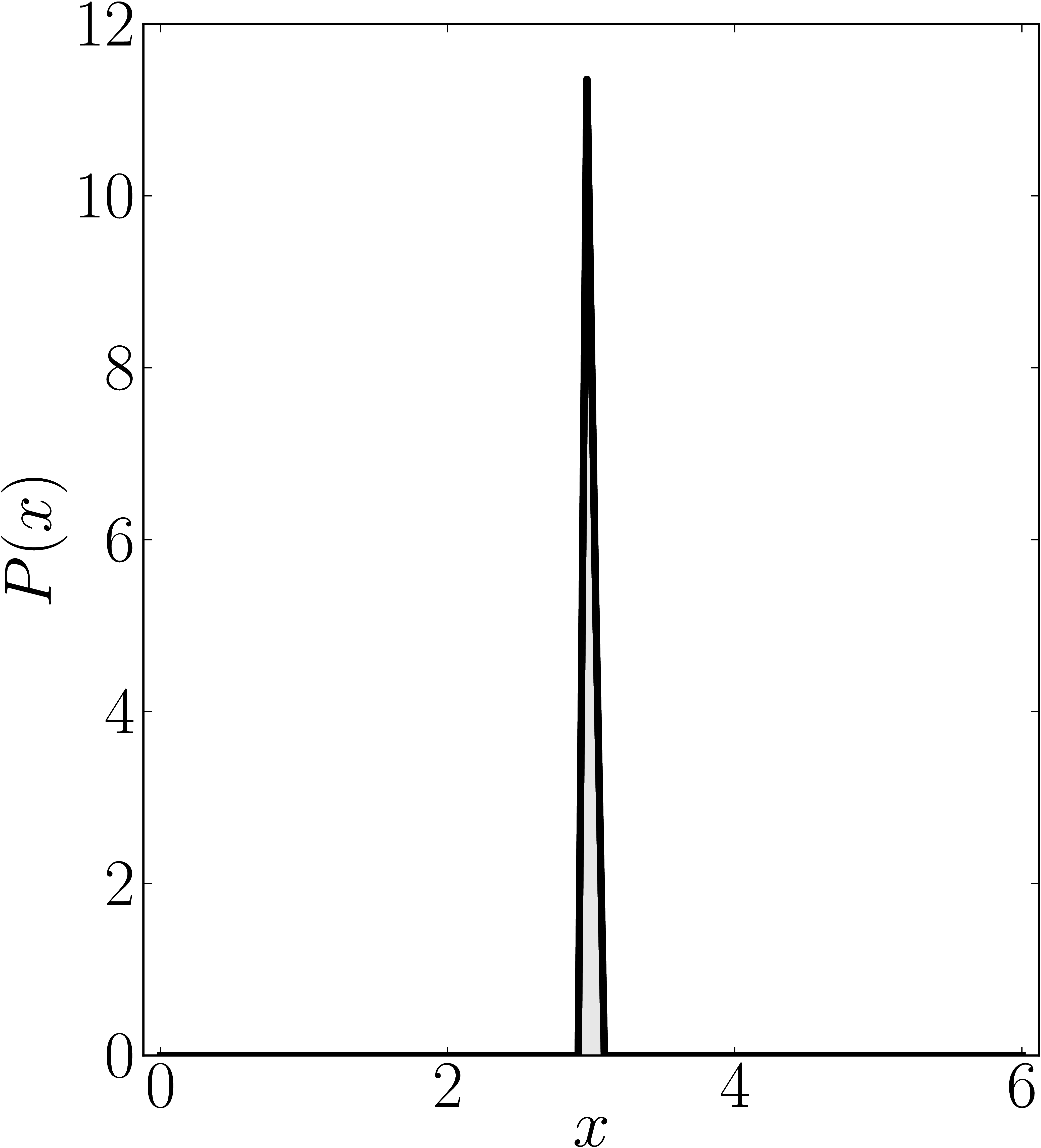
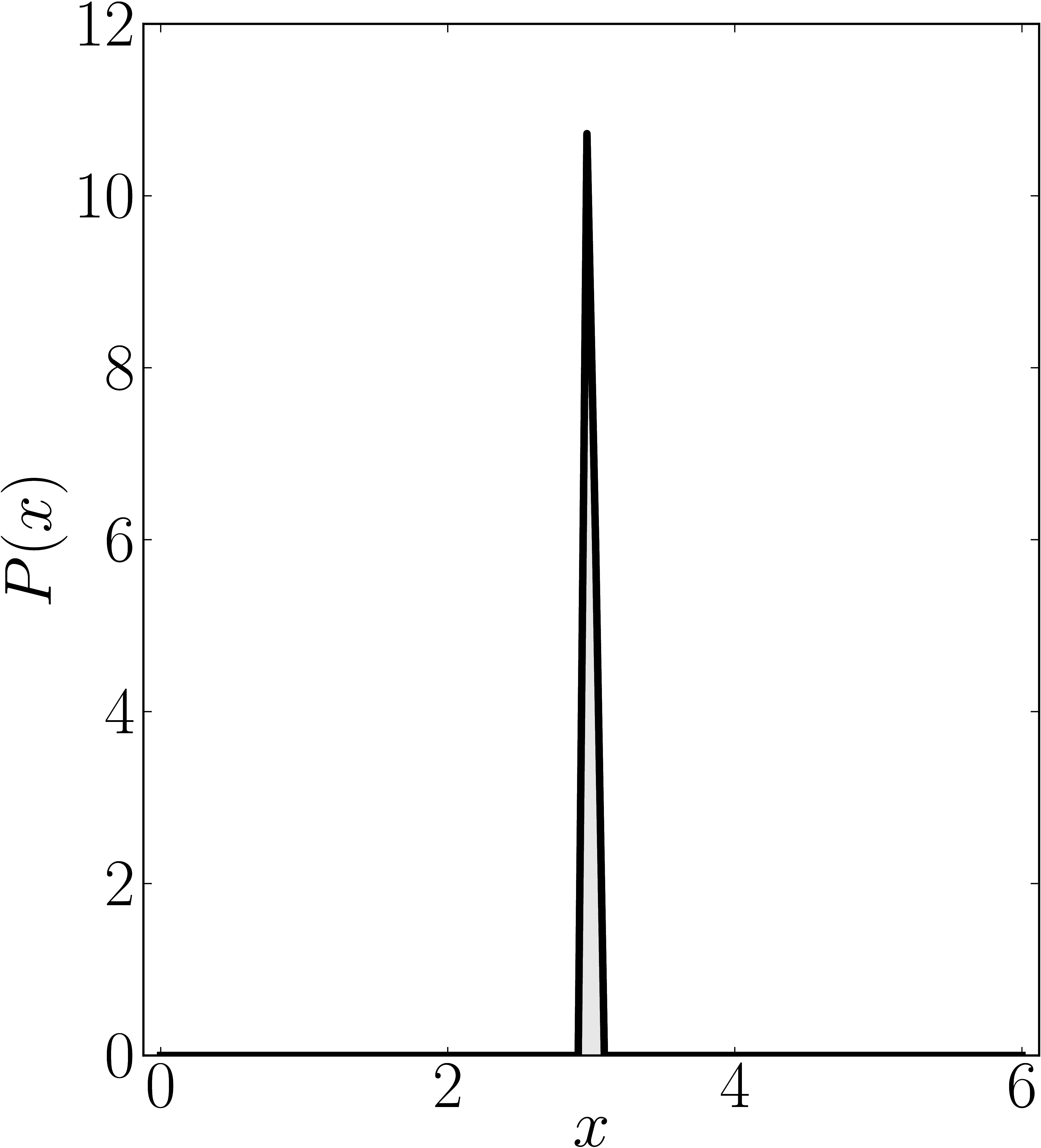
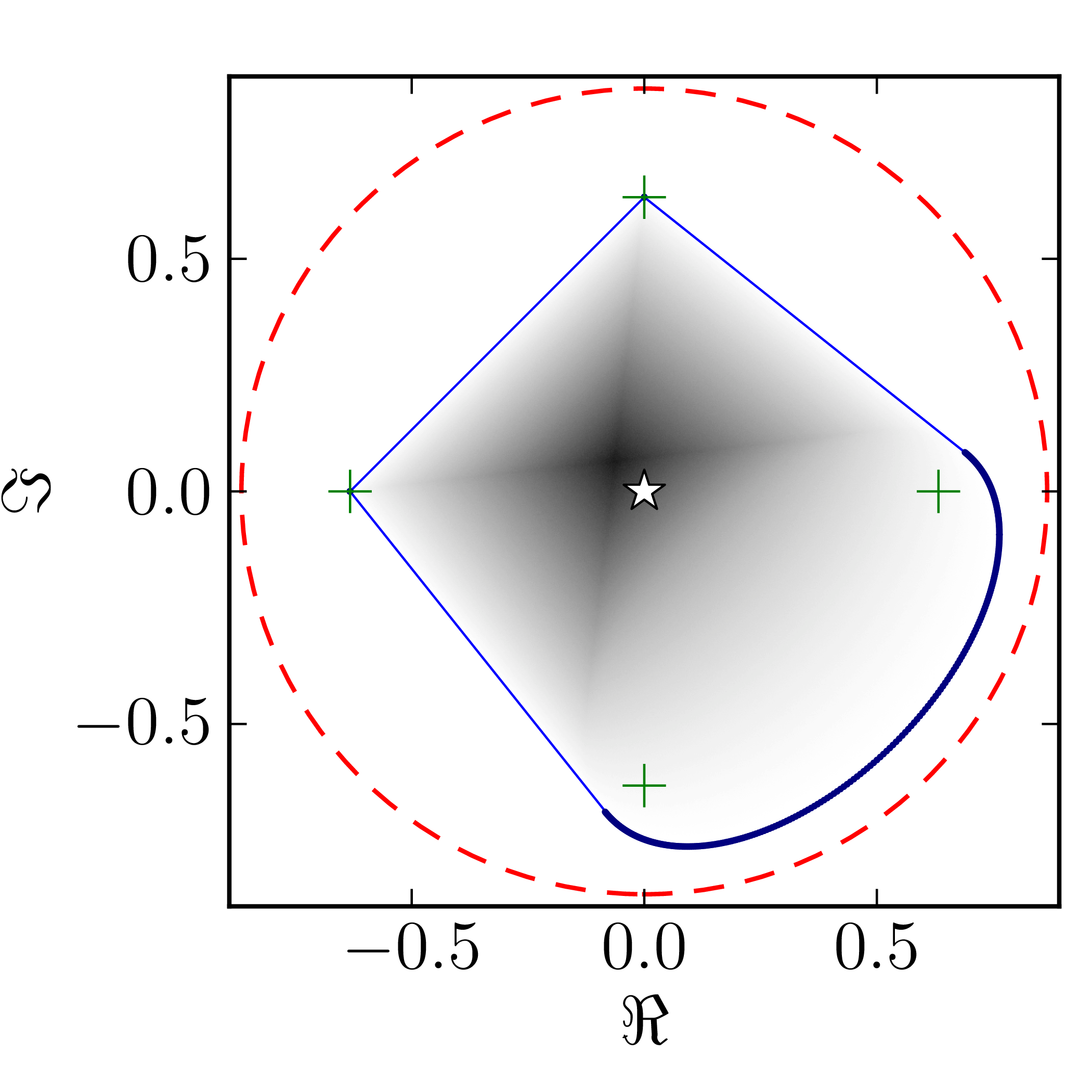
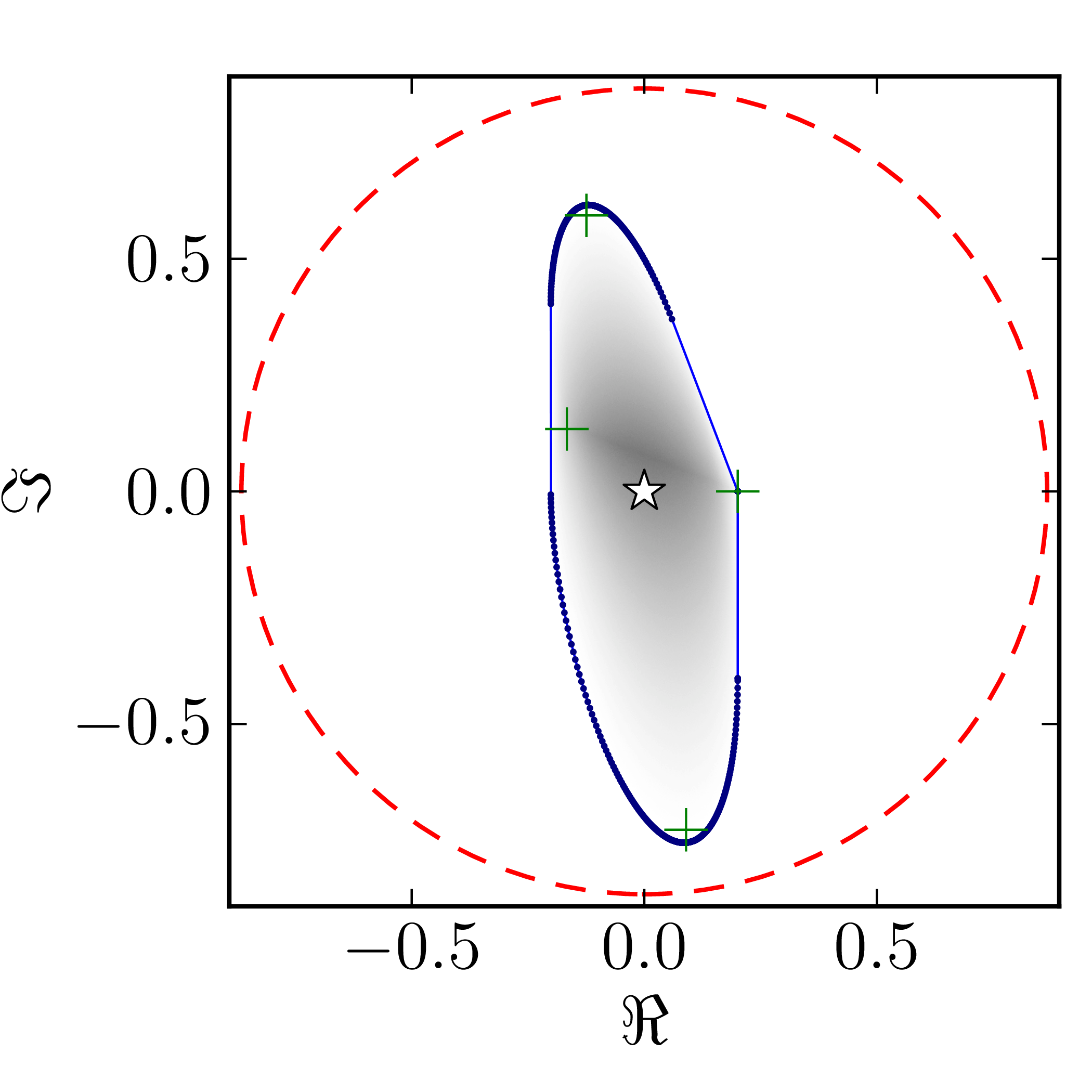
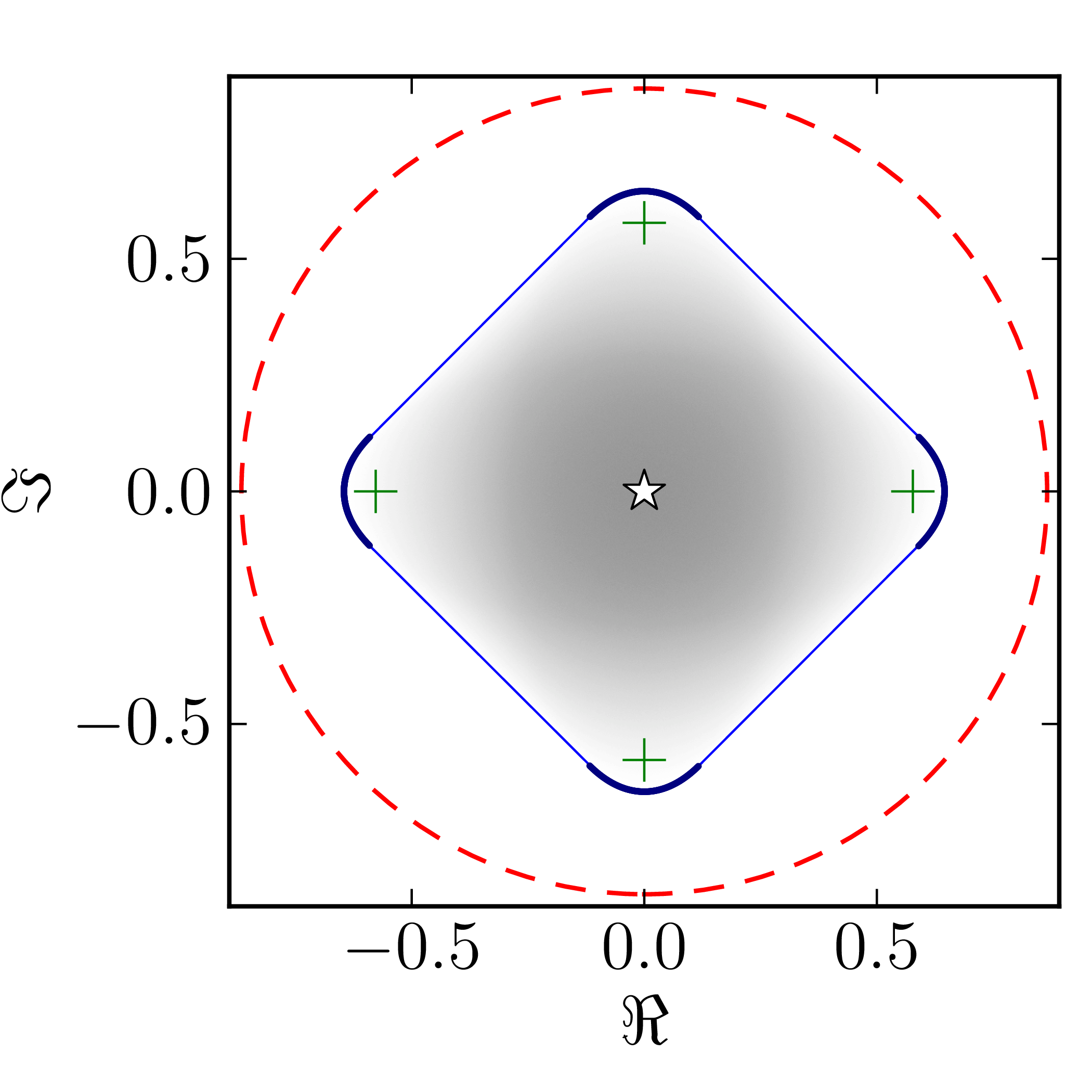
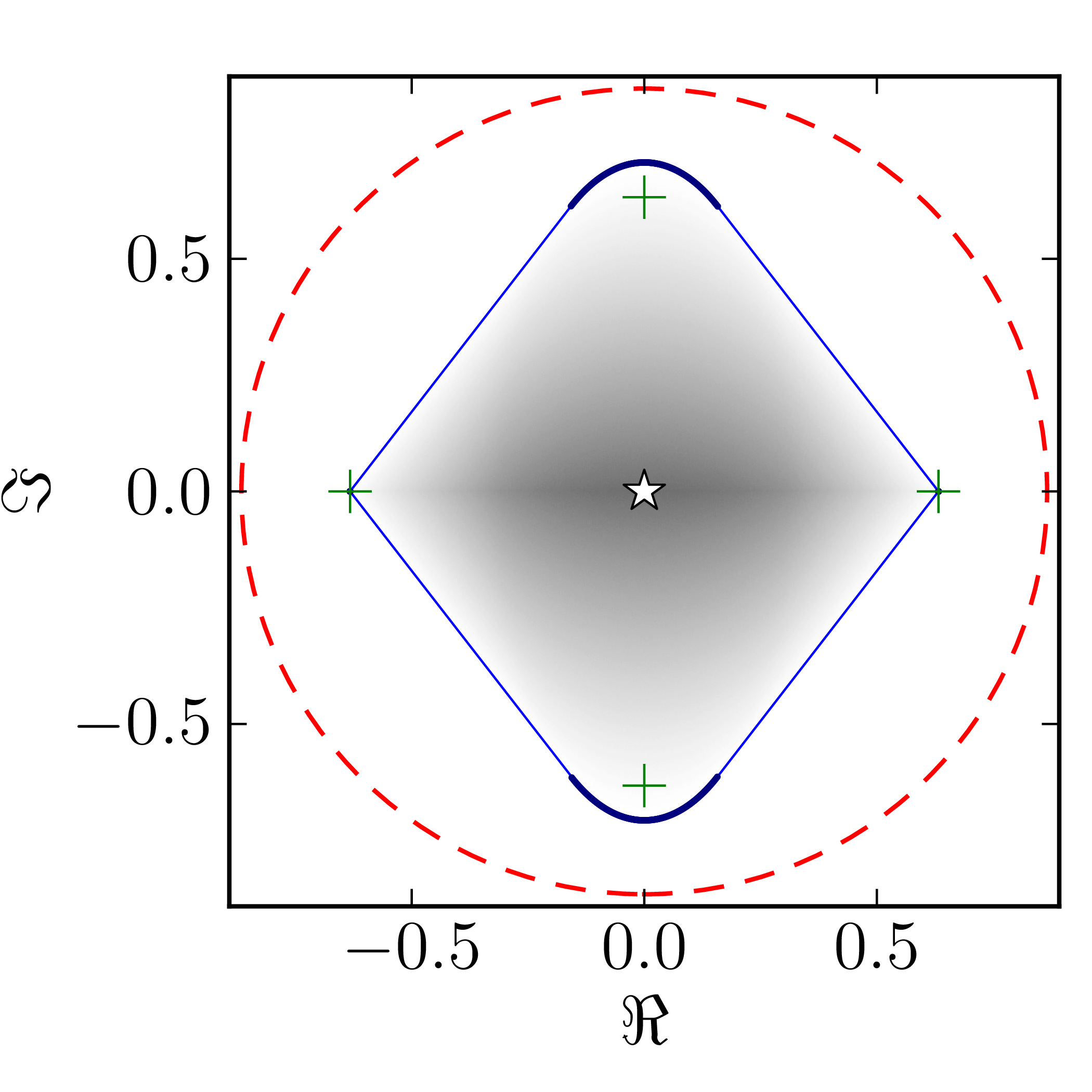
In the case of Hermitian matrices the numerical shadow is a one dimensional distribution.
The matrix is $\mathrm{diag}(0,0,4,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,1,4,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,2,4,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,3,4,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,4,4,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,4,5,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,4,6,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,6,6,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is $\mathrm{diag}(0,0,6,6)$
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex product states Numerical shadow with respect to real product states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
The matrix is TODO:fill. We present the (restricted) numerical shadow for the following cases:
1 all pure states (standard shadow), separately for complex and real states 2 product states (product shadow), $|_{} = U_A U_B $ 3 entangled states, $ = U_A U_B( + )/$, separately for complex and real states.
Here $U_A$, $U_B$ are independent random unitary matrices taken from $U(2)$ with respect to the Haar measure.
Standard numerical shadow with respect to complex states Numerical shadow with respect to real states
Numerical shadow with respect to complex separable states Numerical shadow with respect to real separable states
Numerical shadow with respect to complex entangled states Numerical shadow with respect to real entangled states
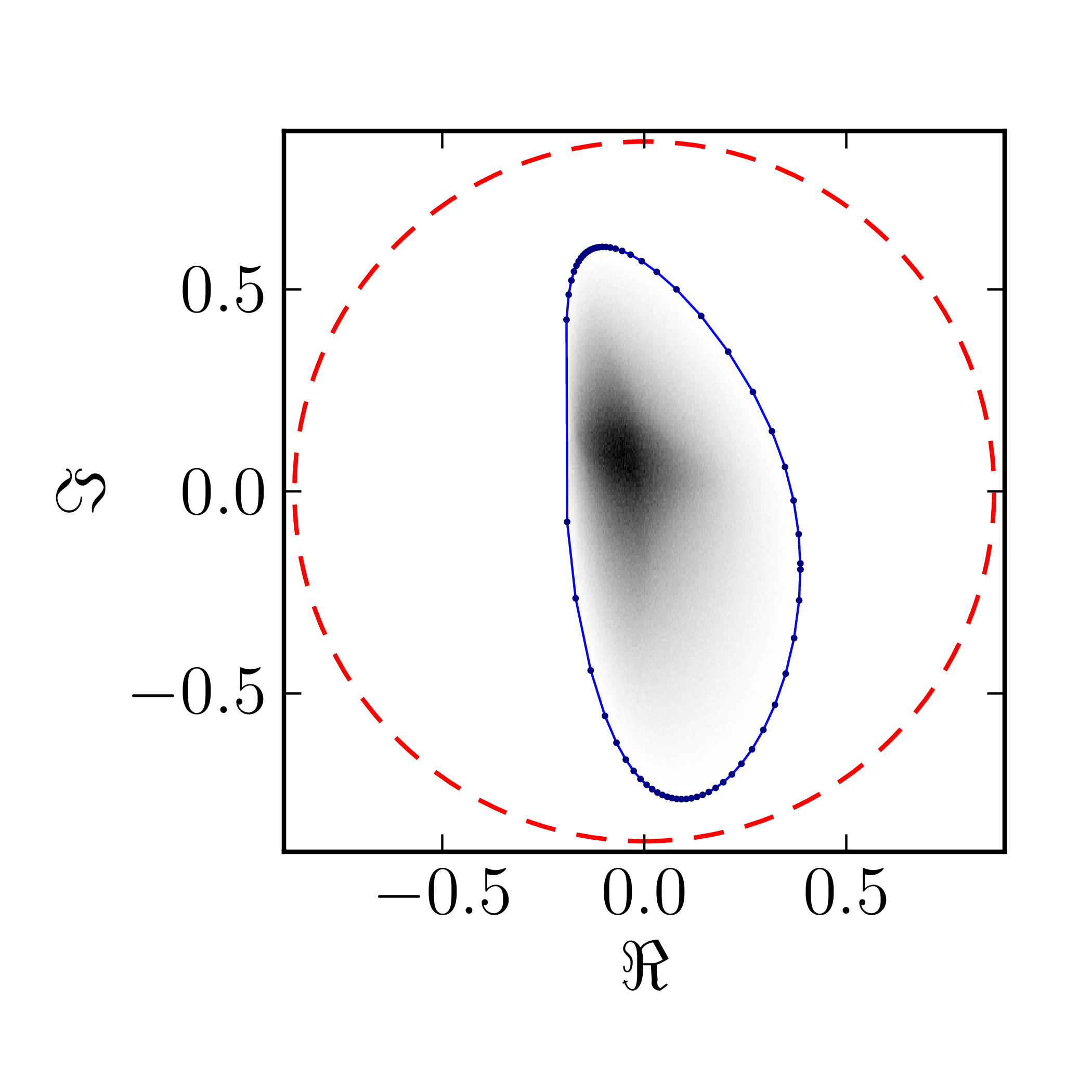
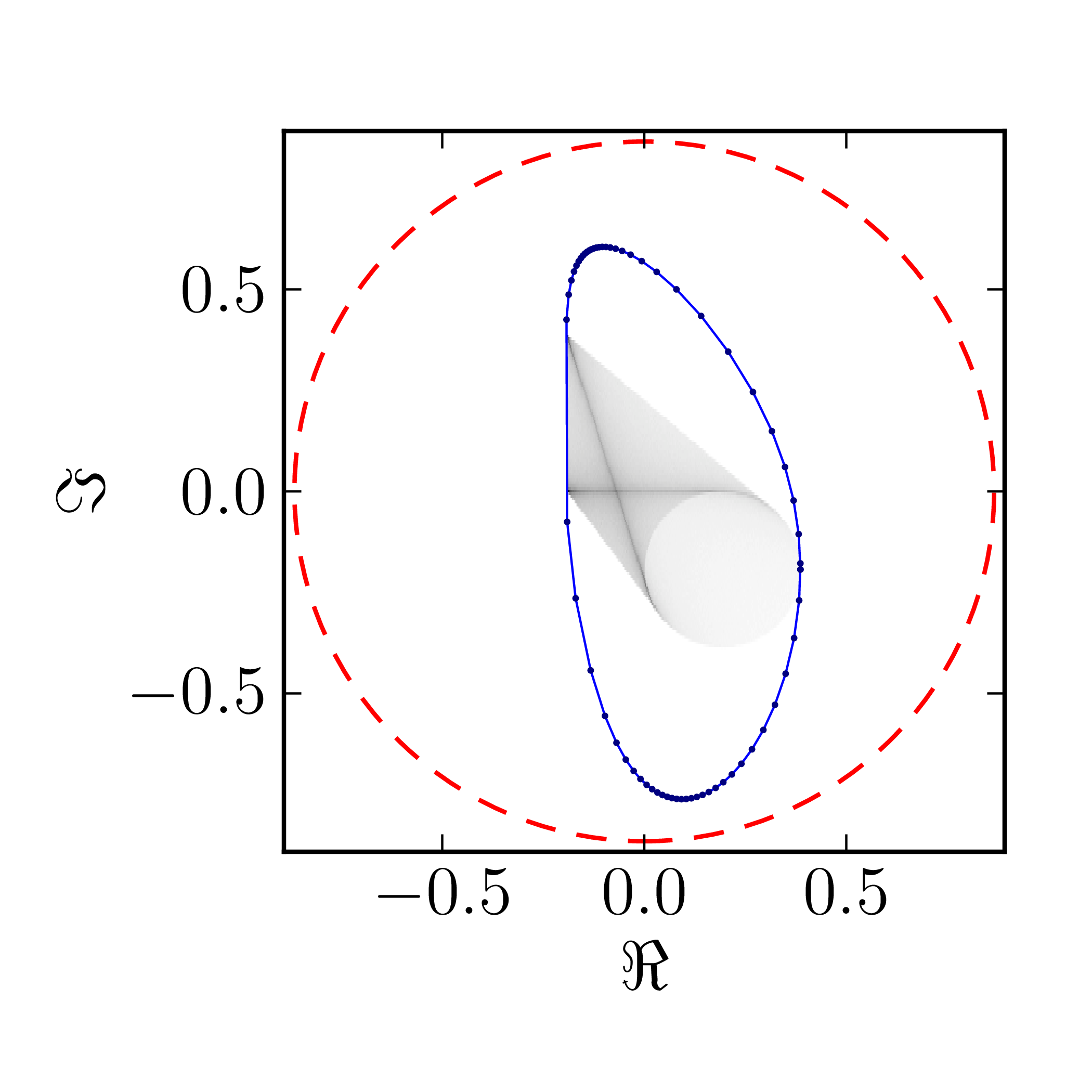
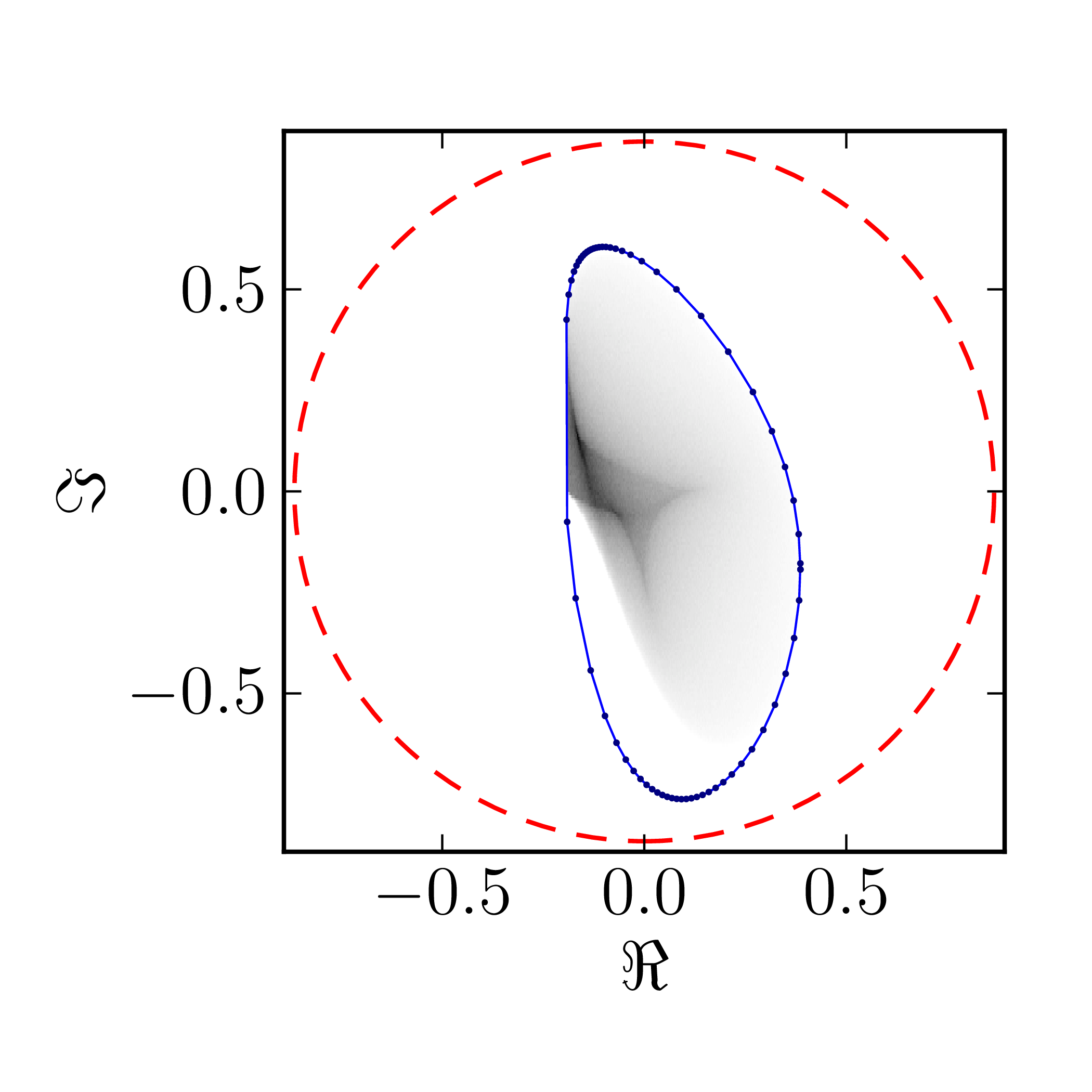
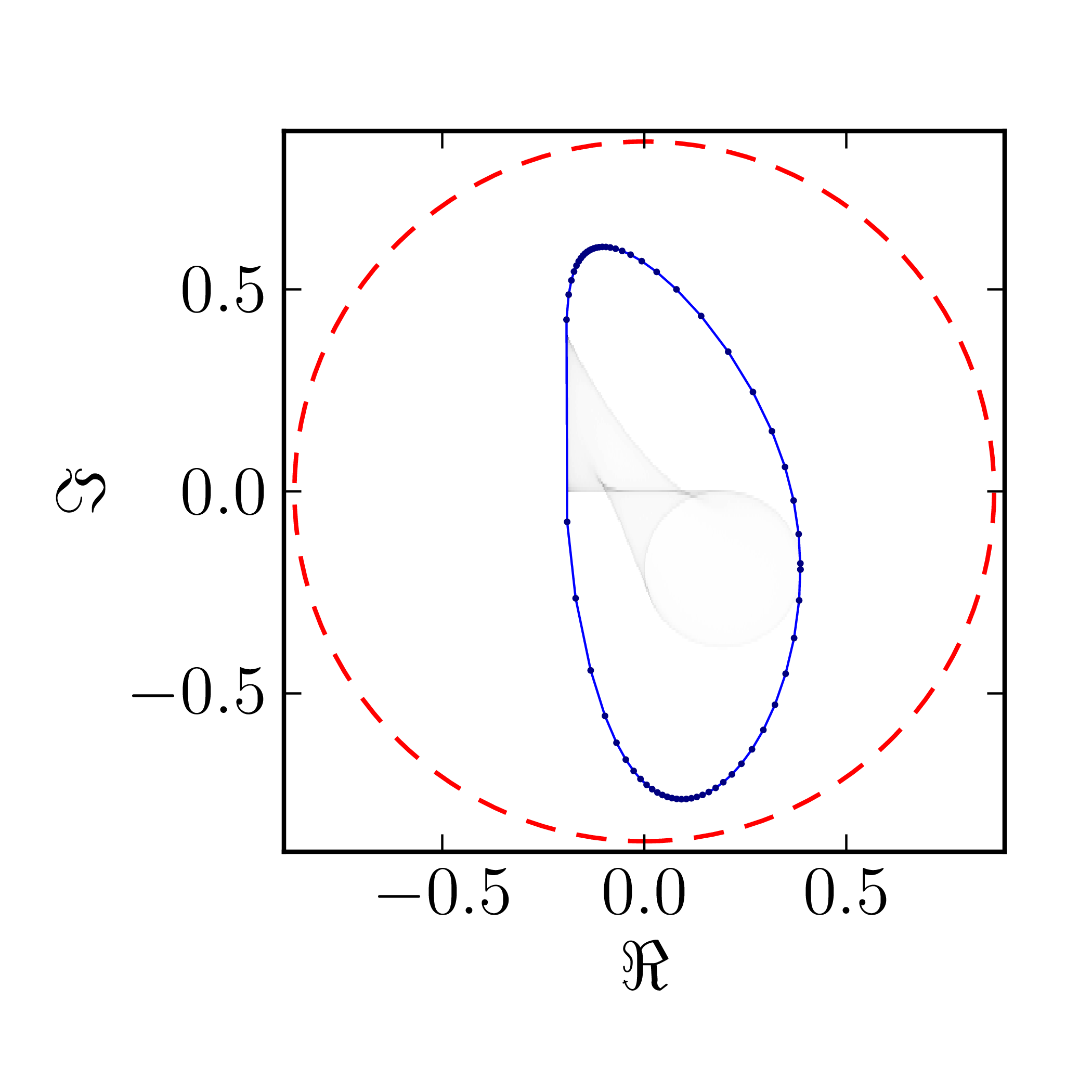
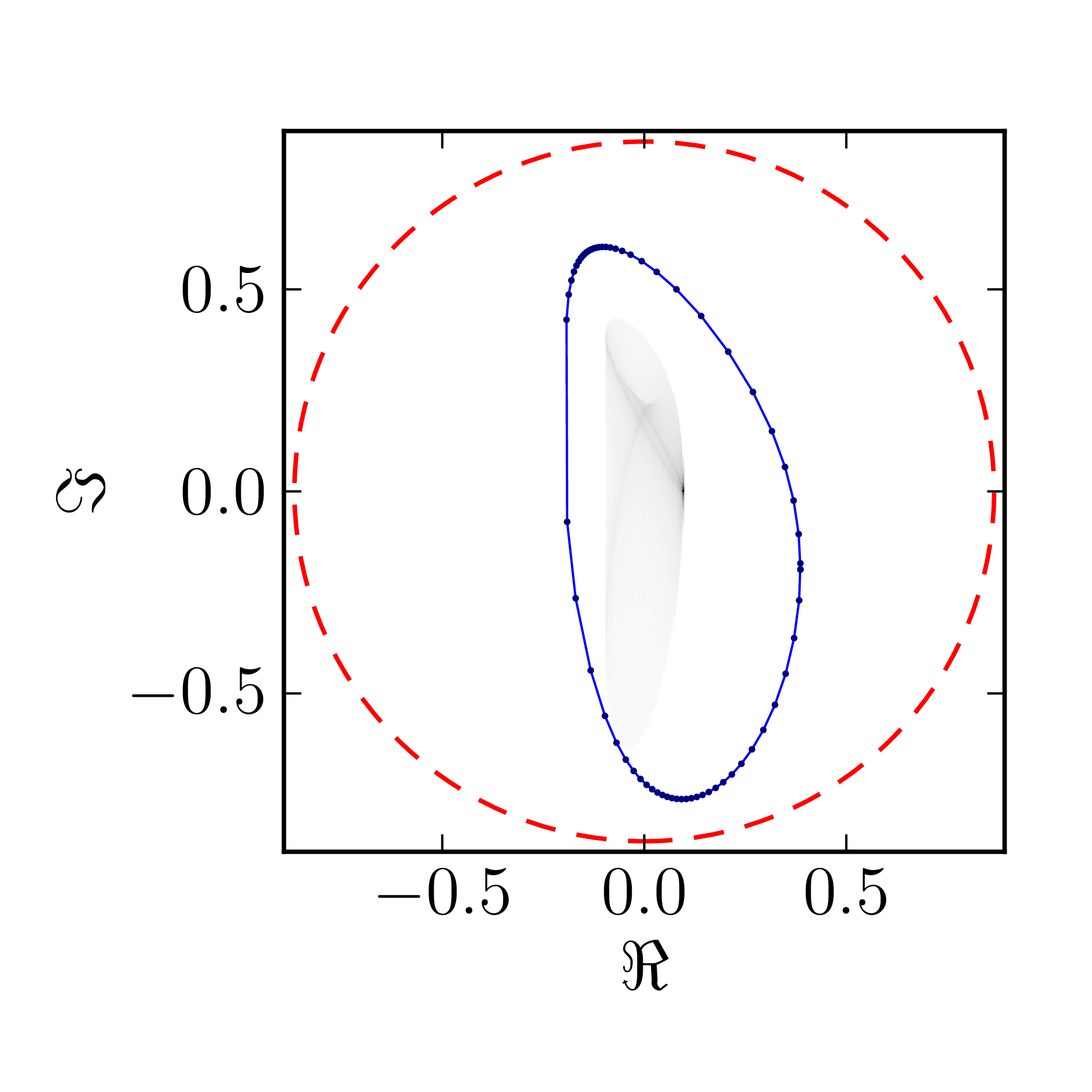
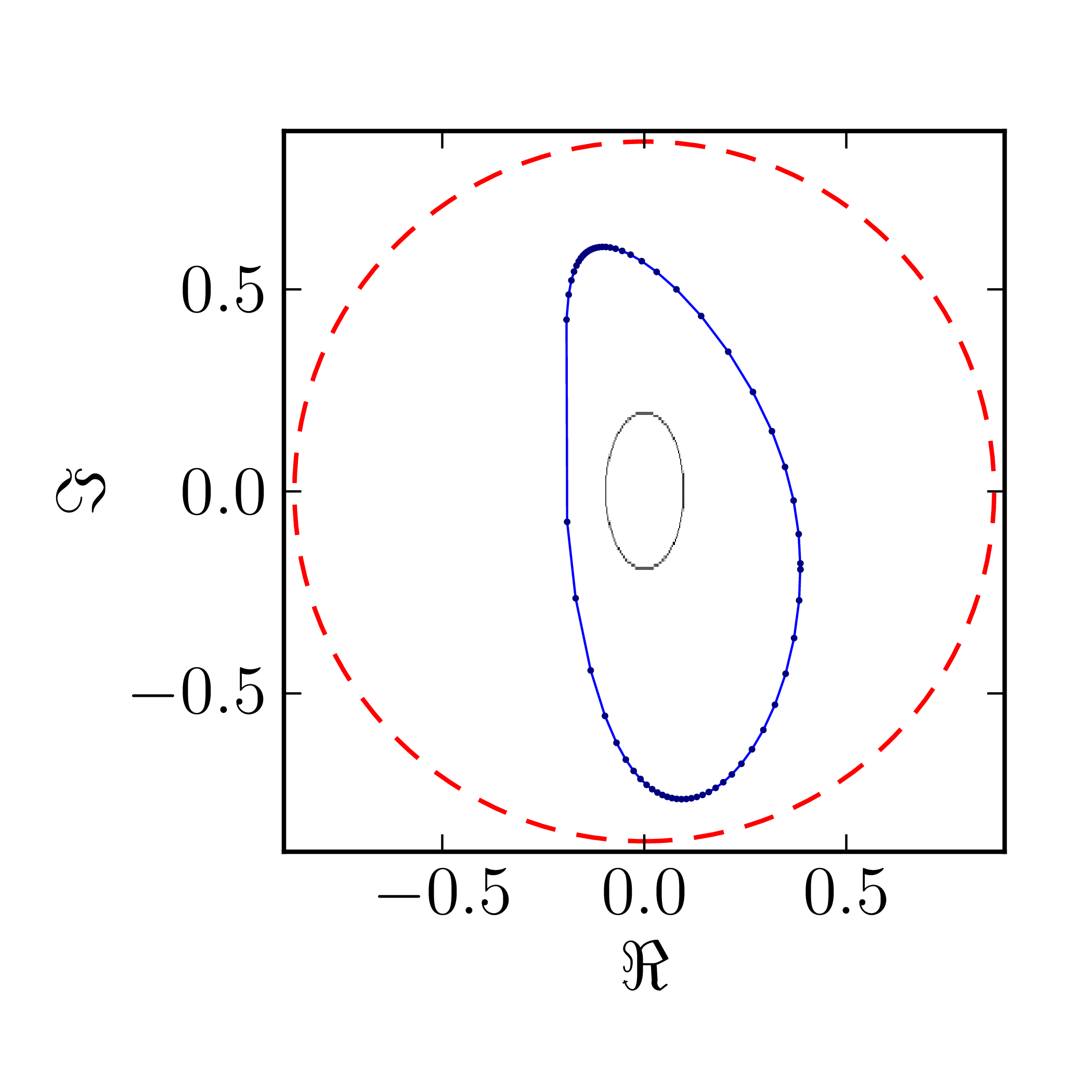
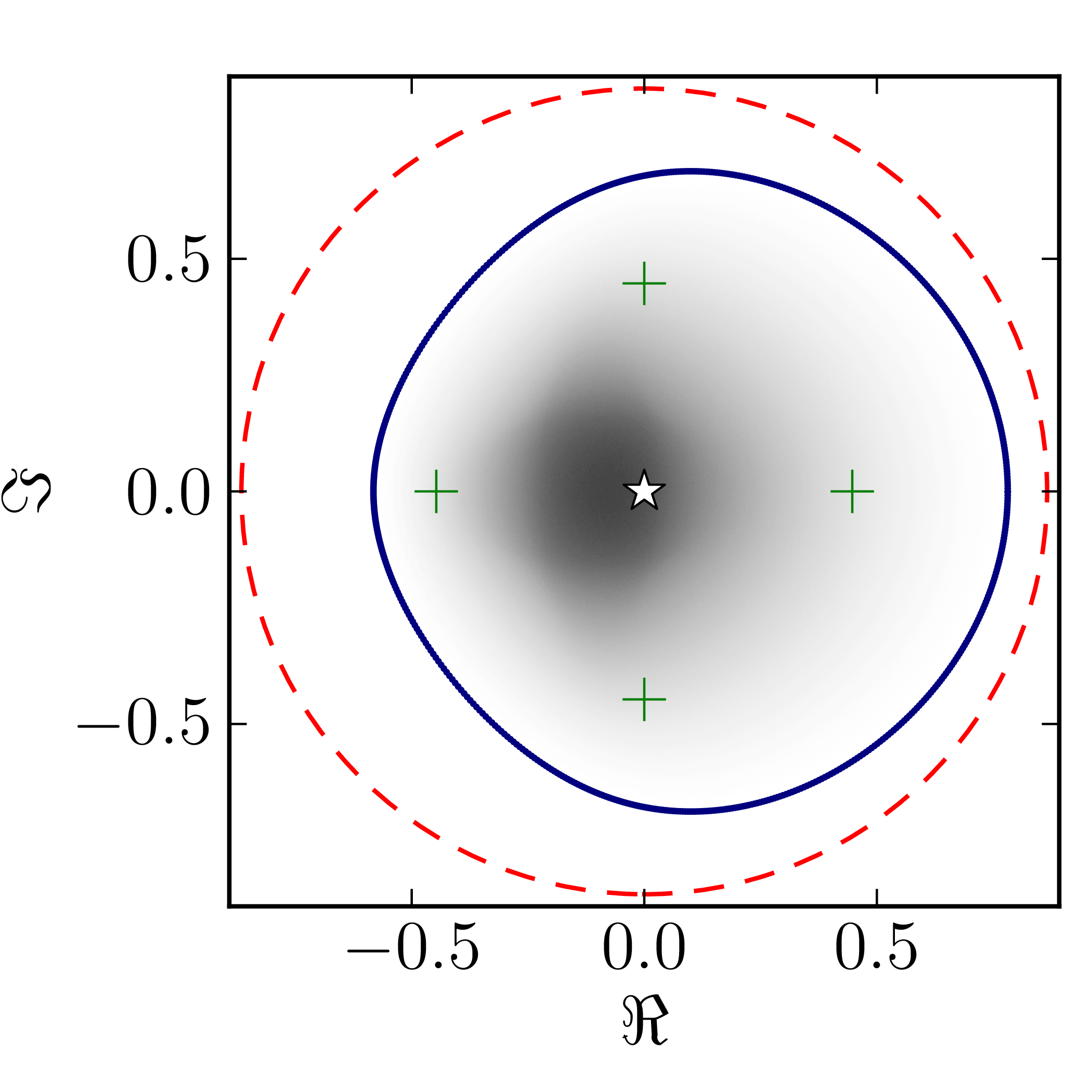
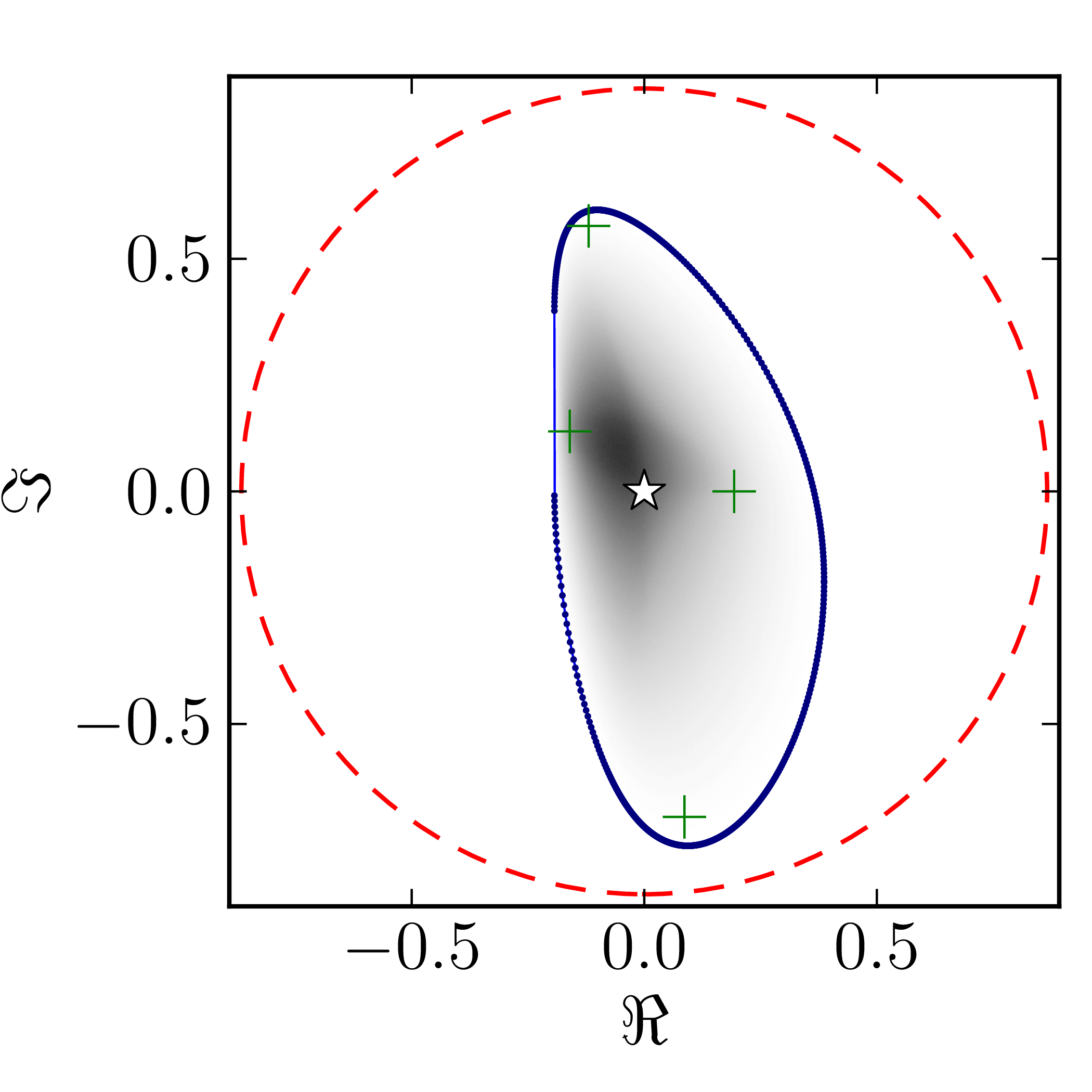
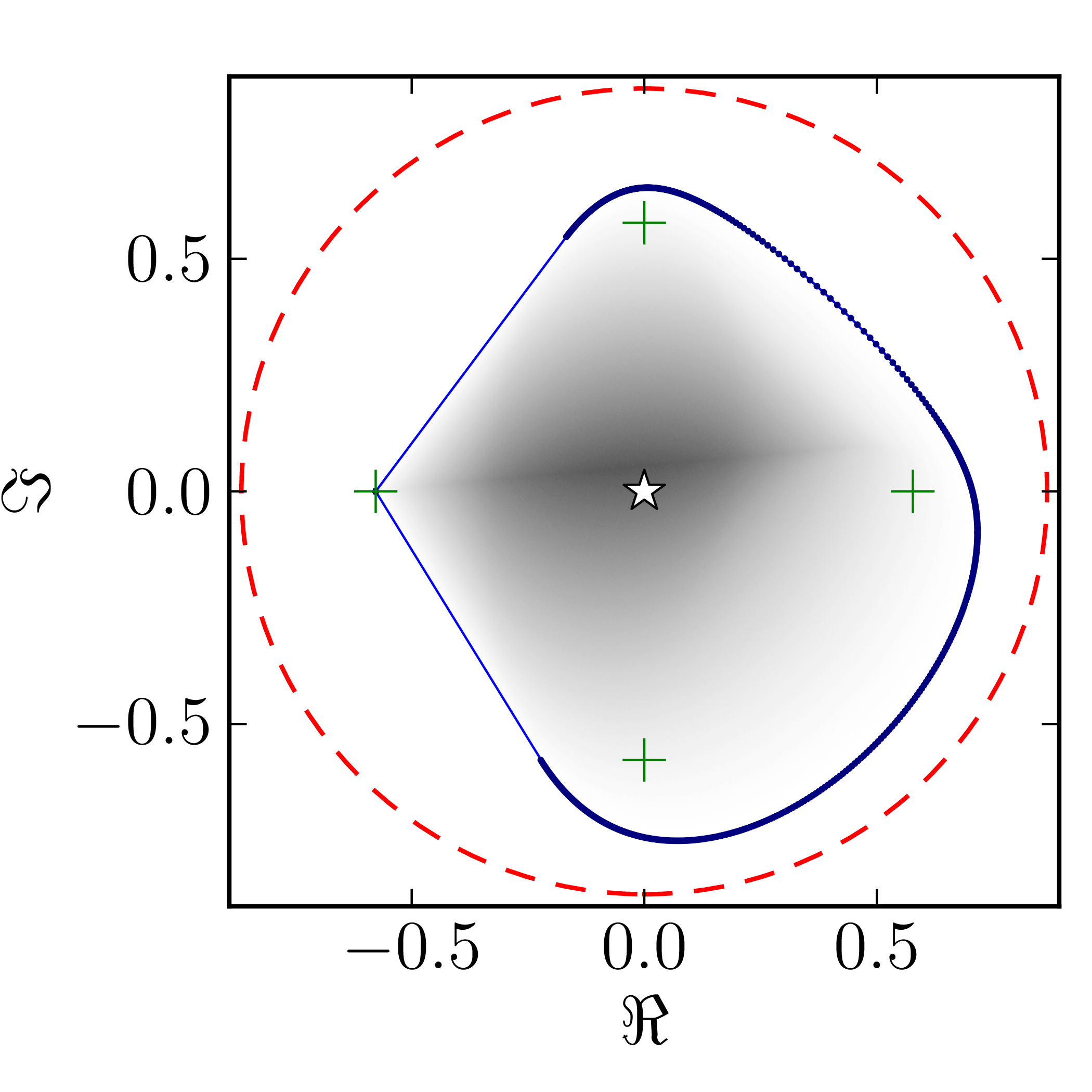
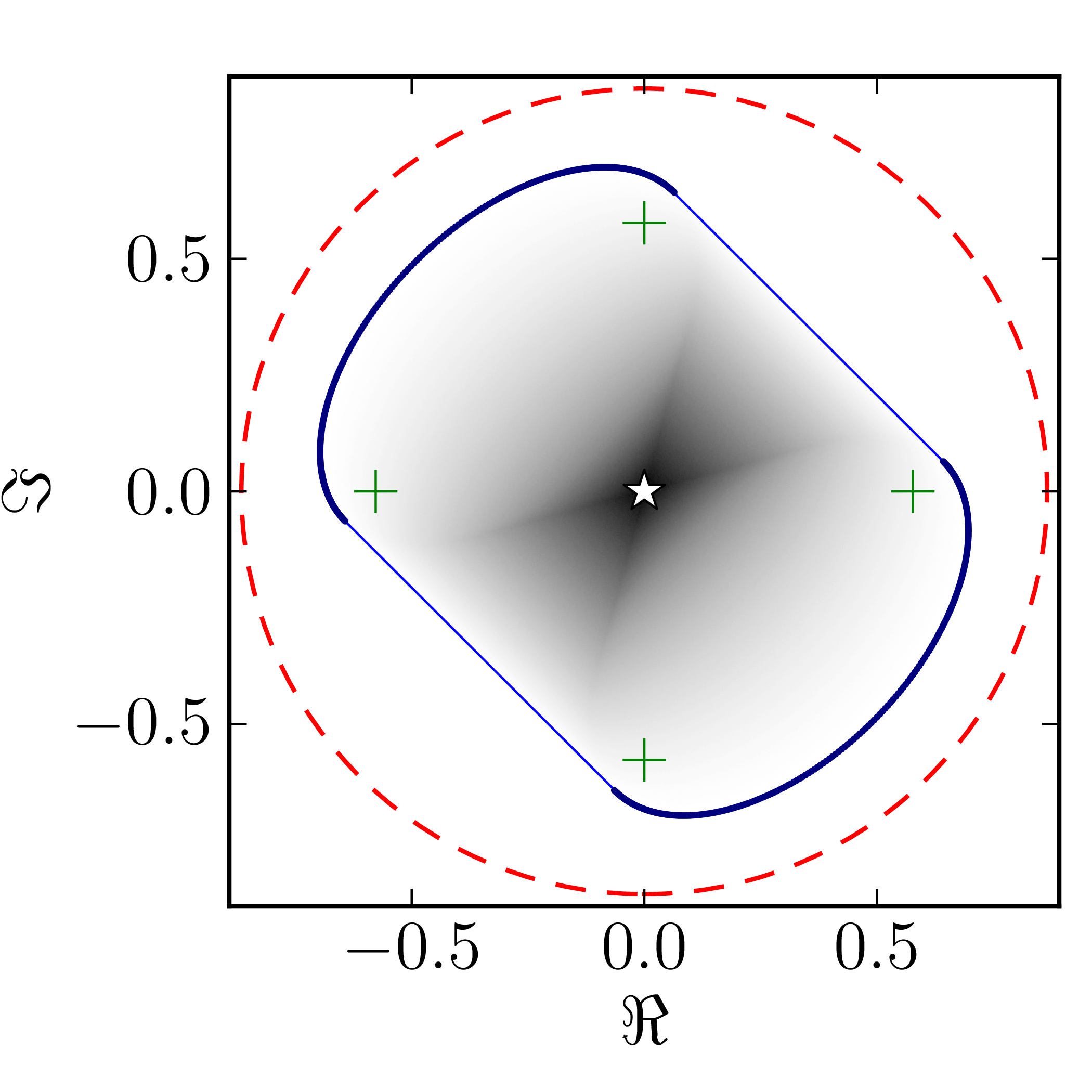
Even though several results on geometry of numerical range for $N = 4$ are available CITATION, complete classification of numerical ranges in this case is still missing. To provide an overview of the possible structure of the numerical shadow we show the complex numerical shadows of the following matrices of order four,
\[ A^{(4)}_0= \begin{pmatrix} 1 & 1 & 1 & 1 \\ 0 & \mathrm{i} & 1 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_1= \begin{pmatrix} \mathrm{i} & 0 & -1 & 0 \\ 0 & 0 & -1 & 0 \\ 1 & 1 & 1-\mathrm{i} & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix}, \] \[ A^{(4)}_2= \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & \mathrm{i} & 0 & 1 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_3= \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & \mathrm{i} & 1 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_4= \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & \mathrm{i} & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_5= \begin{pmatrix} \mathrm{i} & 0 & -1 & 0 \\ 0 & 0 & -1 & 0 \\ 1 & 1 & 1-\mathrm{i} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}, \] \[ A^{(4)}_6= \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & \mathrm{i} & 0 & 1 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_7= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \mathrm{i} & 0 & 1 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}, \] \[ A^{(4)}_8= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \mathrm{i} & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -\mathrm{i} \end{pmatrix}. \]
$A_0^{(4)}$ $A_1^{(4)}$
$A_2^{(4)}$ $A_3^{(4)}$
$A_4^{(4)}$ $A_5^{(4)}$
$A_6^{(4)}$ $A_7^{(4)}$
$A_8^{(4)}$