Product numerical range
Definition
Product numerical range $W^\otimes(A)$ of a square matrix $A$ of size $d = d_1 d_2$ is a subset of the complex plane defined as
\[\begin{split} W^\otimes(A)=\left\{z \in \mathbb{C}:\ z= \left( \bra{\psi} \otimes \bra{\phi} \right) A \left( \ket{\psi} \otimes \ket{\phi} \right), \ket{\psi}\in\mathbb{C}^{d_1}, \ket{\phi}\in\mathbb{C}^{d_2}\\ \braket{\psi}{\psi}=1, \braket{\phi}{\phi}=1 \right\}. \end{split}\]In general, this definition can be written as: product numerical range $W^\otimes(A)$ of a square matrix $A$ of dimension $d = \prod_{i=1}^K d_i$ is a subset of the complex plane defined as
\[\begin{split} W^\otimes(A)=\left\{z \in \mathbb{C}:\ z= \left( \bigotimes_{i=1}^K \bra{\psi_i} \right) A \left( \bigotimes_{i=1}^K \ket{\psi_i} \right), \ket{\psi_i}\in\mathbb{C}^{d_i}, \\ \braket{\psi_i}{\psi_i}=1 \text{ for }\ i=1,\ldots,K \right\}. \end{split}\]Examples
Example 1
Consider a family of operators with a tensor product structure
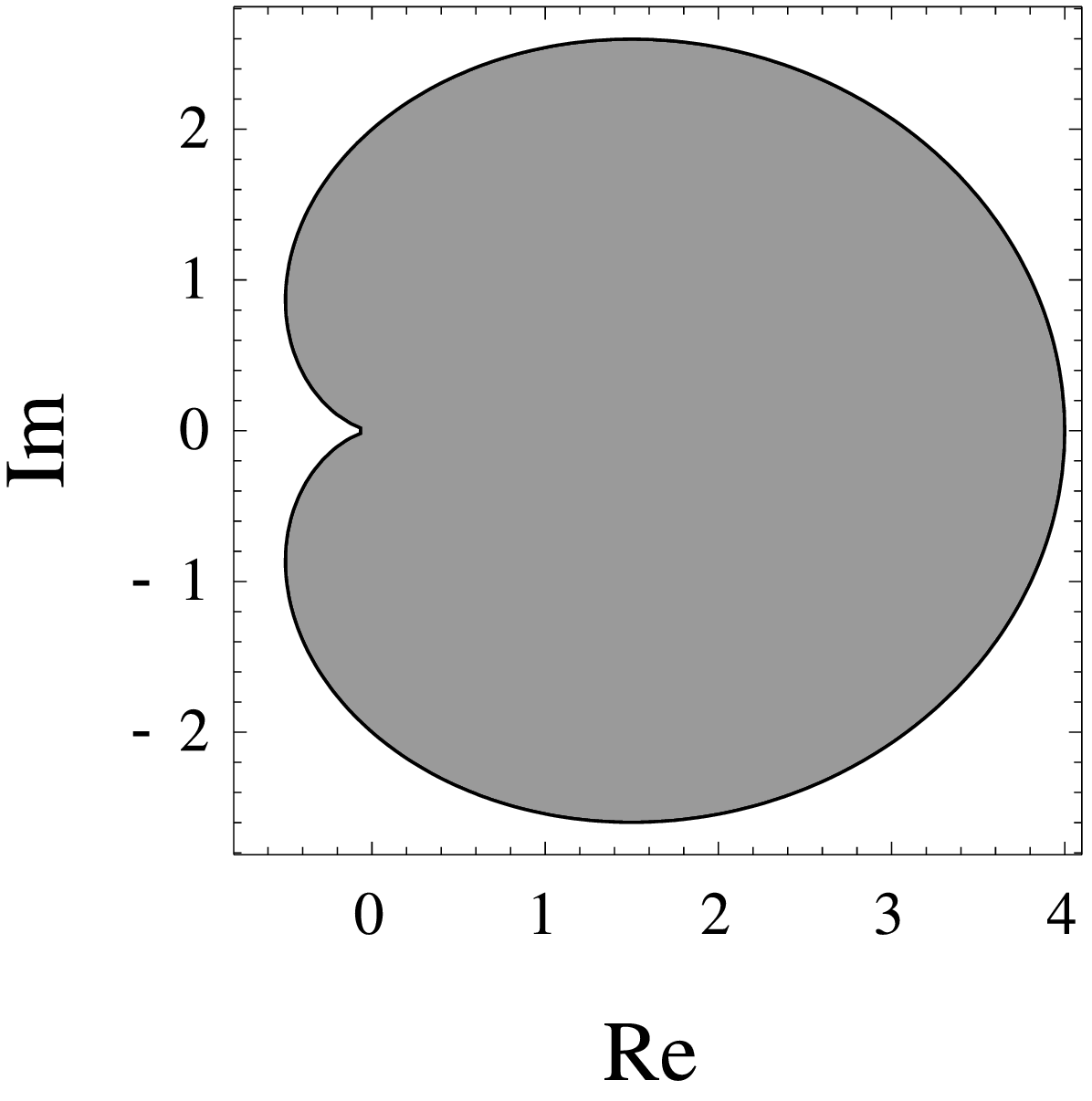
\[Y(r_1,r_2) = X_1 \otimes X_2 = \begin{pmatrix} 1 & 2 r_1 \\ 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} 1 & 2r_2 \\ 0 & 1 \end{pmatrix} .\]Example numerical ranges dependent on $r_1$ and $r_2$ are shown below.
| $(r_1, r_2)$ equal to $(1,1)$ (cardioid) |
|---|
 |
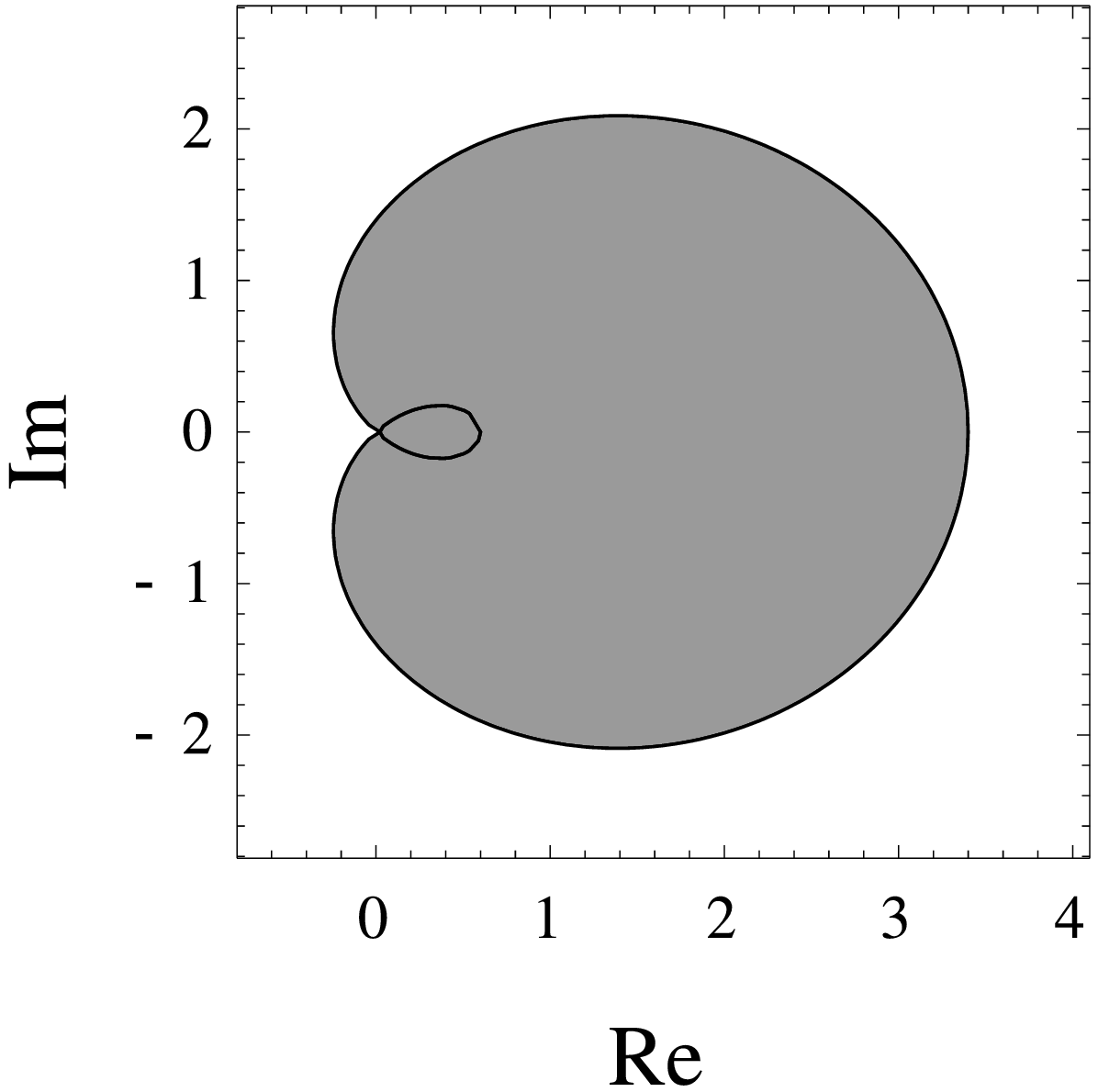
| $(r_1, r_2)$ equal to $(0.7,1)$ (limacon of Pascal) |
|---|
 |
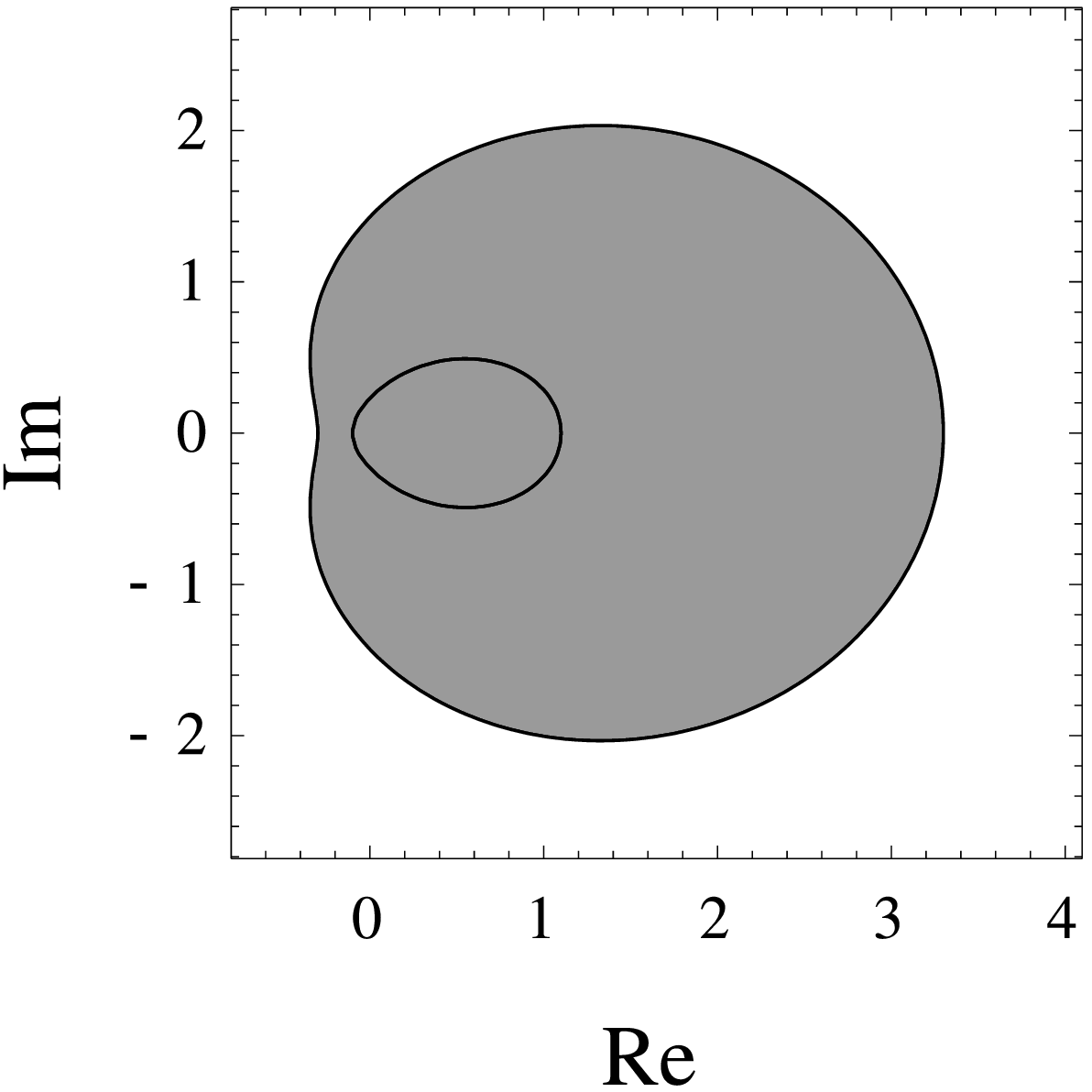
| $(r_1, r_2)$ equal to $(0.5,1.2)$ (Cartesian oval) |
|---|
 |
Example 2
| $(r_1, r_2)$ equal to $(0.5,1.2)$ (Cartesian oval) |
|---|
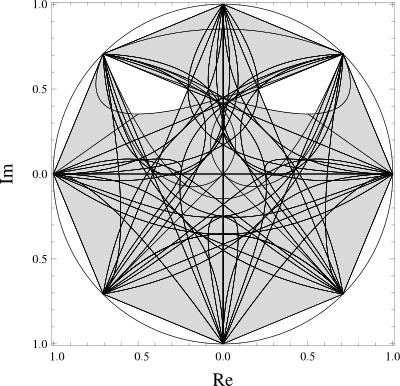 |
Figure: Product numerical range [1] with respect to four-qubit space given by the equation \(W^\otimes(A)=\{z:\ z= \left( \bigotimes_{i=1}^4 \langle\psi_i| \right) A \left( \bigotimes_{i=1}^4 |\psi_i\rangle \right), \text{ for } i=1,\ldots,4\ \langle\psi_i|\psi_i\rangle=1 \text{ and } |\psi_i\rangle\in\mathbb{C}^2 \}\) of the matrix $ A ={\rm diag} \bigl( e^{\frac{i \pi }{4}},i,i,e^{\frac{3 i \pi }{4}},-1,e^{-\frac{3 i \pi }{4}}, e^{-\frac{i \pi }{4}},1,-1,e^{-\frac{i \pi }{4}},e^{-\frac{3 i \pi }{4}},1, e^{\frac{3 i \pi }{4}},-i,-i,e^{\frac{i \pi }{4}} \bigr). $
References
- [1]Z. Puchała, P. Gawron, J. A. Miszczak, Ł. Skowronek, M. D. Choi, and K. Życzkowski, “Product numerical range in a space with tensor product structure,” Linear Algebra and its Applications, vol. 434, no. 1, pp. 327–342, 2011, [Online]. Available at: https://www.sciencedirect.com/science/article/pii/S0024379510004349.