8x8 matrices

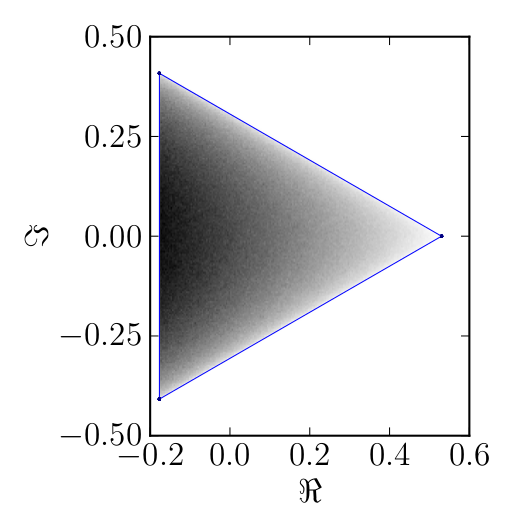
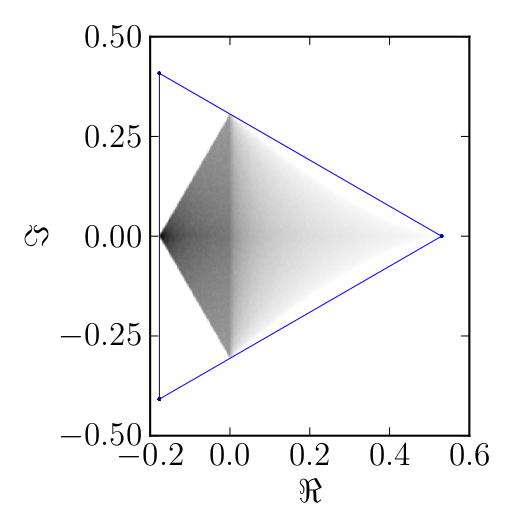
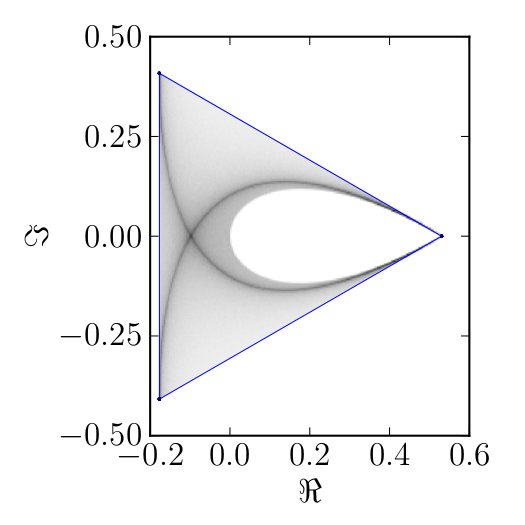
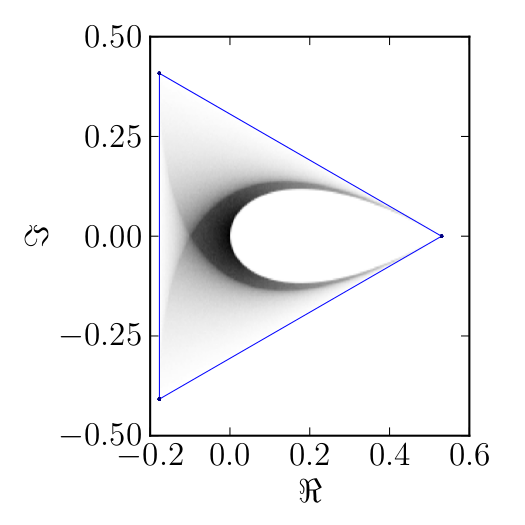
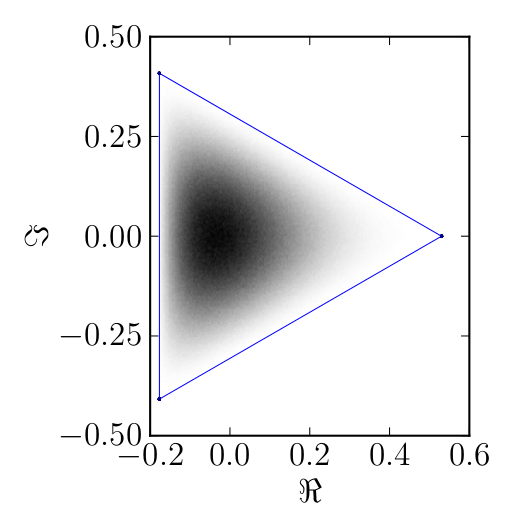
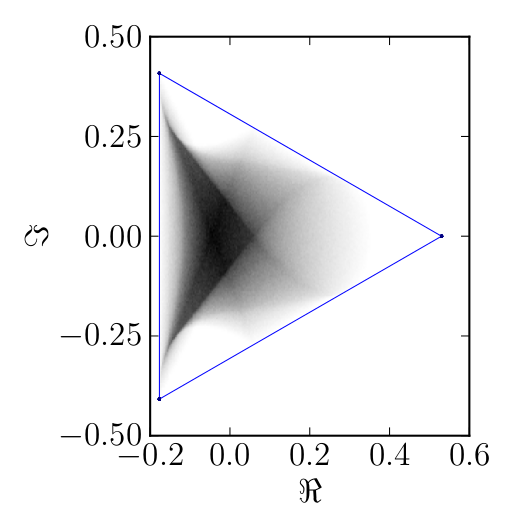
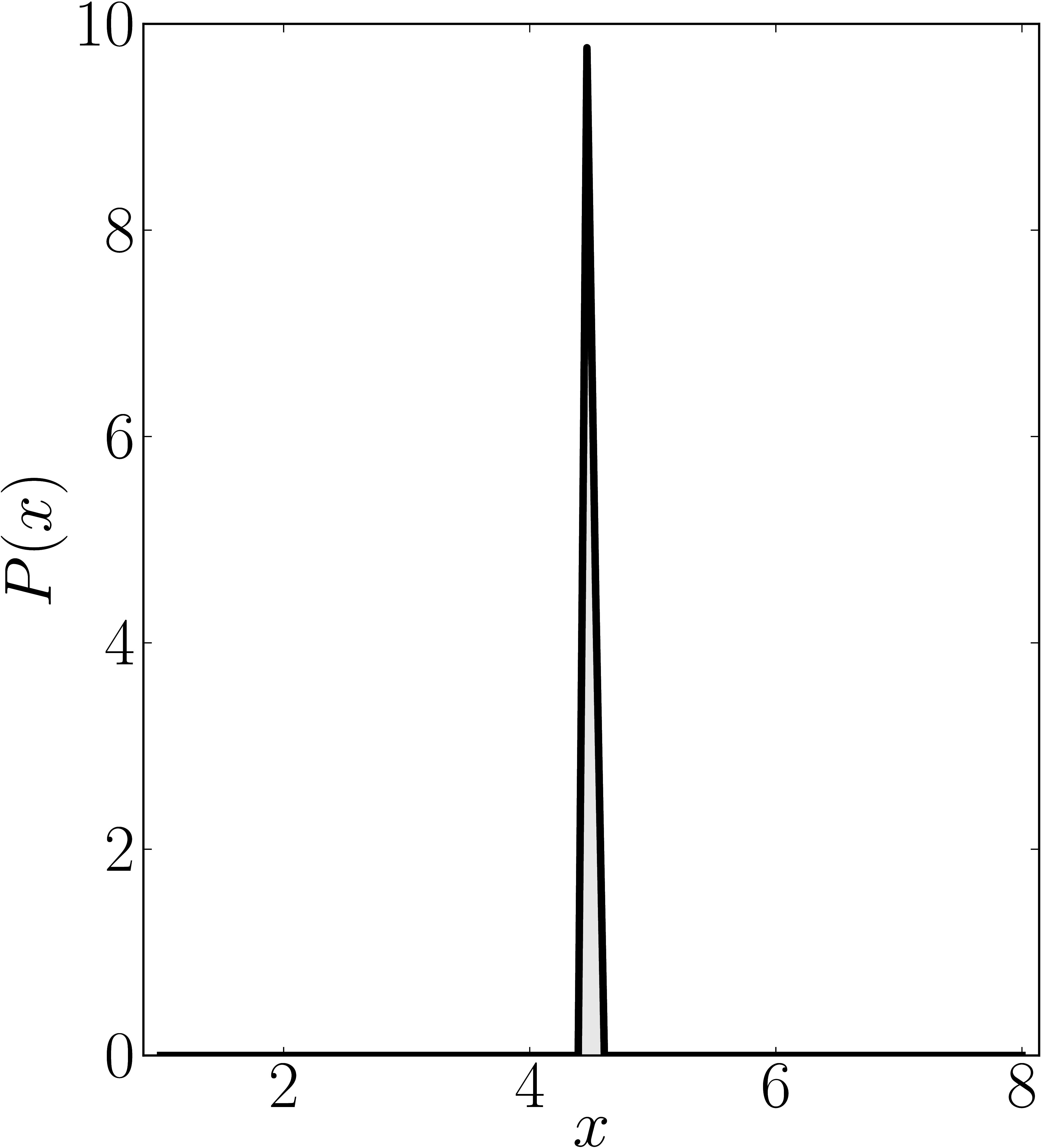
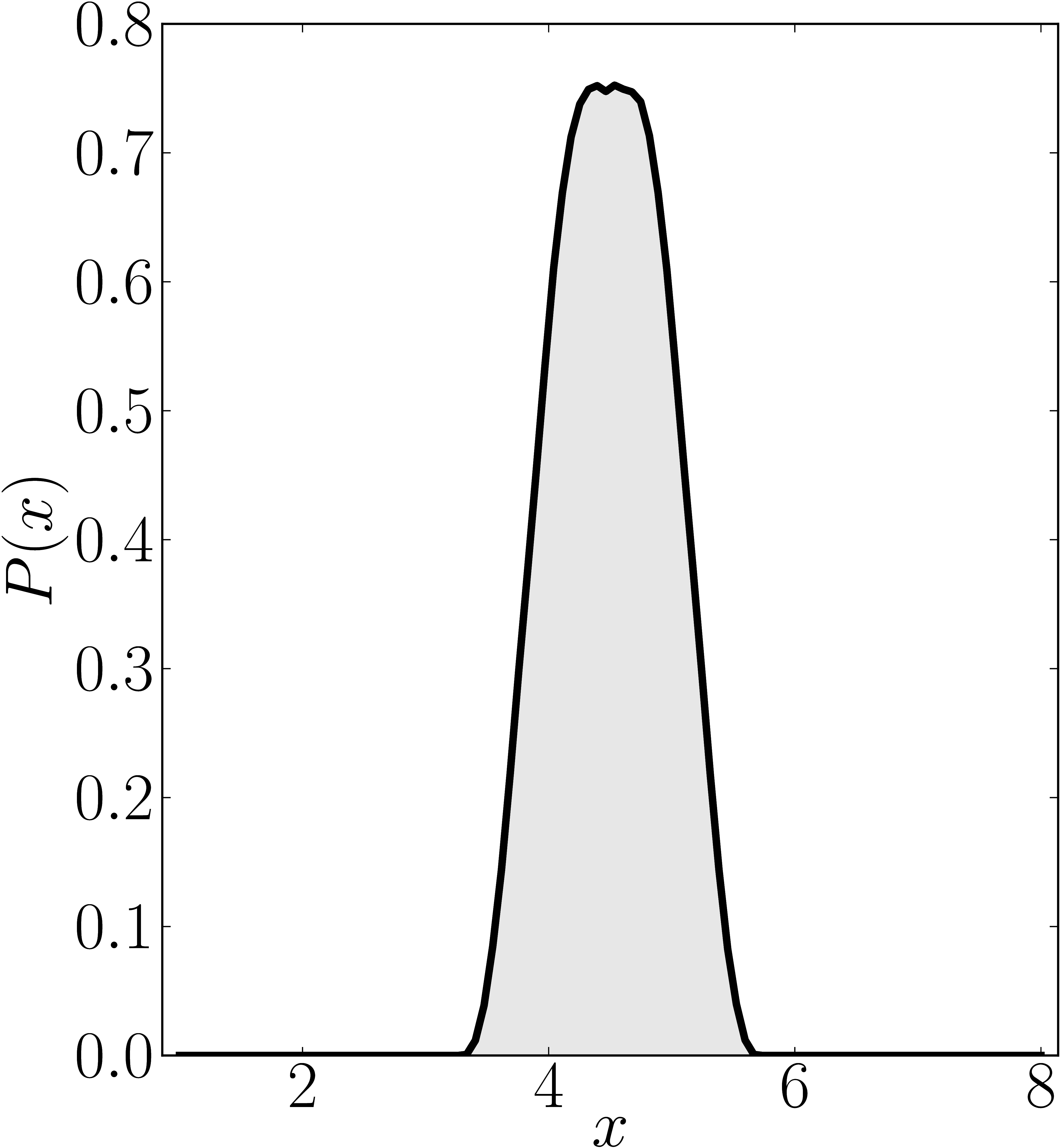
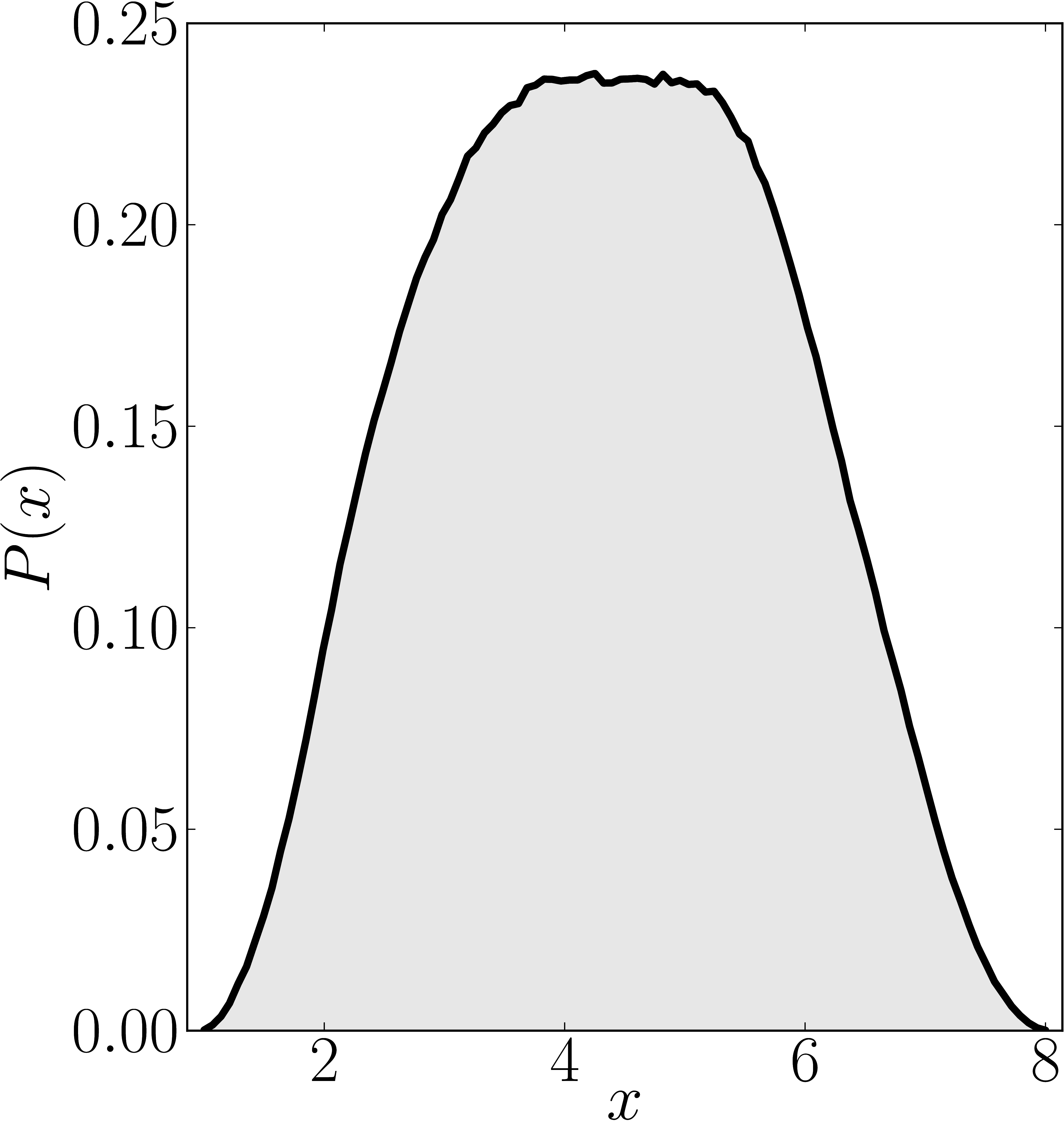
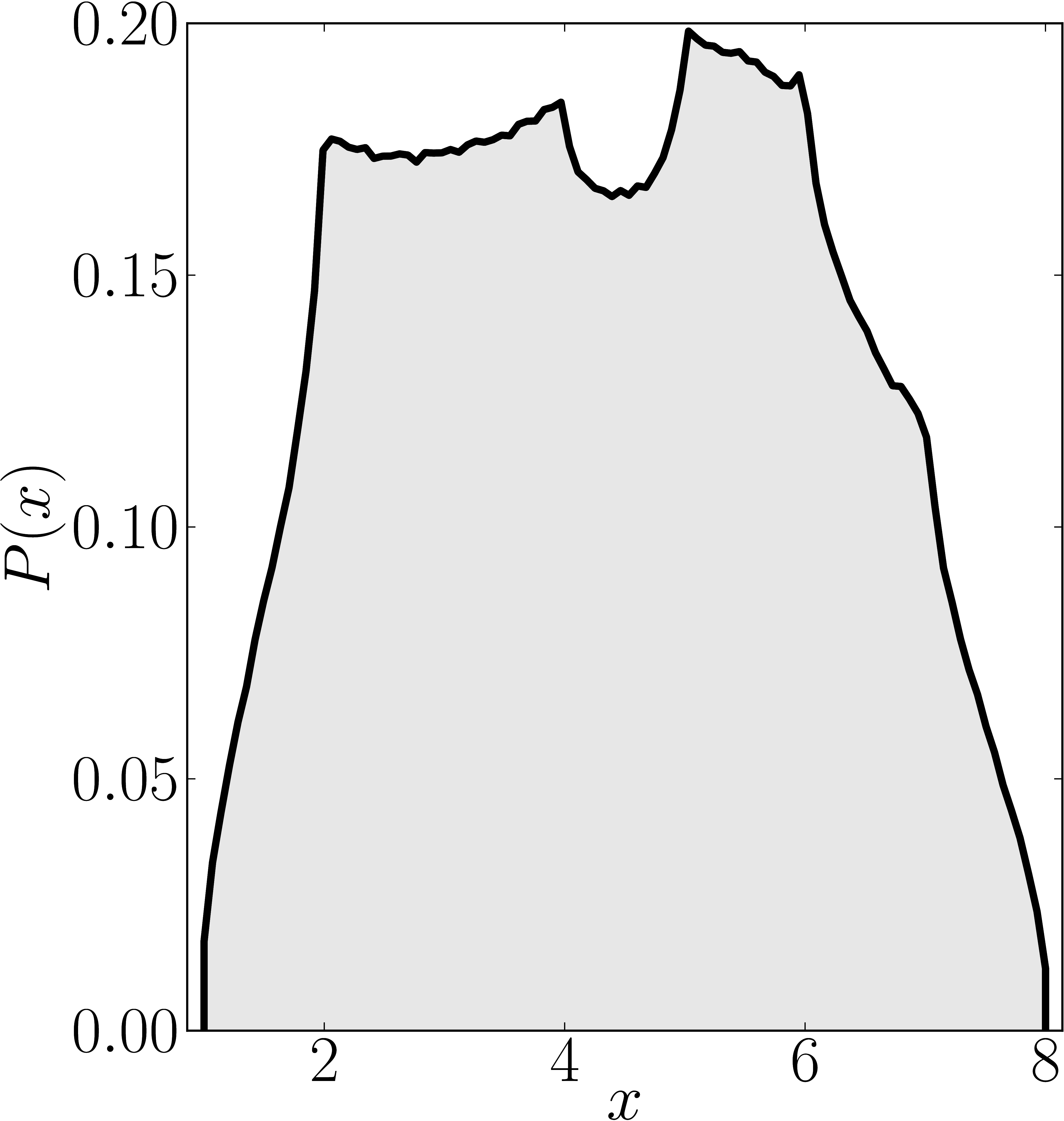
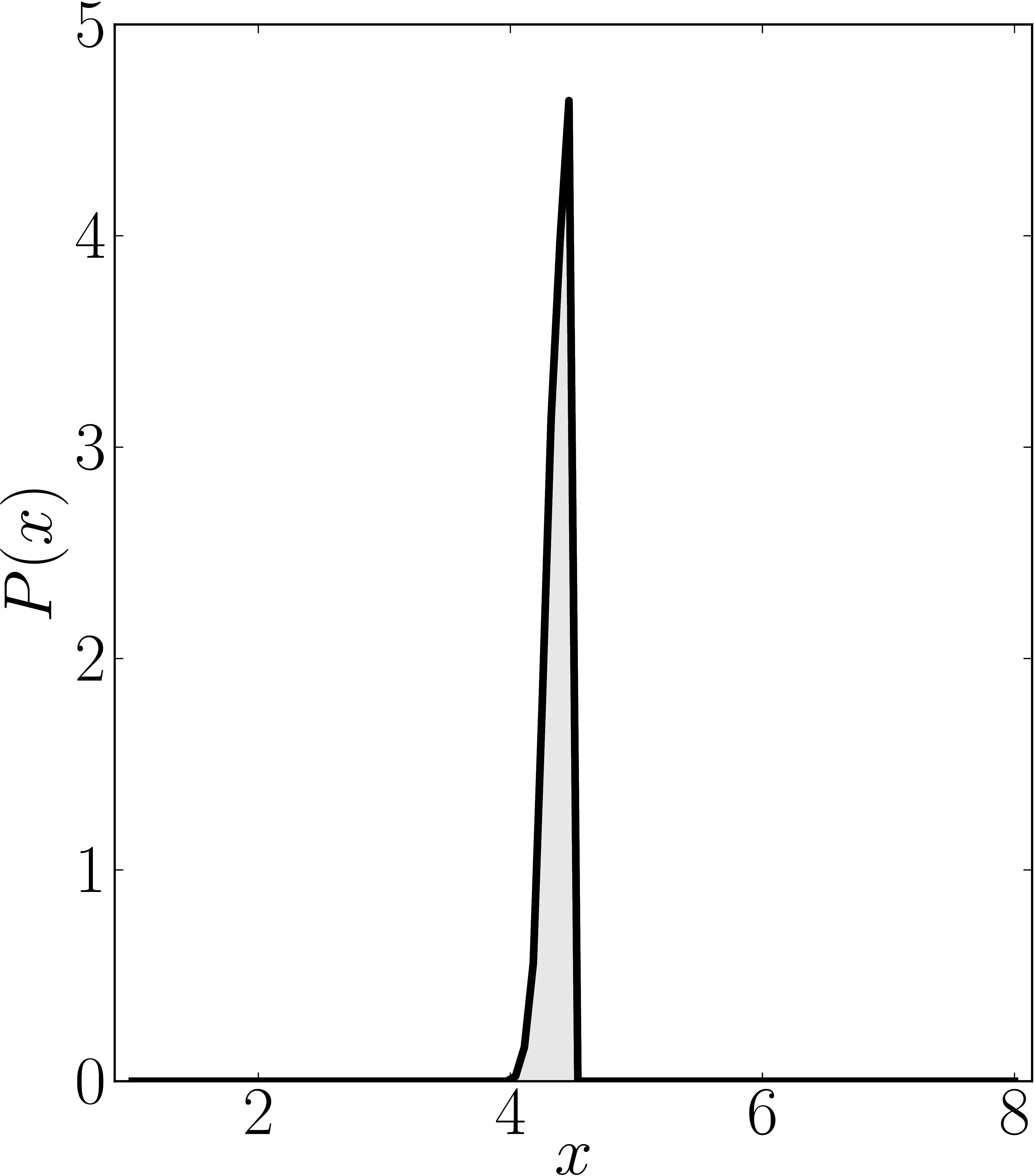
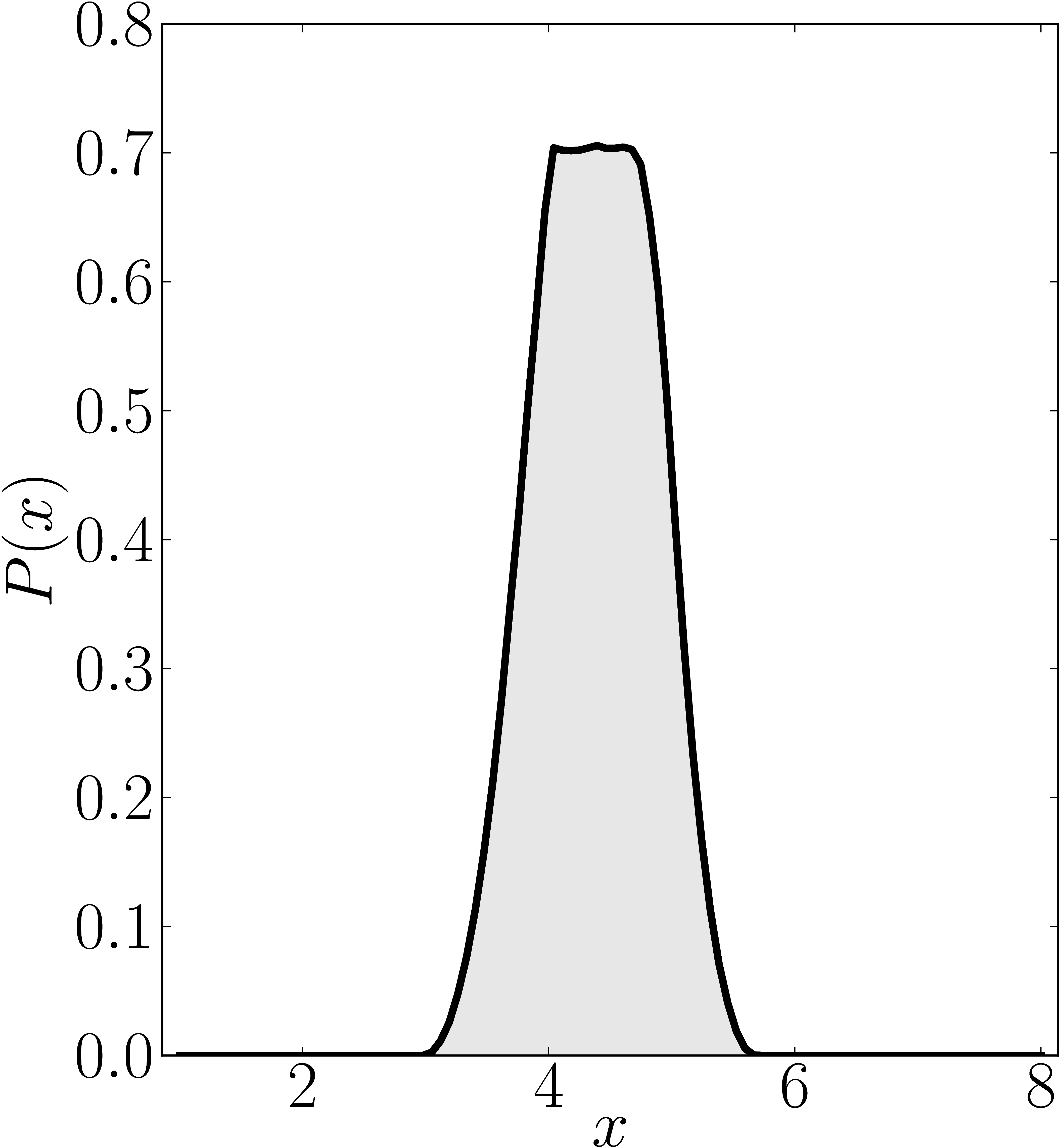
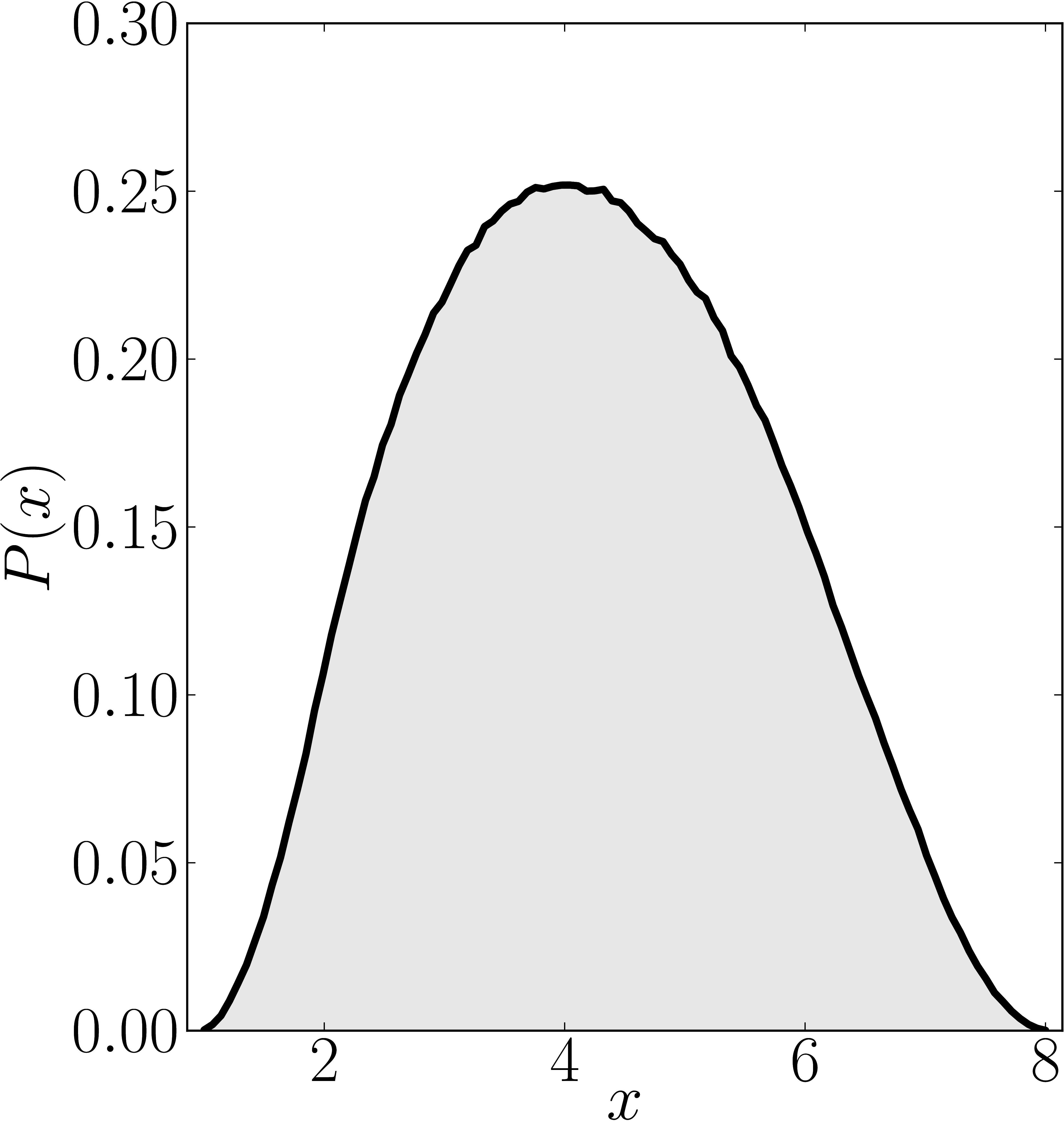
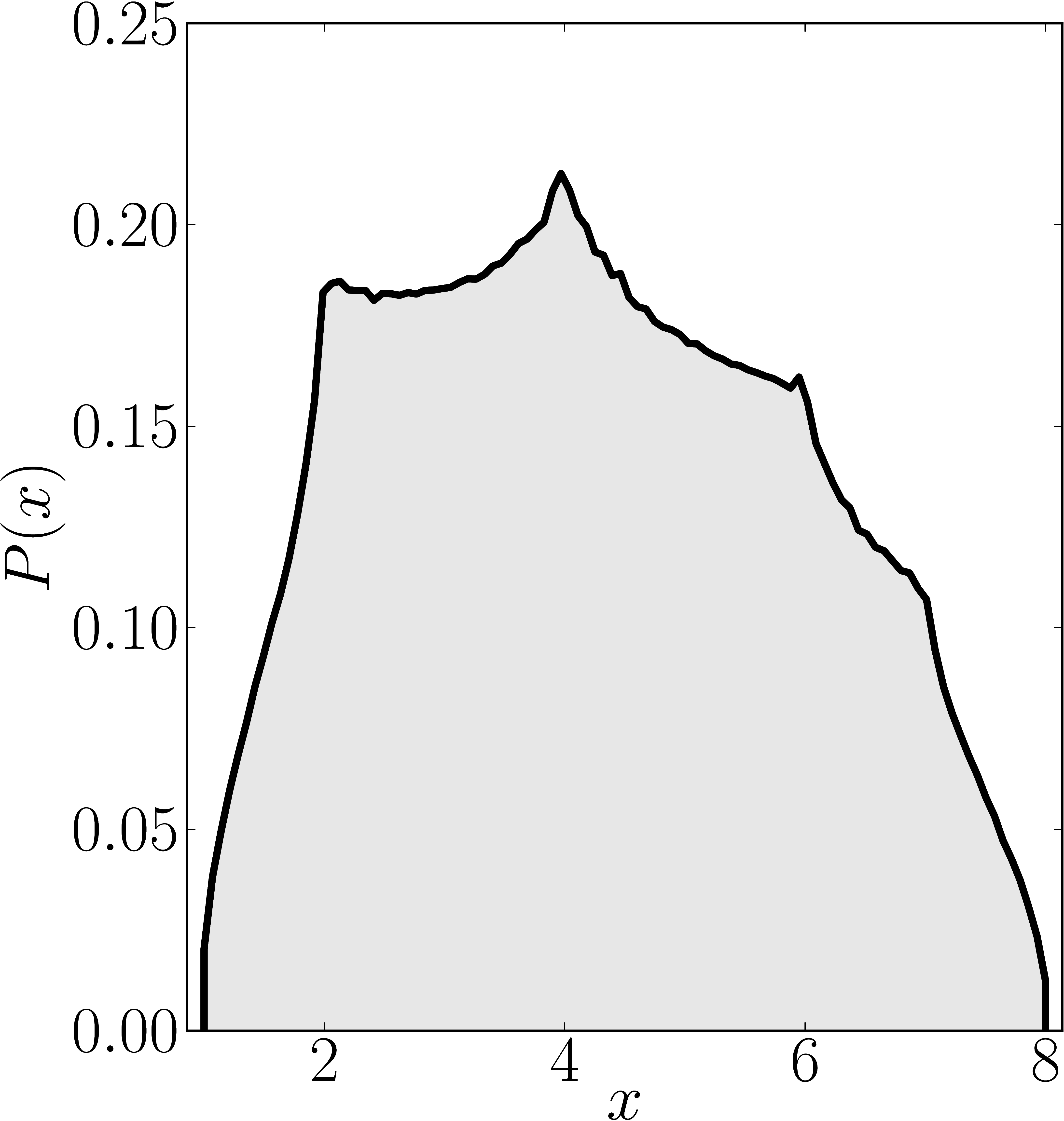
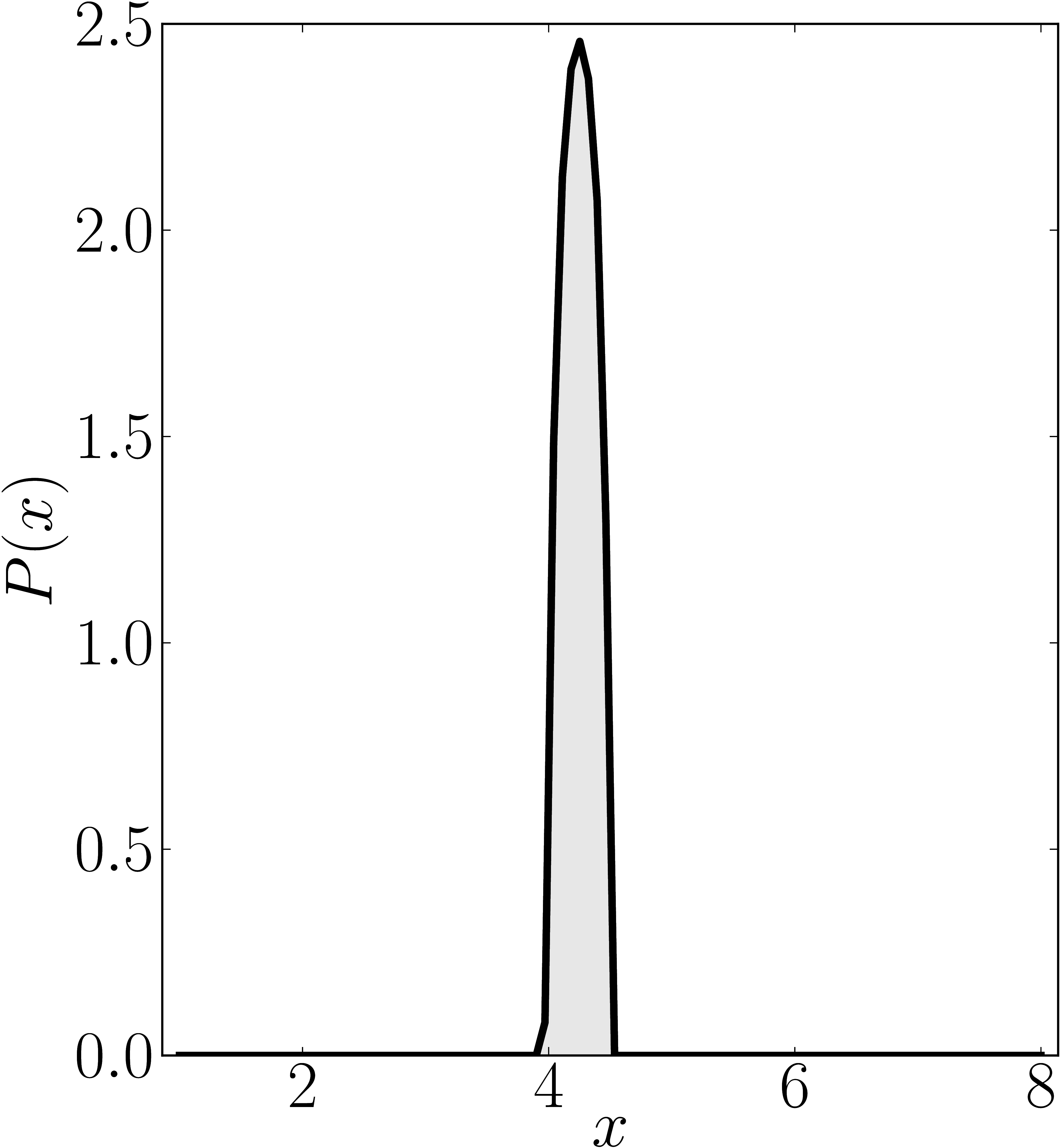
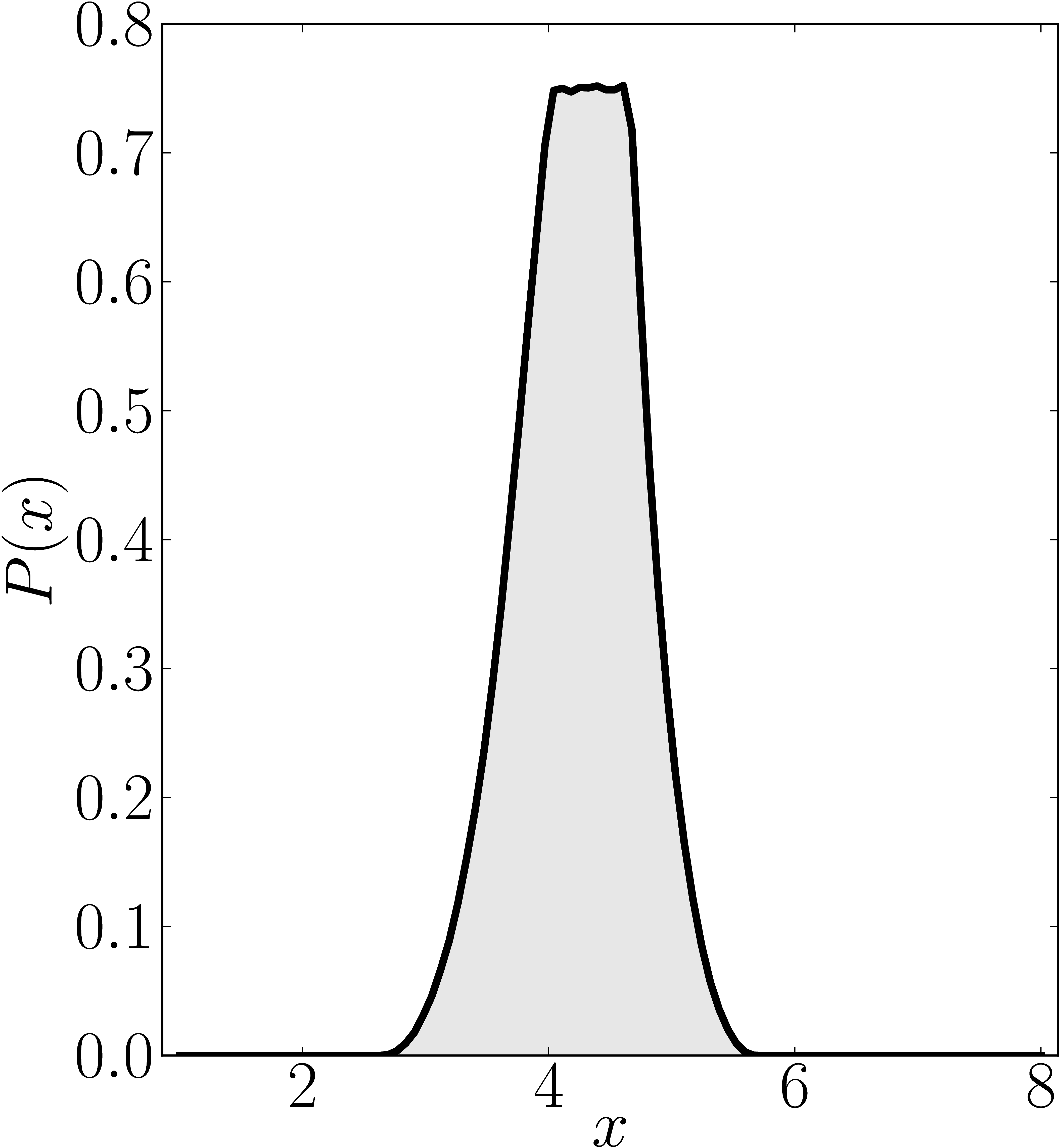
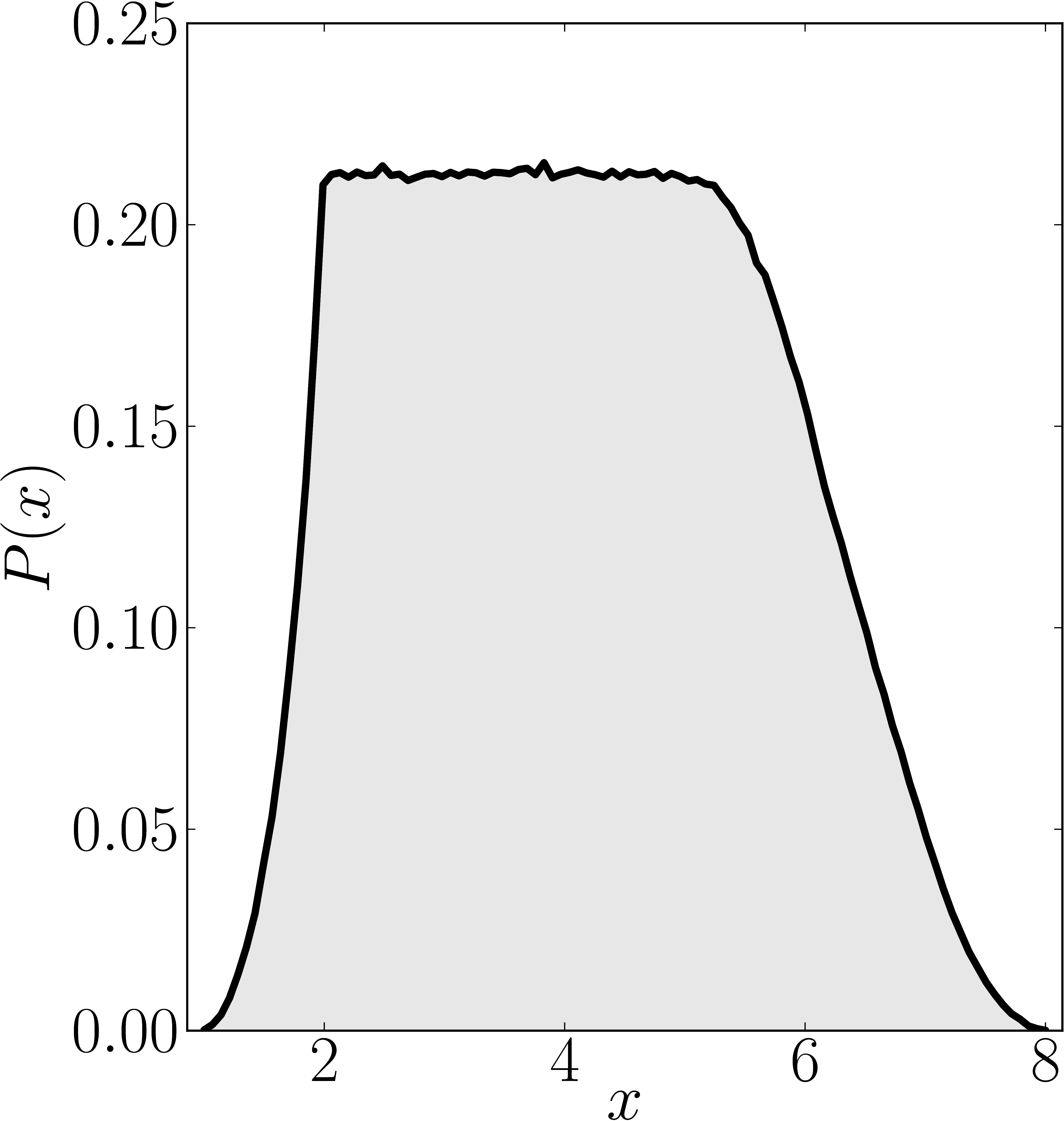
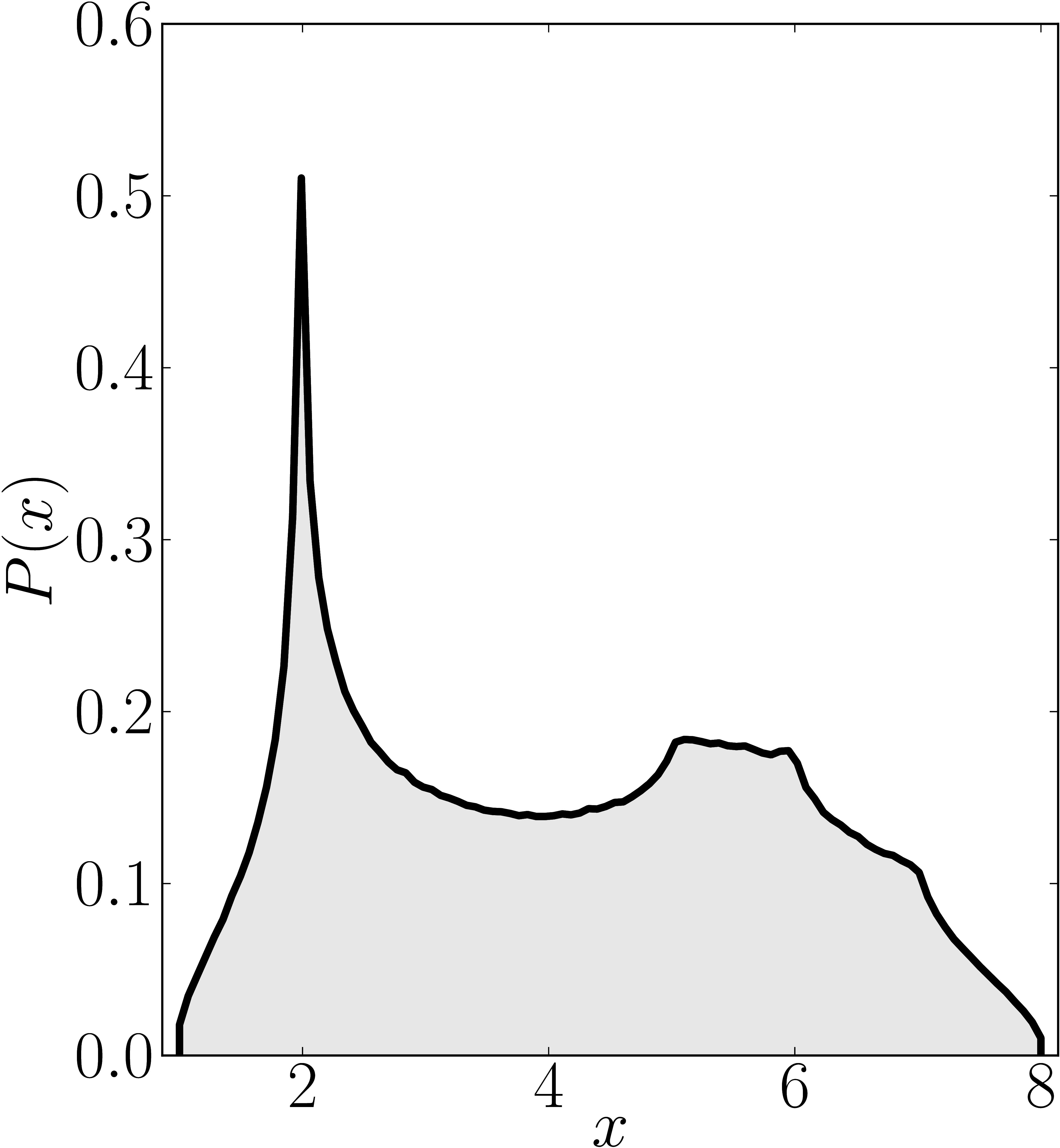
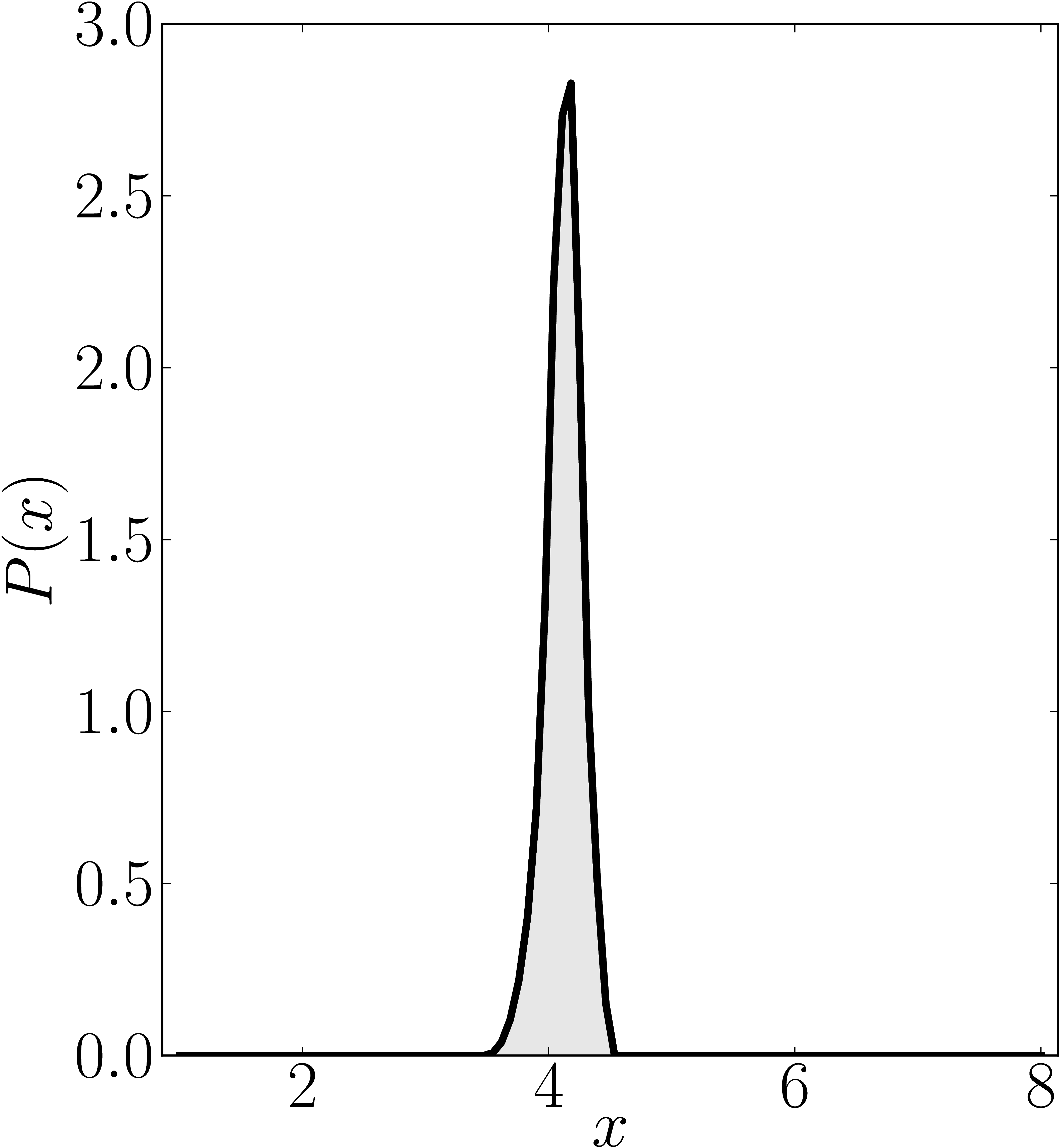
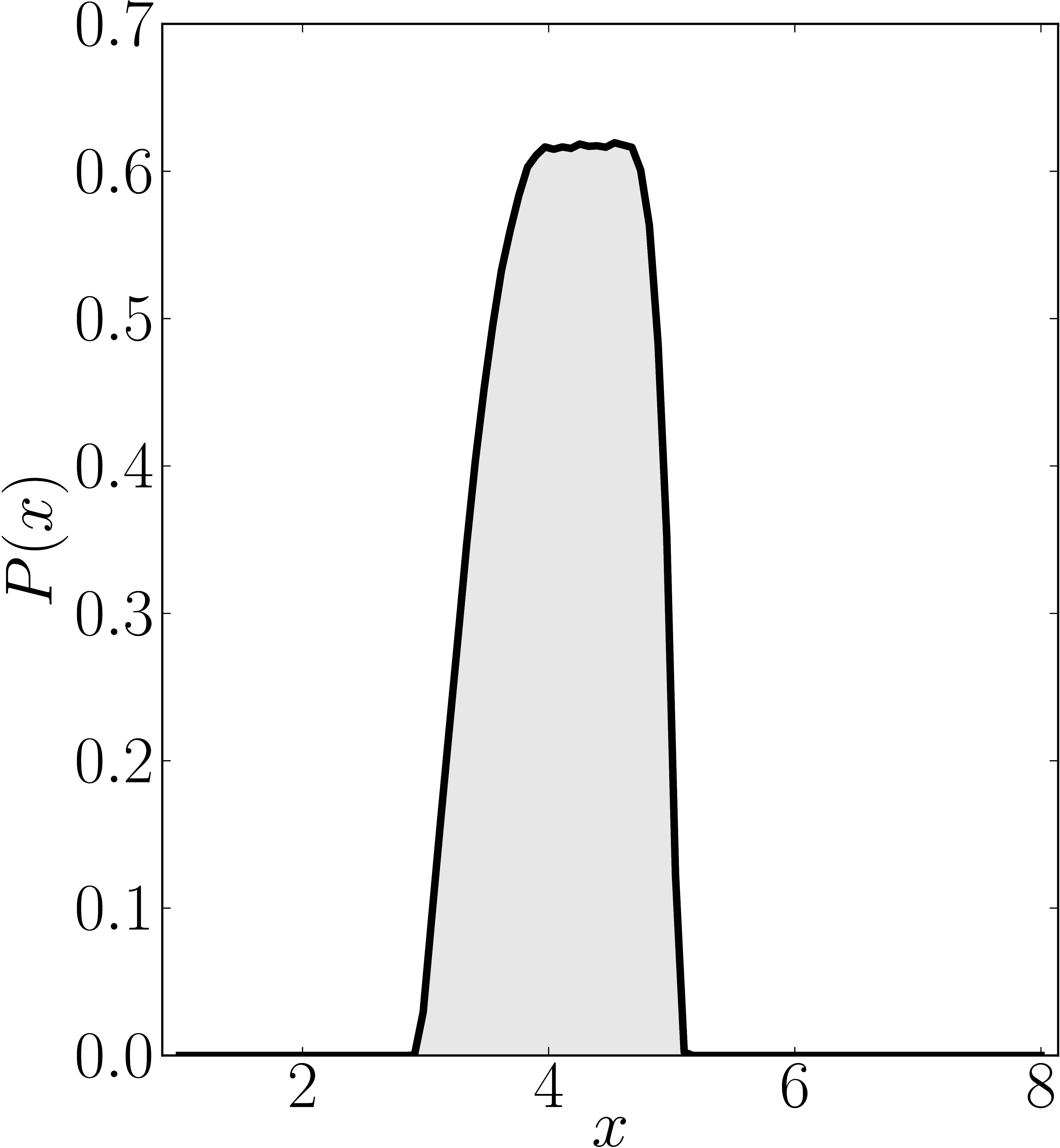
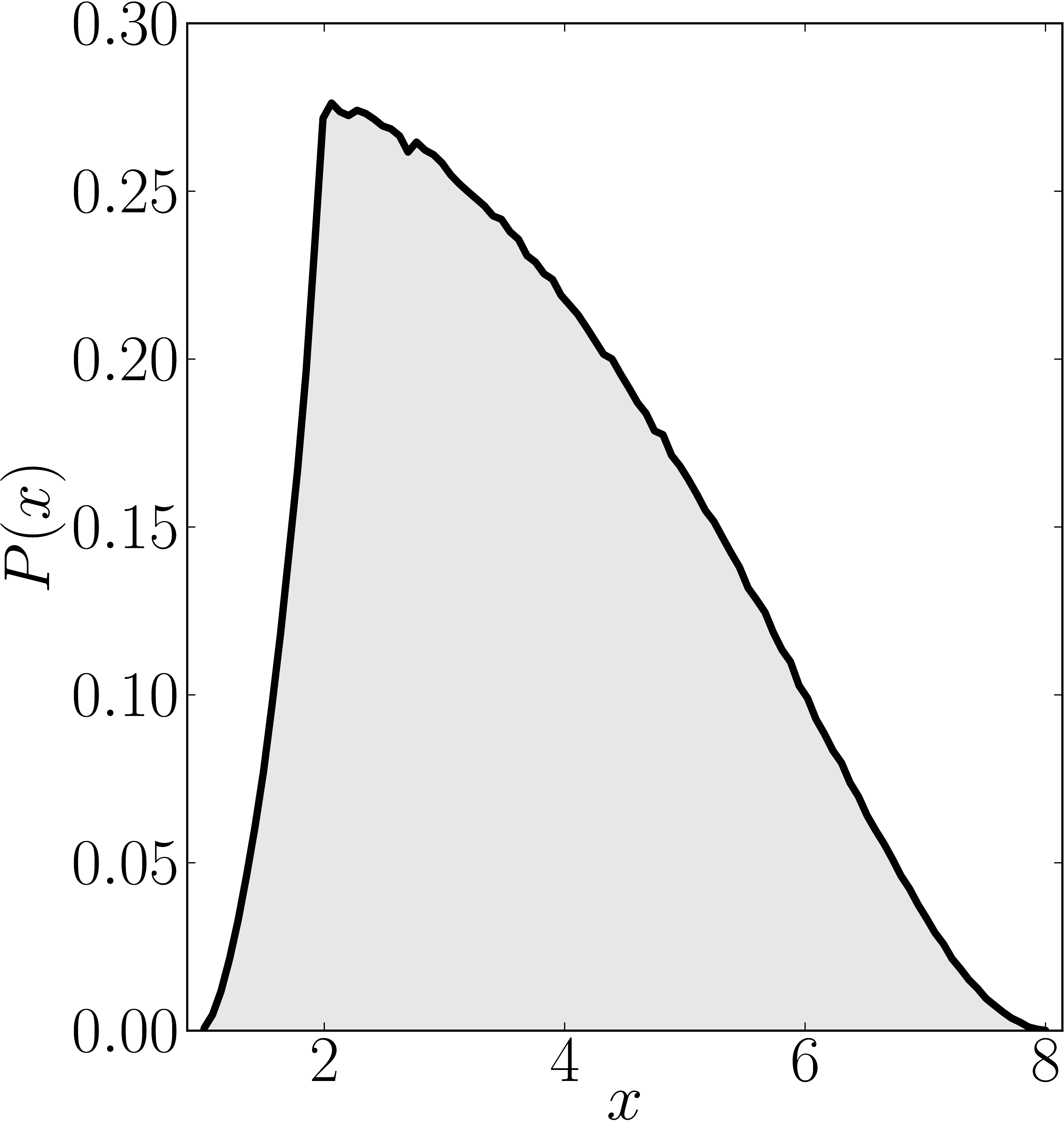
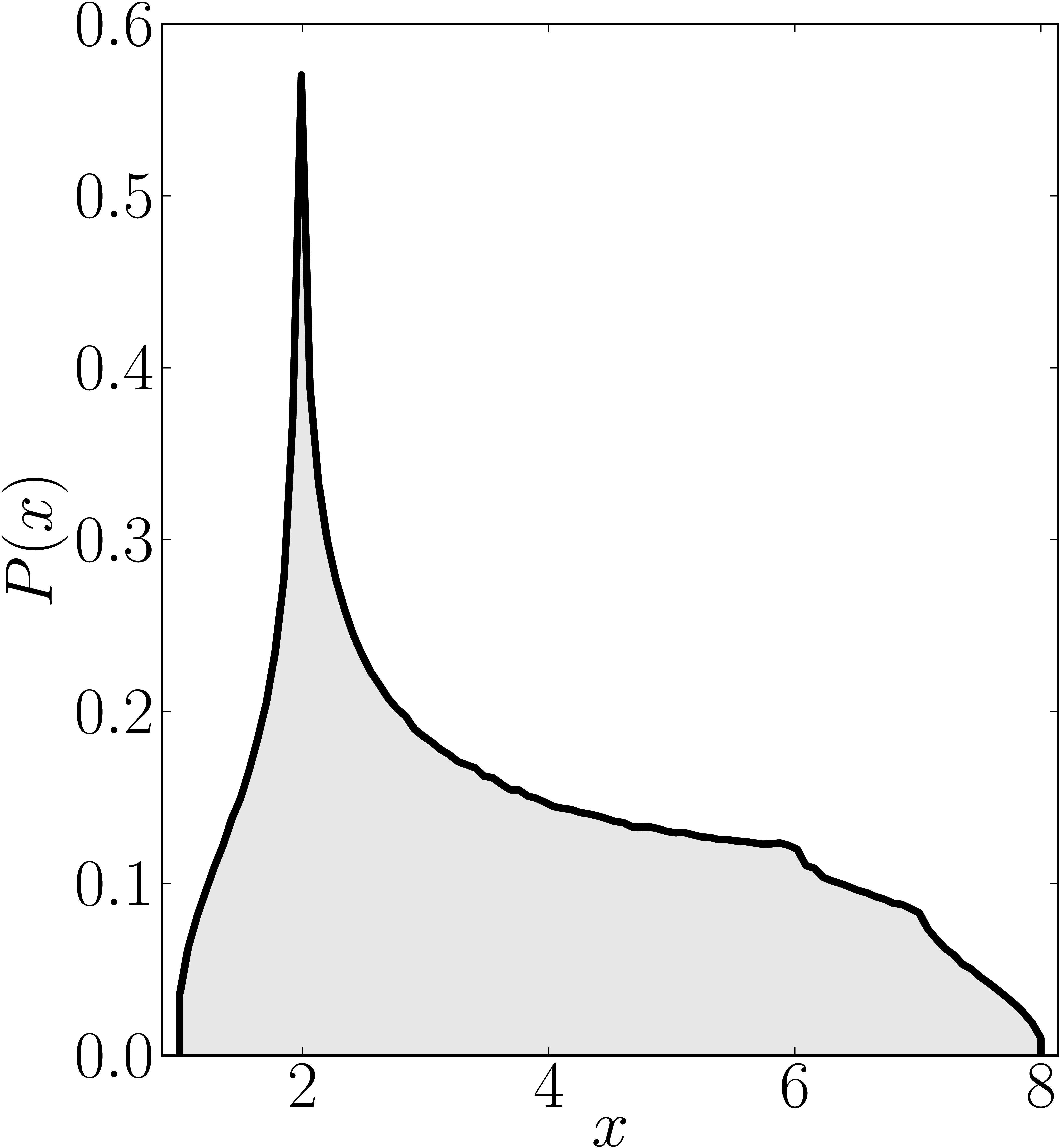
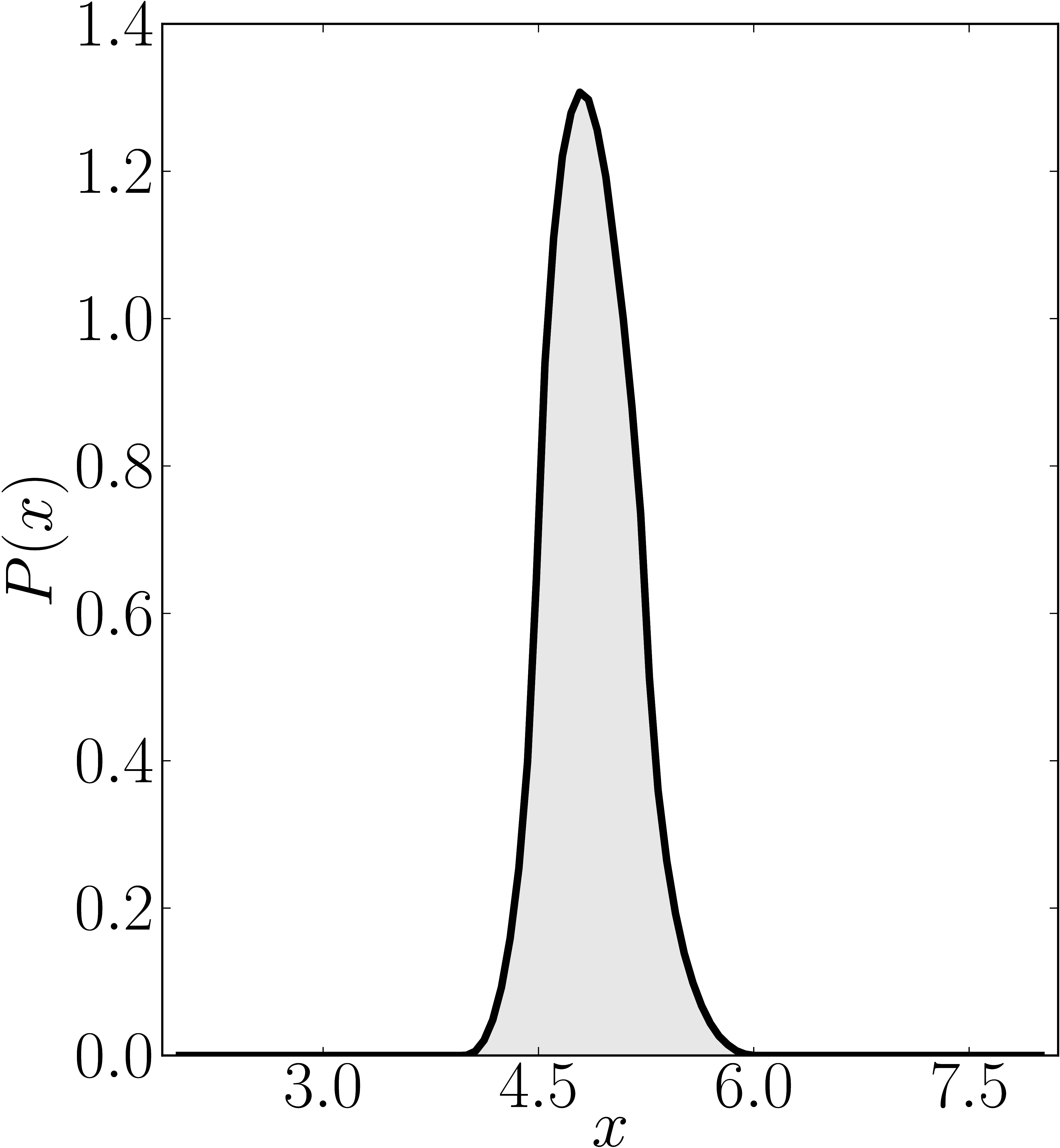
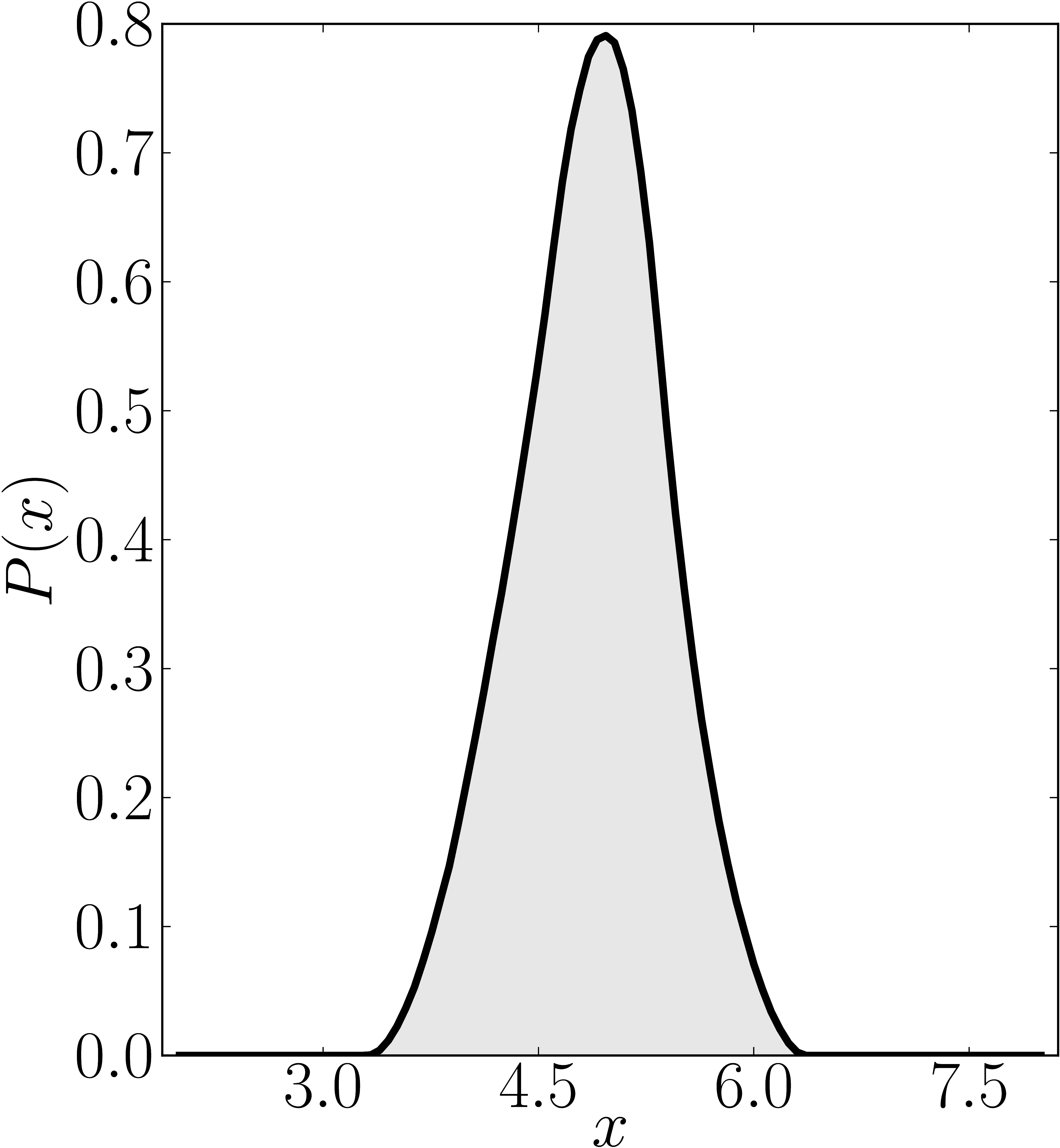
Here we present some example restricted numerical shadow of a 8x8 matrix.

Diagonal matrices

Example 1

The matrix is $\mathrm{diag}(1, \ee^{\frac{2 \ii \pi}{3}}, \ee^{\frac{2 \ii \pi}{3}}, \ee^{\frac{-2 \ii \pi}{3}}, \ee^{\frac{2 \ii \pi}{3}}, \ee^{\frac{02 \ii \pi}{3}}, \ee^{\frac{-2 \ii \pi}{3}} 1)$. We present the (restricted) numerical shadow for the following cases:

1. all pure states (standard shadow), separately for complex and real states
2. product states (product shadow), $\ket{\psi}_\mathrm{sep} = U_A \otimes U_B \otimes U_C \ket{000}$
3. GHZ-entangled states, $\ket{\psi}_\mathrm{GHZ} = U_A \otimes U_B \otimes U_C (\ket{000}+ \ket{111})/\sqrt{2}$, separately for complex and real states
4. so-called W-entangled states, $\ket{\psi}_\mathrm{W} = U_A \otimes U_B \otimes U_C (\ket{100}+ \ket{010}+ \ket{001})/\sqrt{3}$.

Here $U_A$, $U_B$, $U_C$ are independent random unitary matrices sampled from $U(2)$ with respect to the Haar measure.

Example 2

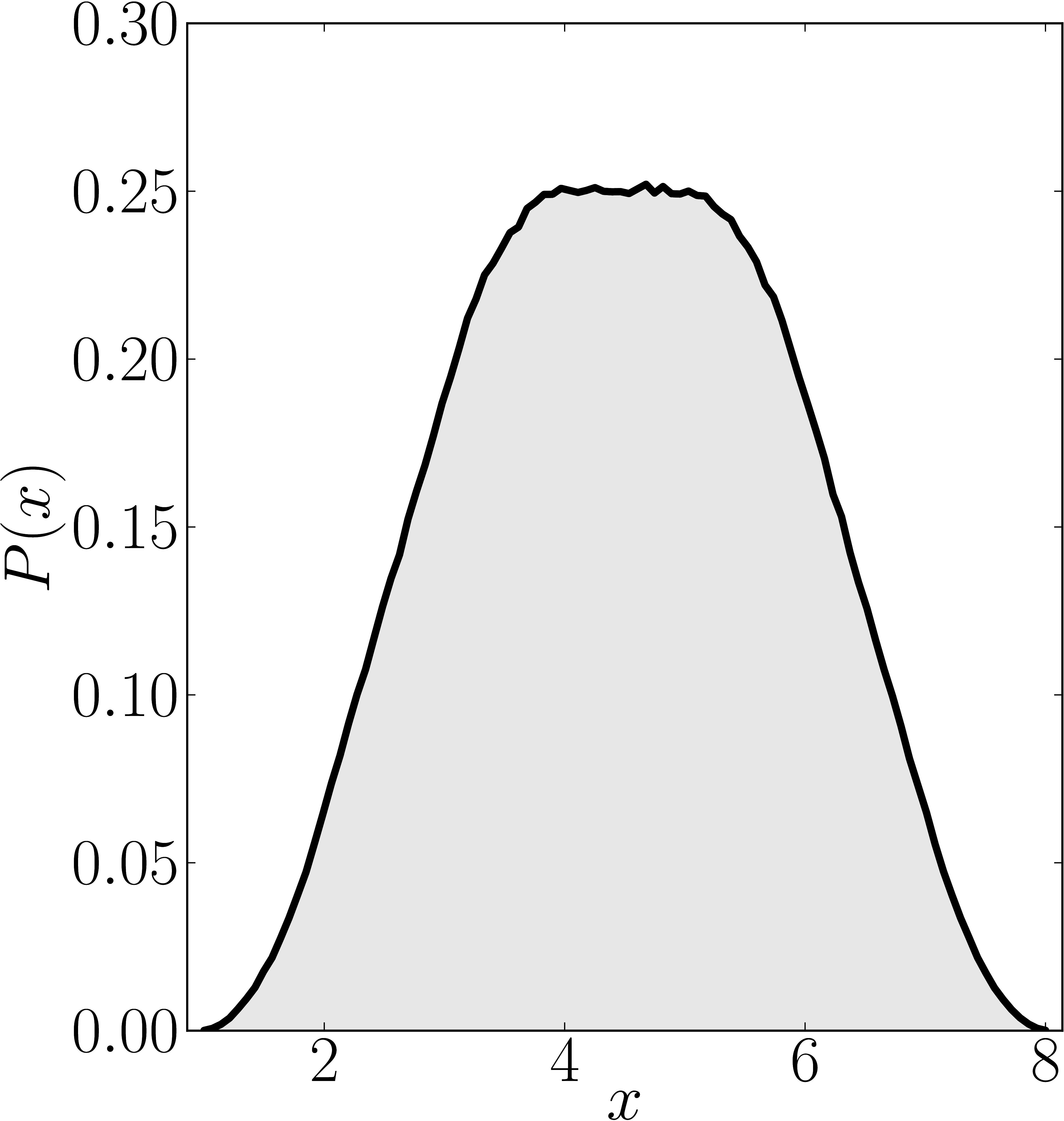
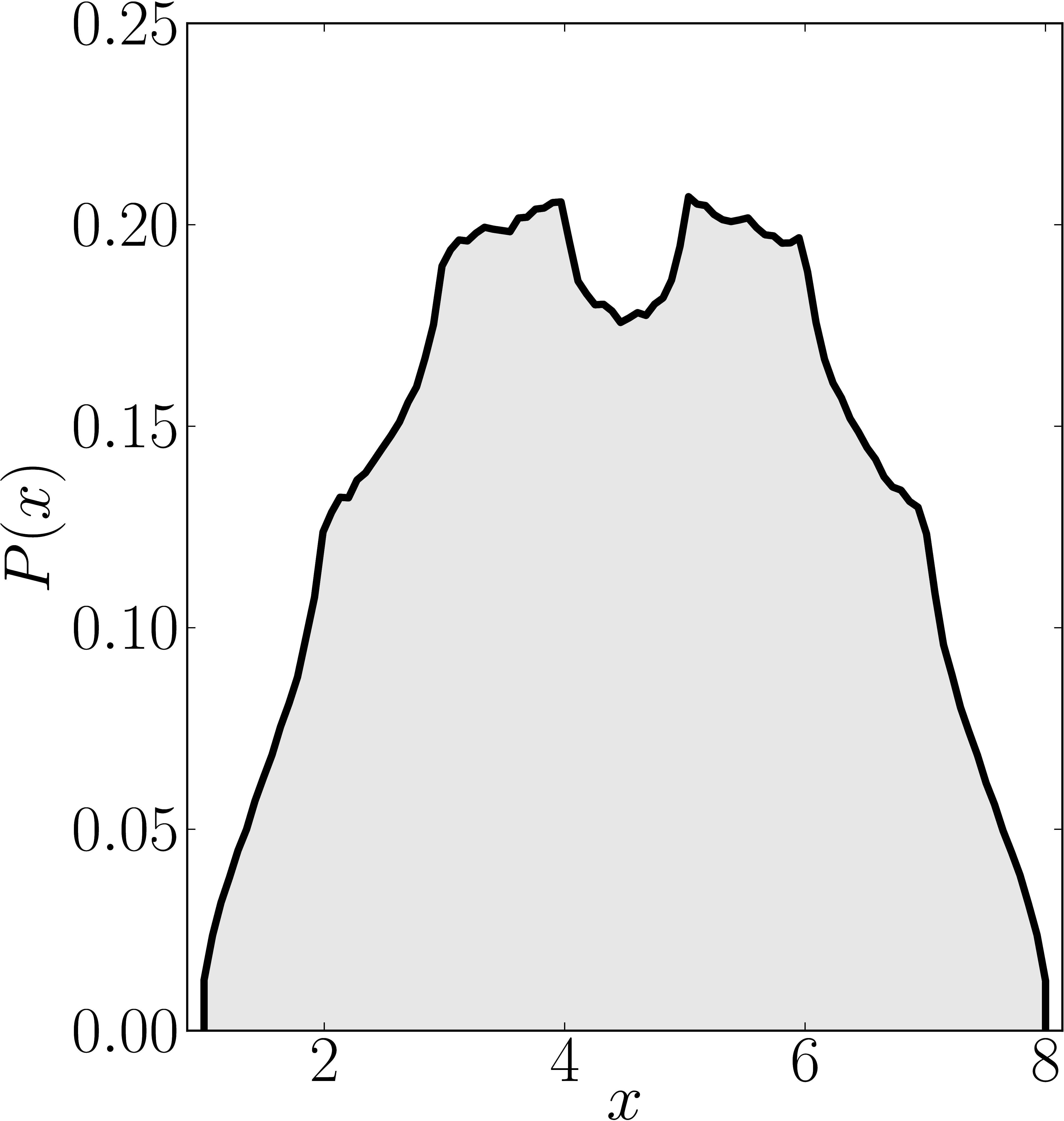
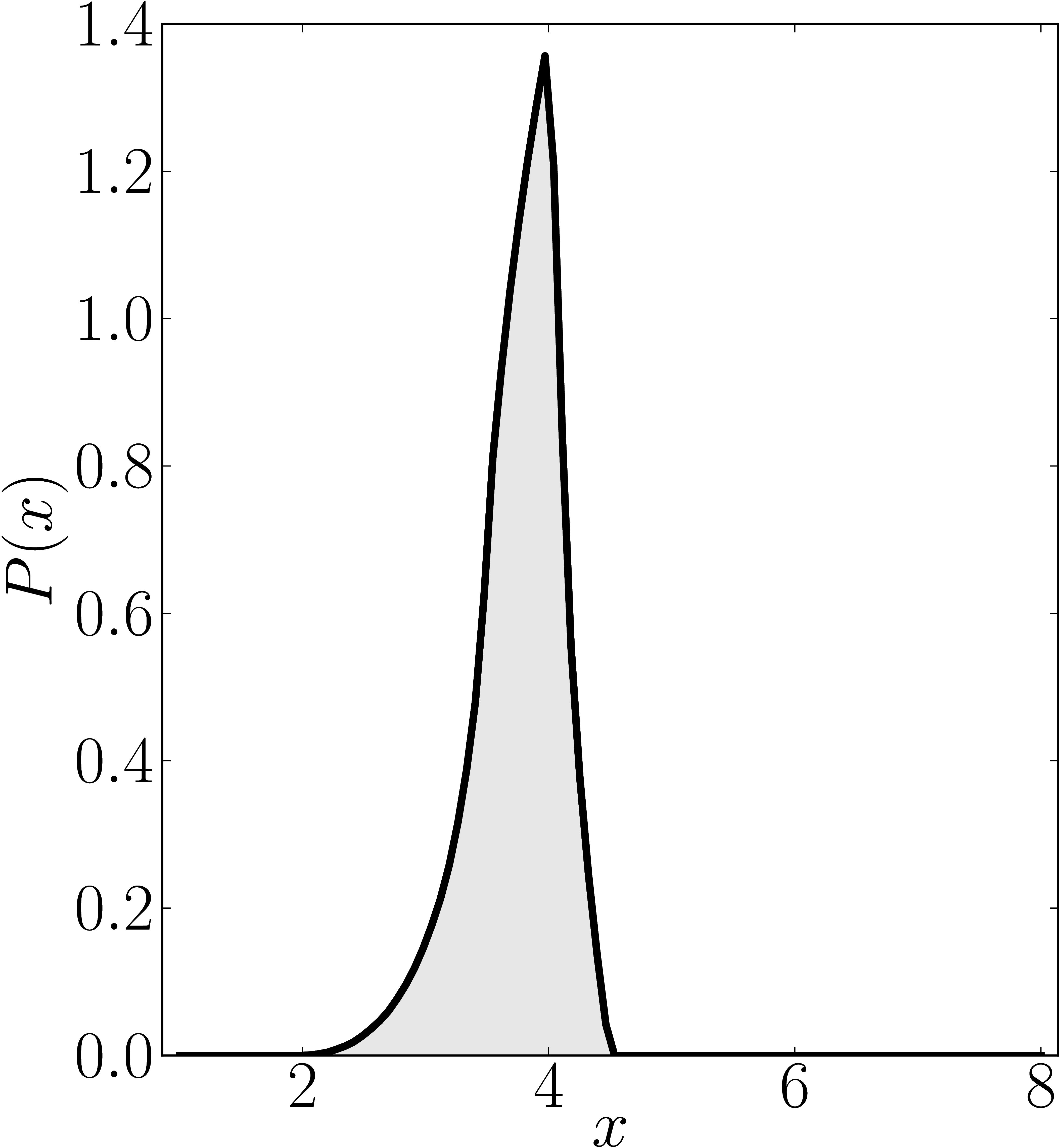
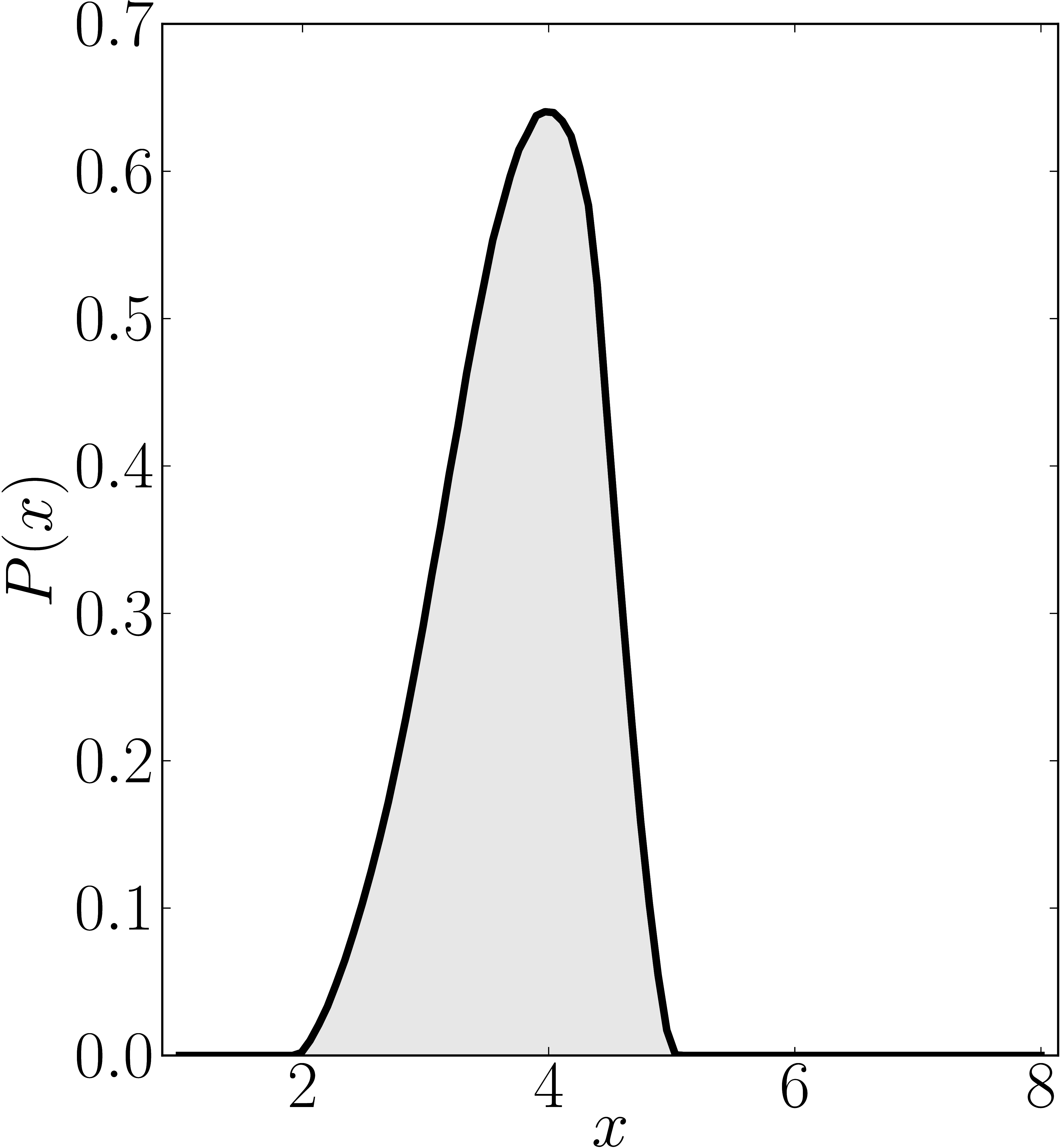
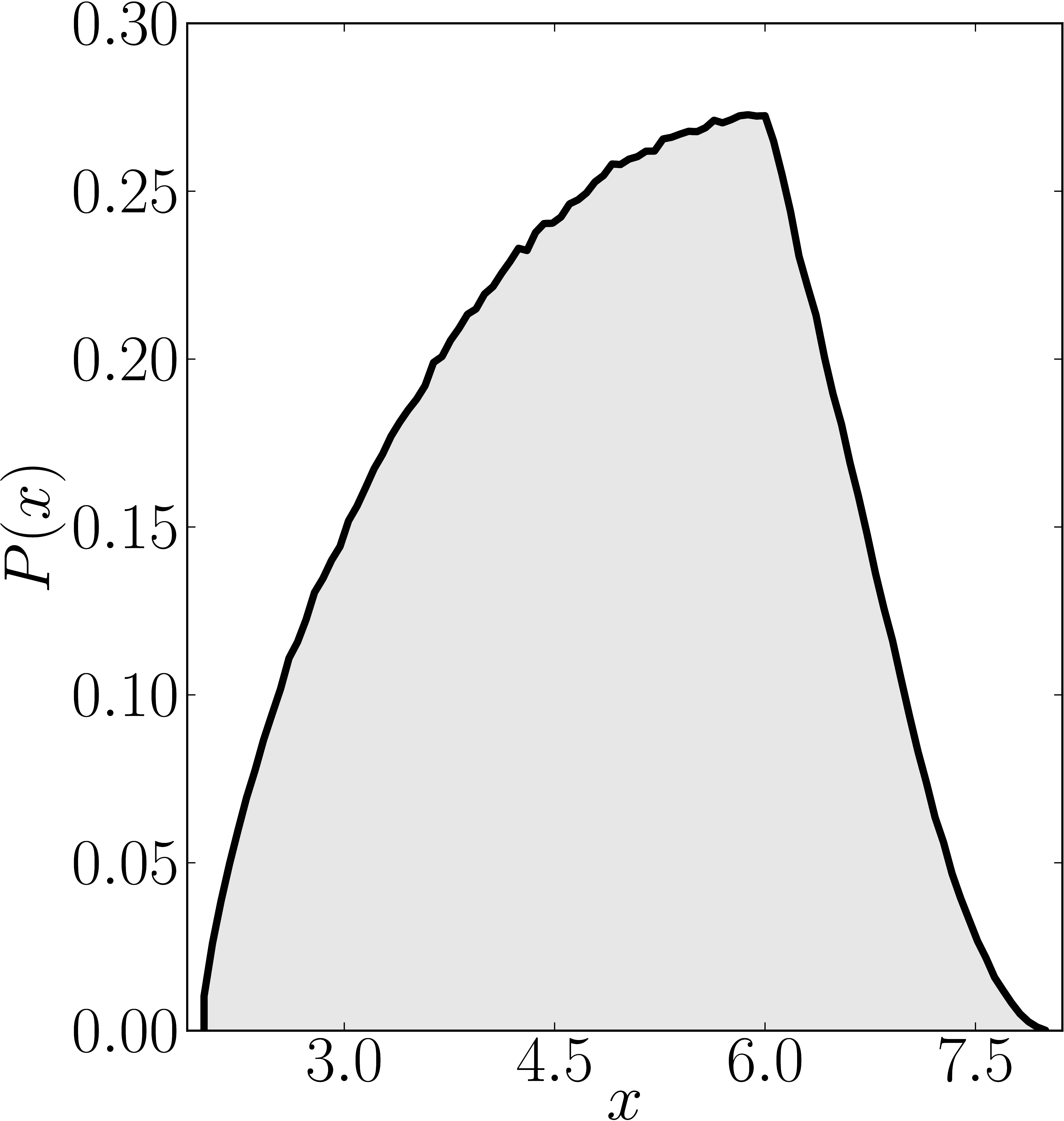
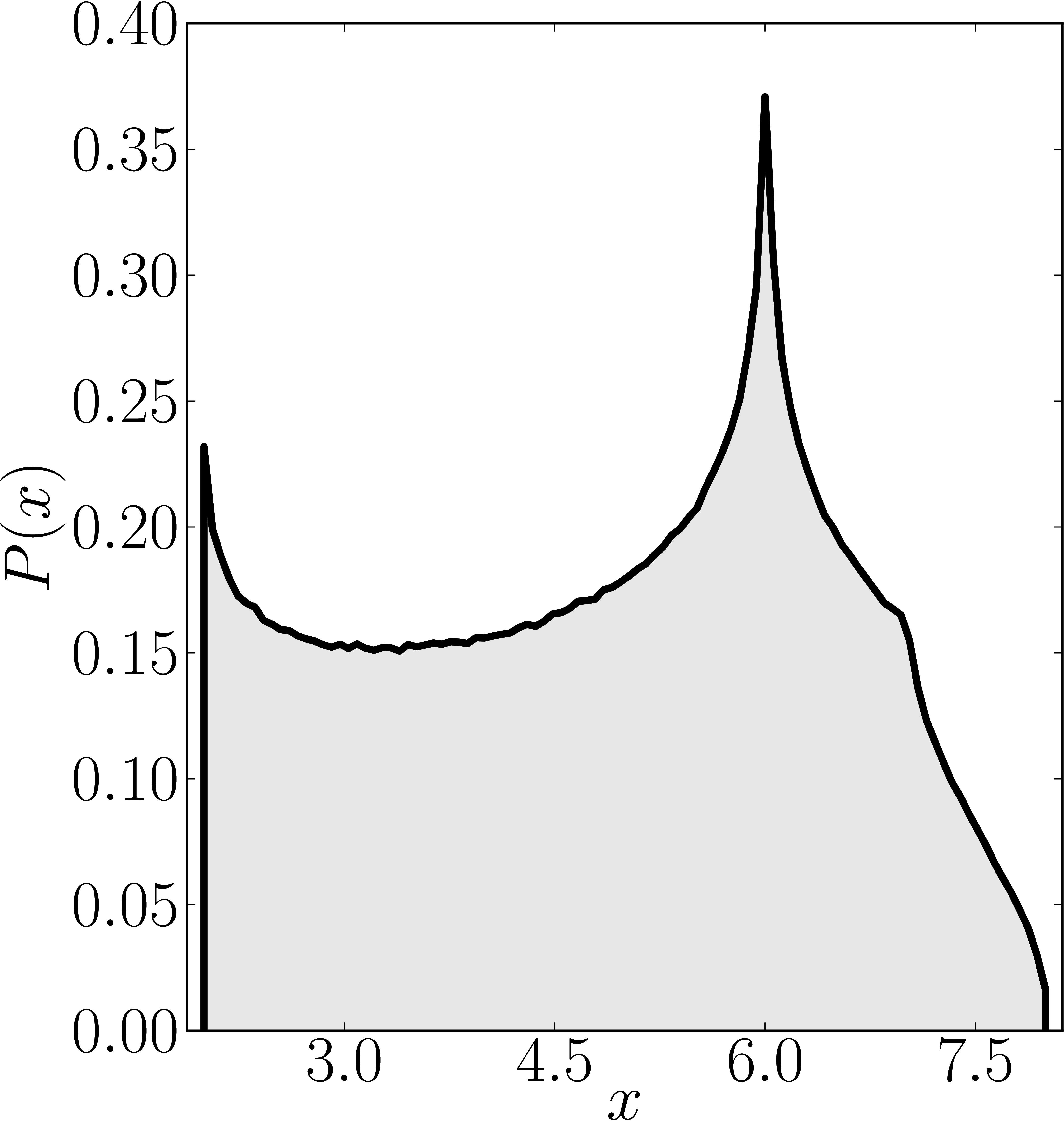
The matrix is $\mathrm{diag}(1,2,3,4,5,6,7,8)$

Example 3

The matrix is $\mathrm{diag}(1,2,2,4,5,6,7,8)$

Example 4

The matrix is $\mathrm{diag}(1,2,2,4,4,6,7,8)$

Example 5

The matrix is $\mathrm{diag}(1,2,2,2,5,6,7,8)$

Example 6

The matrix is $\mathrm{diag}(1,2,2,2,2,6,7,8)$

Example 7

The matrix is $\mathrm{diag}(2,2,2,6,6,6,7,8)$