Hermitian matrices
In the case of Hermitian matrices the numerical shadow is a one dimensional distribution.
Diagonal matrices
Example 1
The matrix is $\mathrm{diag}(0,6)$
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
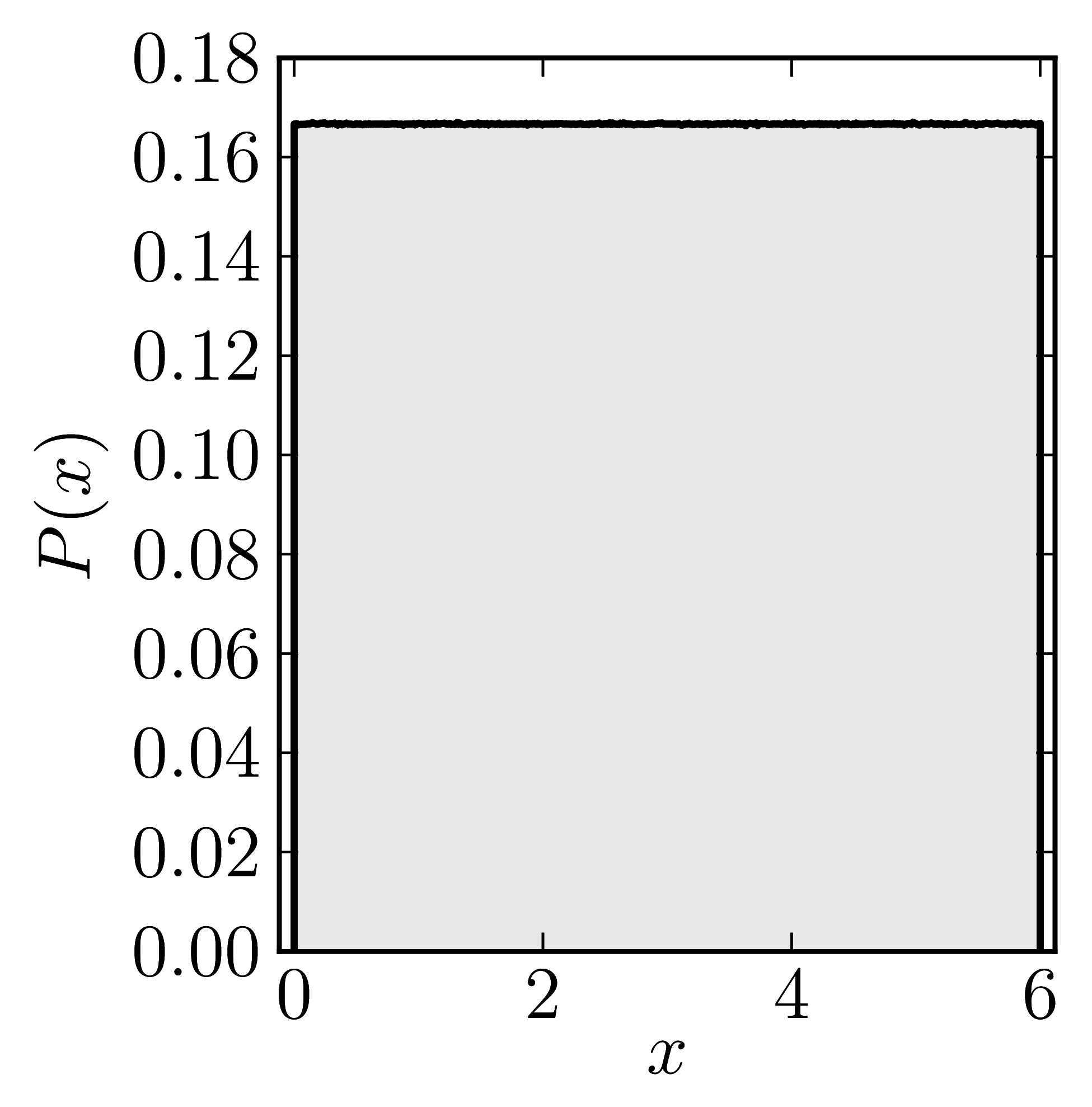 | 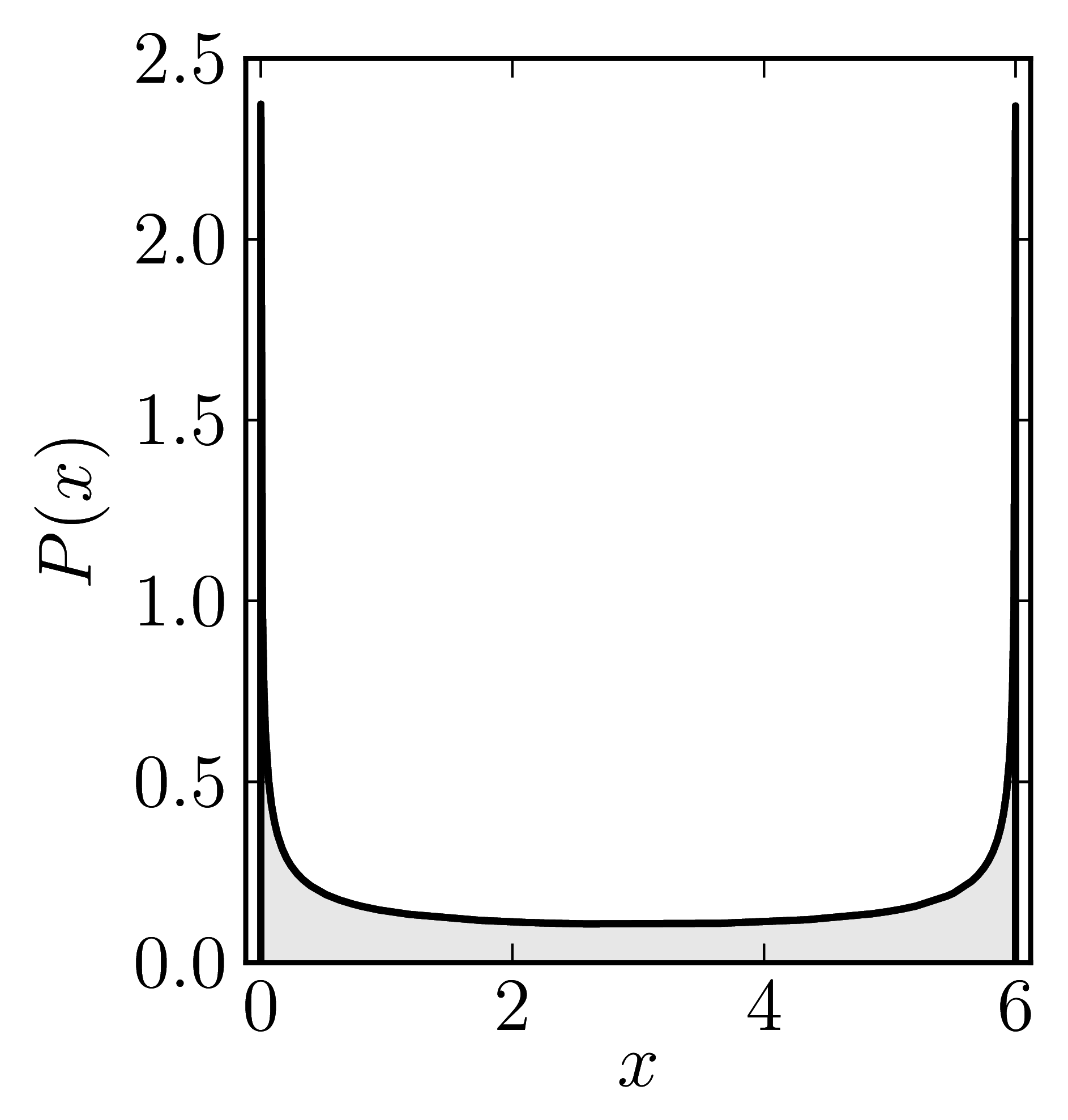 |
Non-normal matrices
Example 1
The matrix is $\begin{pmatrix} 0&1\ 0&0 \end{pmatrix}.$ The shadow resembles a physical shadow cast by the hollow sphere made of transparent material when illuminated by a light source at infinity.
| Standard numerical shadow with respect to complex states | Cross-section of the shadow along the real axis |
|---|---|
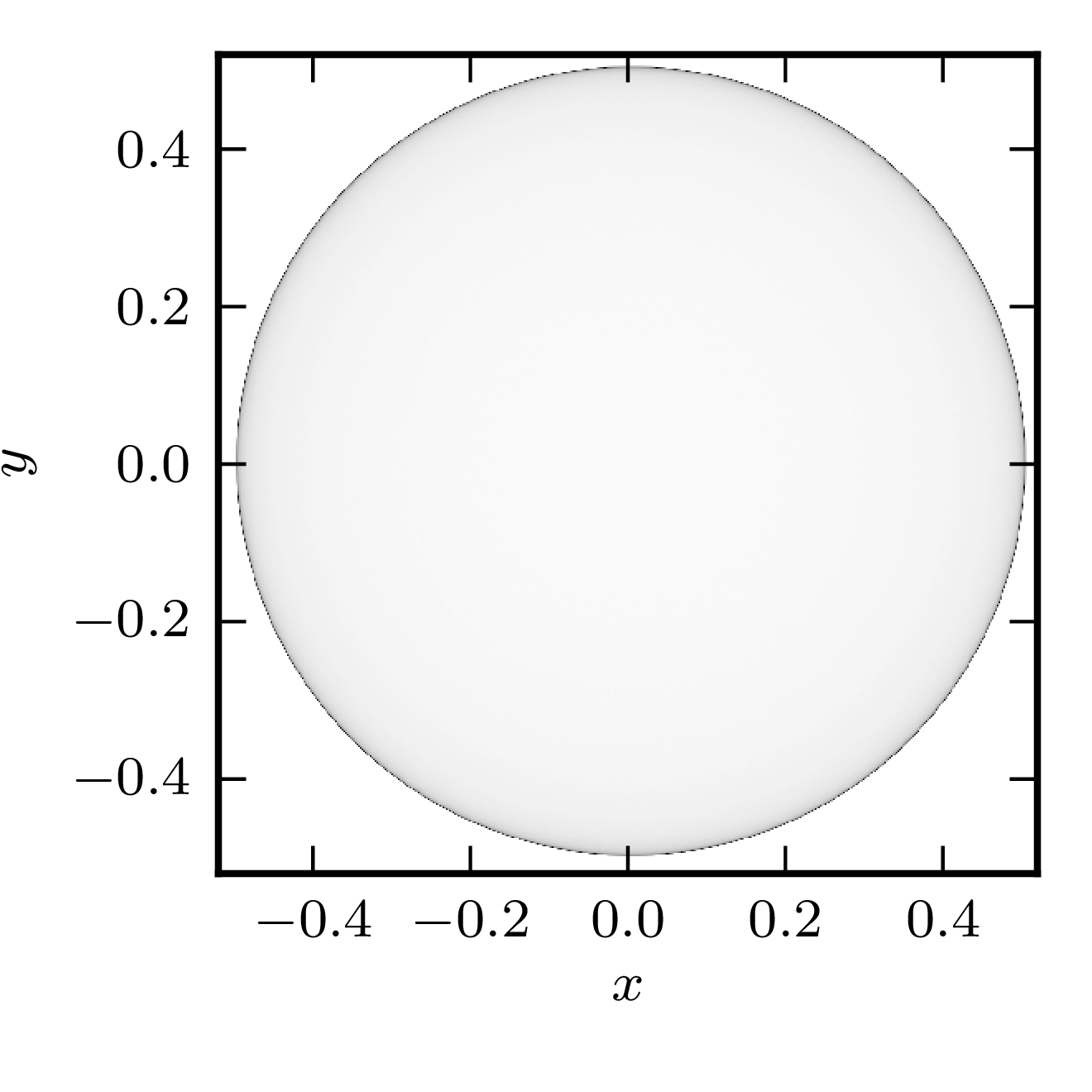 | 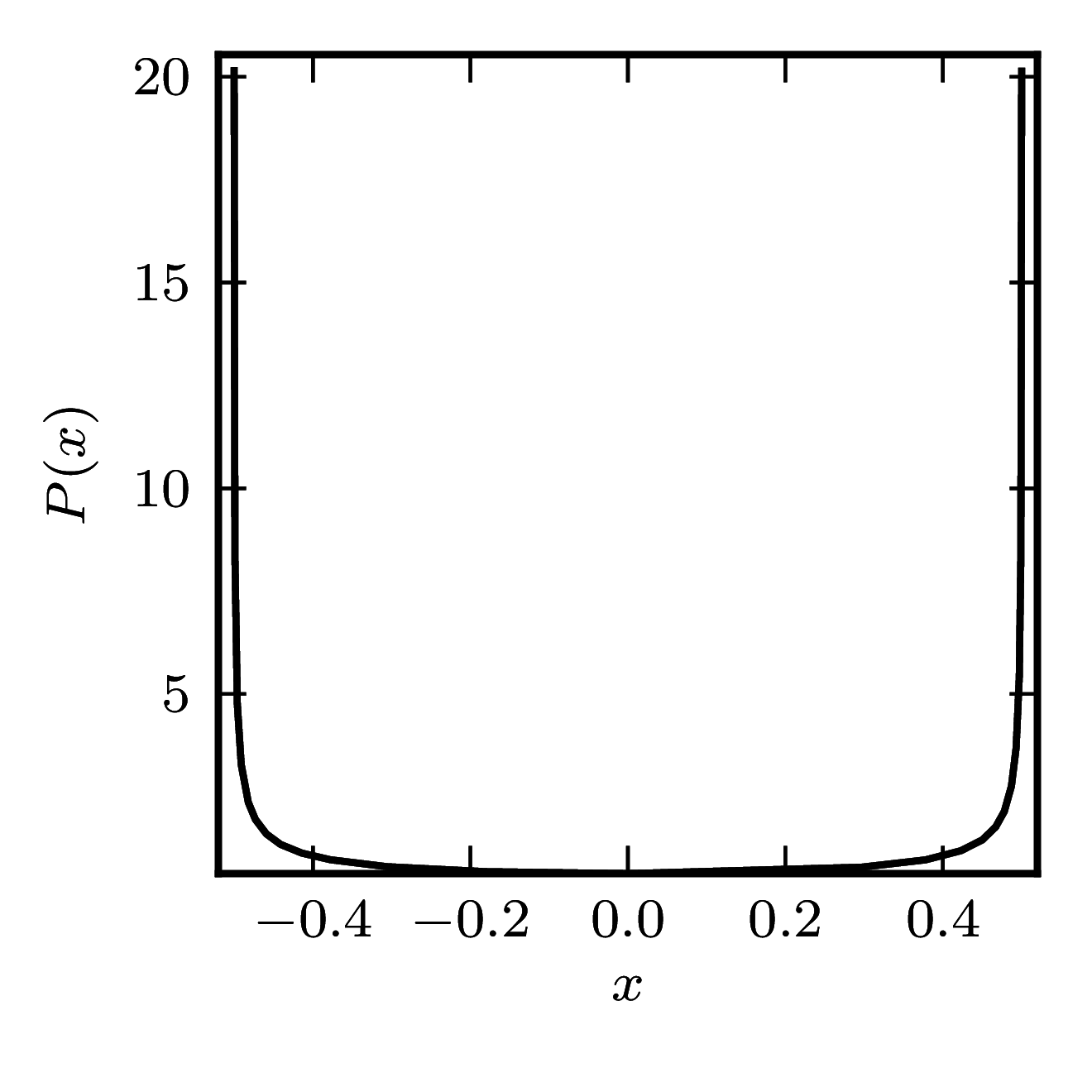 |
Example 2
The matrix is $\begin{pmatrix} 0&1\ 0&1 \end{pmatrix}.$ The shadow resembles physical shadow cast by the hollow sphere made of transparent material when illuminated by a light source at infinity, but with screen not perpendicular to the light rays.
| Standard numerical shadow with respect to complex states | Cross-section of the shadow along the real axis |
|---|---|
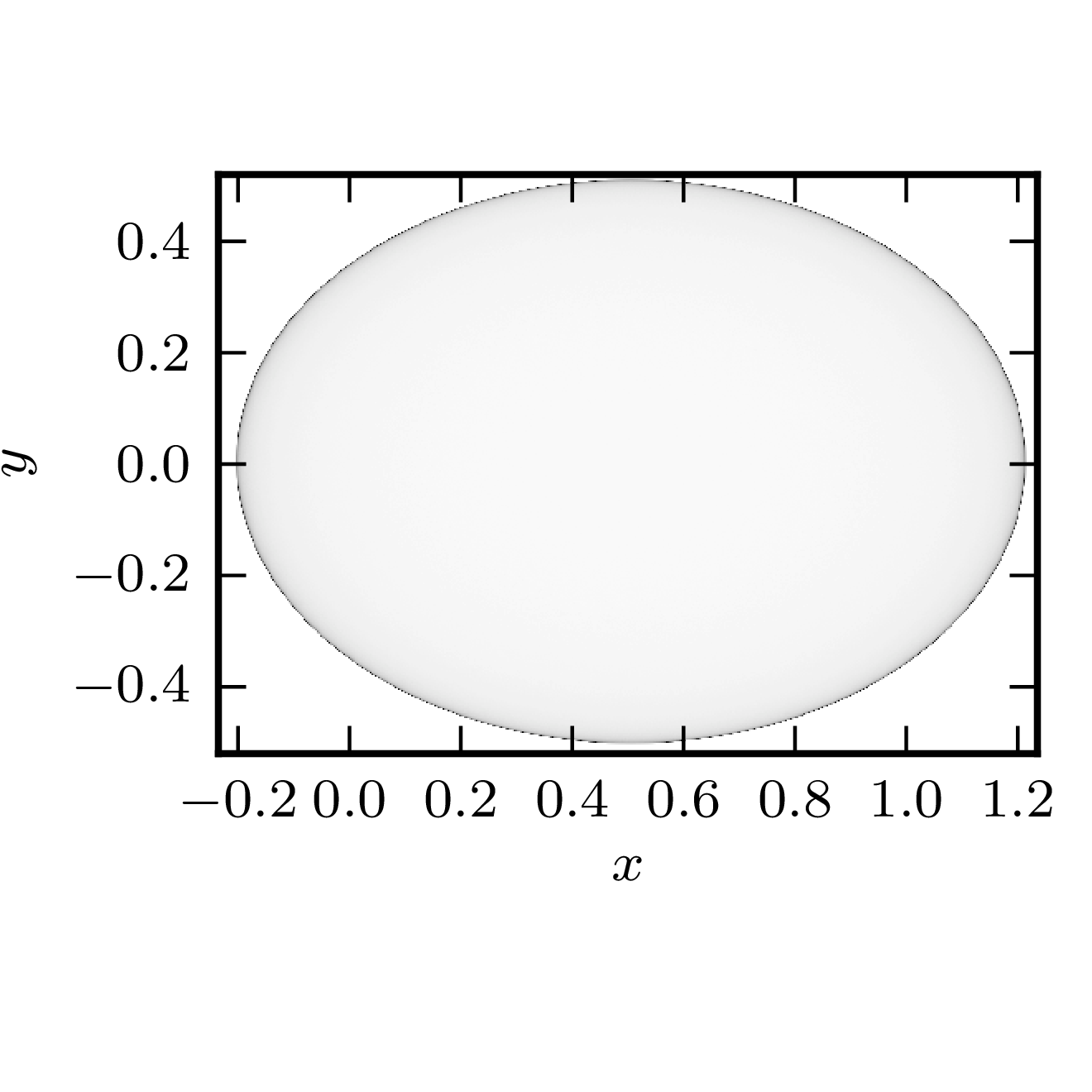 | 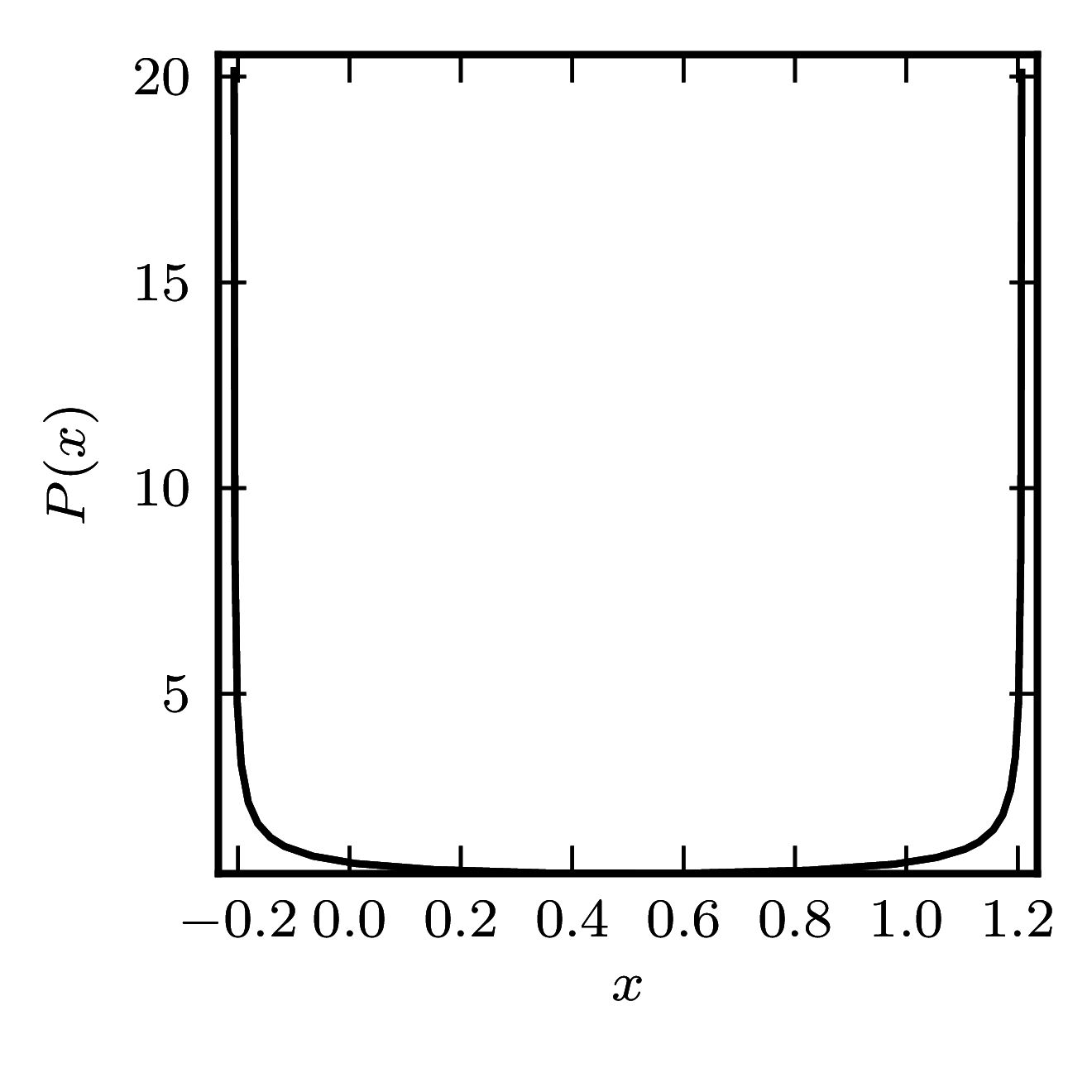 |