Normalized numerical range
Definition
The classical numerical range $F(A)$ of $A\in M_n(\mathbb{C})$ is by definition the set of values of the corresponding quadratic form $x^*Ax$ on the unit sphere $S^n := \{x ^n : \|x \|=1 \}$of$^n$. Equivalently, \[ F(A) =\{(x^*Ax)/||x||2 xn\{0\}\}. \] Various modifications and generalization of the numerical range have been considered in the literature. Our paper is concerned with the so called normalized numerical range. Defined as \[ F_N(A) := \{ x ^n, Ax 0 \},\] it was introduced in [1], and then further investigated in for example [2].
Properties
Suppose that $A \in M_n(\mathbb{C})$. Then:
- For all $z \in F_N(A)$, $|z| \le 1$.
*If $z \in F_N(A)$, then $|z| = 1$ if and only if $z = /||$for some$(A)$.
-
$F_N(A)$ is unitarily invariant: $F_N(U^*AU)=F_N(A)$ for any unitary $U\in M_n(\mathbb{C})$.
-
$F_N(e^{i\theta}A) = e^{i\theta} F_N(A)$ for all $ [0,2)$.
-
$F_N(cA) = F_N(A)$ for all $c > 0$.
-
If $A$ is invertible, then $F_N(A)$ is closed.
The following theorems and examples are taken from [3].
Theorem 1
Suppose that $A \in M_2(\mathbb{C})$ has non-zero eigenvalues $\lambda_1, \lambda_2$ such that $\lambda_1/\lambda_2 < 0$. Then $F_N(A)$ is a closed elliptical disk. In the case when $A > 0$, the ellipse is given by the equation
Theorem 2
For $A \in M_2 (\mathbb{C}) \backslash \{0\}$ with eigenvalues $\lambda_1$ and $\lambda_2$, the boundary of $F_N(A)$ is an ellipse if and only if $|\lambda_1| = |\lambda_2|$ or $\lambda_1/\lambda_2 < 0$.
Examples
1. The normalized numerical range of $A =
$.
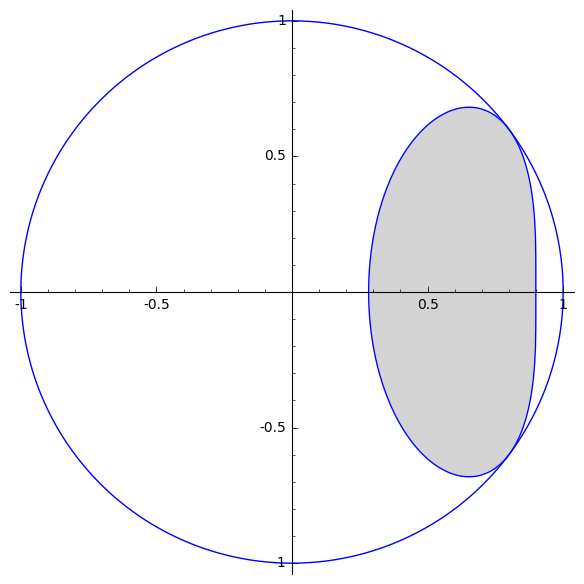
2. The normalized numerical range of $B =
$.

3. The normalized numerical range of $C =
$.
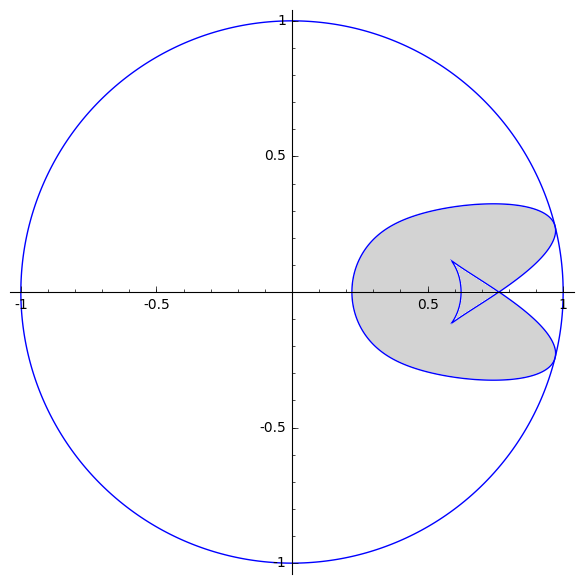
For matrix $A$ is a typical example of convex normalized numerical range that is not an ellipse. The normalized numerical range of matrix $B$ is not convex, but has a smooth boundary (boundary is differentiable). Finally, the last example for matrix $C$ has a boundary that is not smooth at one point. All three of these examples have boundaries that satisfy irreducible 8th degree polynomial equations.
References
- [1]W. Auzinger, “Sectorial operators and normalized numerical range,” Applied numerical mathematics, vol. 45, no. 4, pp. 367–388, 2003, [Online]. Available at: https://www.sciencedirect.com/science/article/pii/S0168927402002544.
- [2]L. Z. Gevorgyan, “Normalized numerical ranges of some operators,” Operators and Matrices, vol. 3, no. 1, pp. 145–153, 2009, [Online]. Available at: https://nyuscholars.nyu.edu/en/publications/on-the-normalized-numerical-range.
- [3]B. Lins, I. M. Spitkovsky, and S. Zhong, “The normalized numerical range and the Davis–Wielandt shell,” Linear Algebra and its Applications, vol. 546, pp. 187–209, 2018, [Online]. Available at: https://www.sciencedirect.com/science/article/pii/S0024379518300417.