Example 1
A generic matrix $M=\begin{pmatrix} 1 & 1 & 1 & 1\ 0 & \ii & 1 & 1\ 0 & 0 & -1 & 1\ 0 & 0 & 0 & \ii \end{pmatrix}$ has an oval–like numerical range $W (M)$.
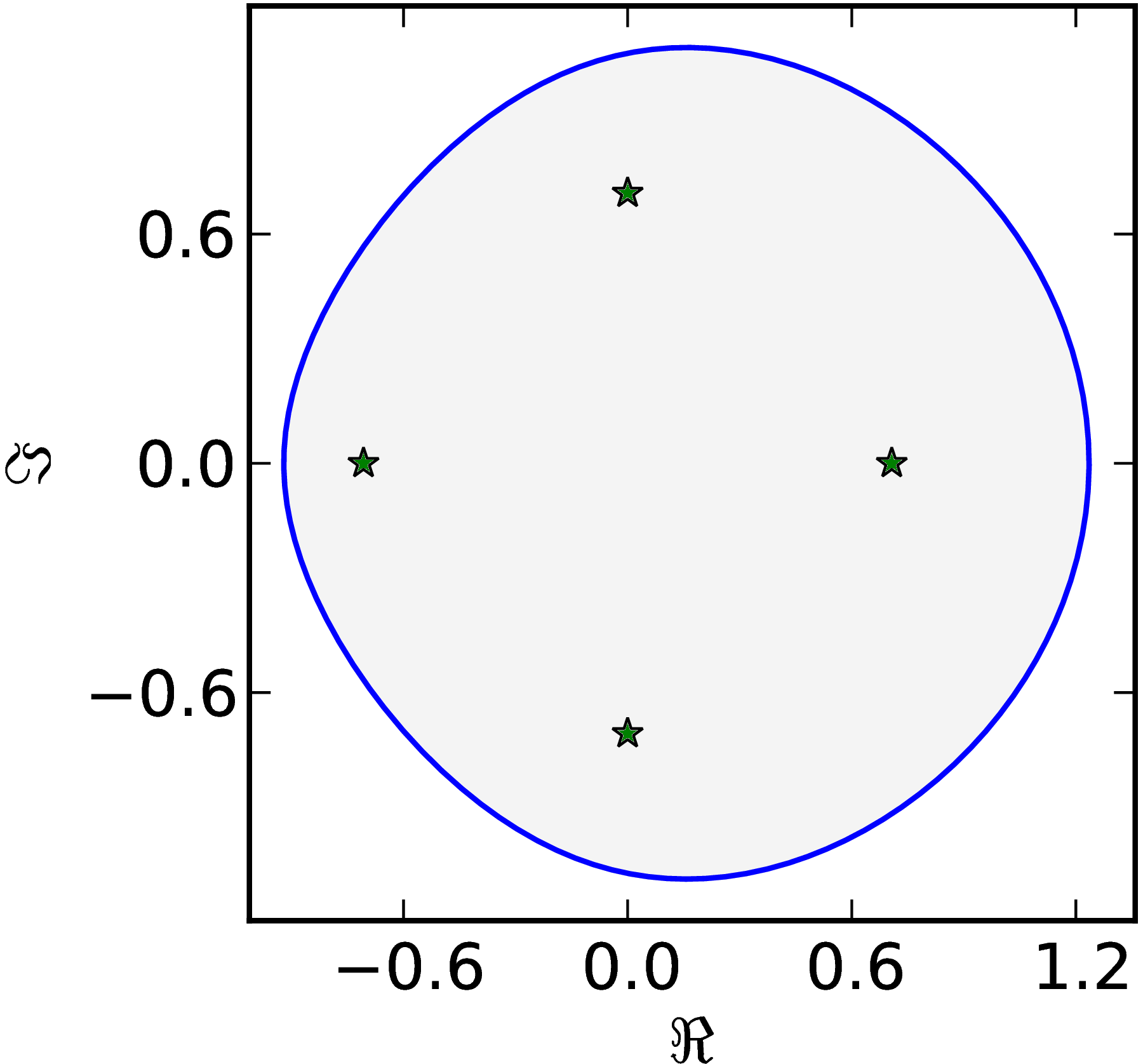 |
Example 2
The matrix $M=\begin{pmatrix} 1 & 1 & 1 & 1\ 0 & \ii & 1 & 1\ 0 & 0 & -1 & 1\ 0 & 0 & 0 & \ii \end{pmatrix}$ has a numerical range $W (M)$ with one flat part of the boundary $\partial W$.
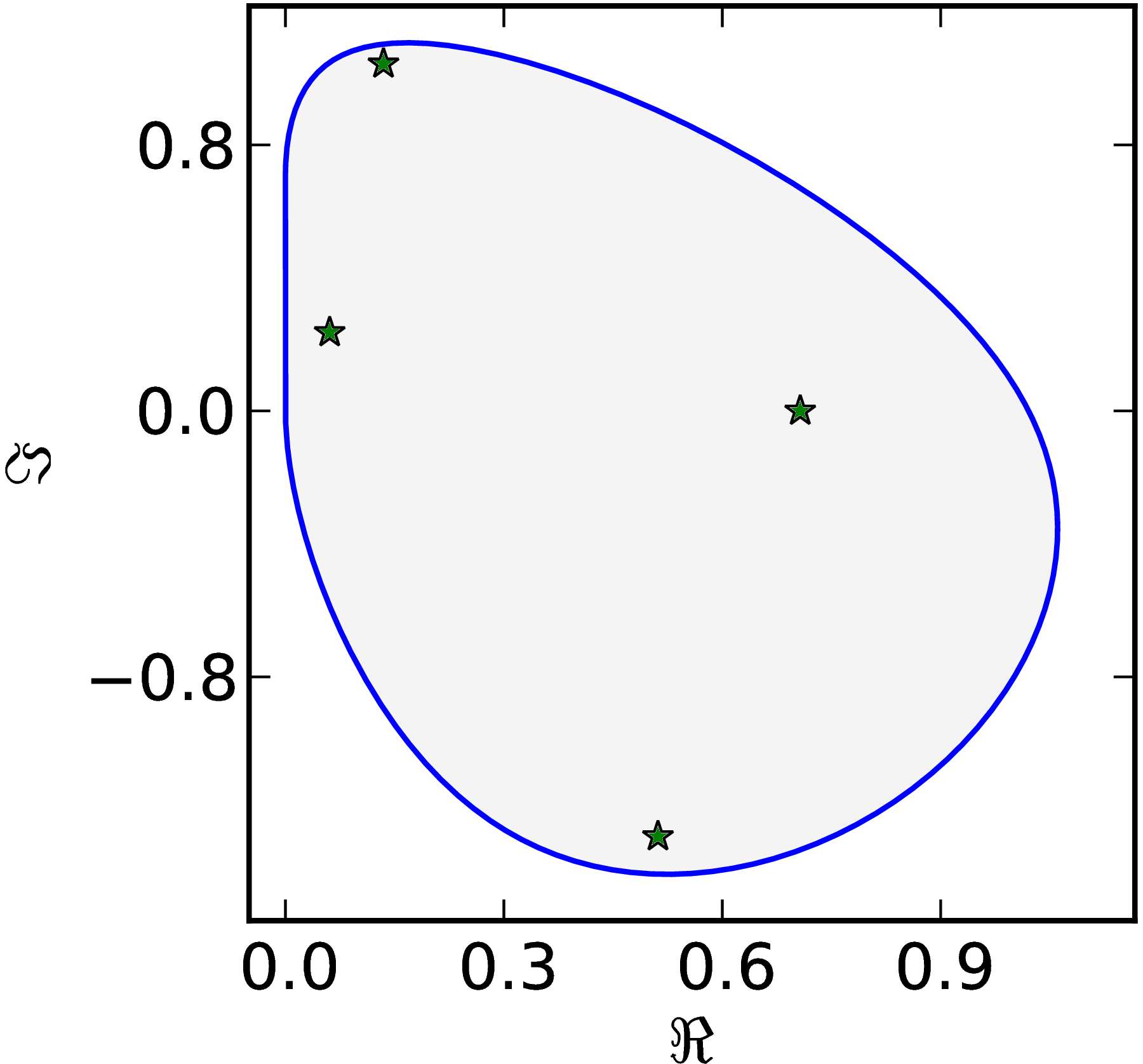 |
Example 3
The matrix $M=\begin{pmatrix} 1 & 0 & 0 & 1\ 0 & \ii & 0 & 1\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & 1 \end{pmatrix}$ has a numerical range $W (M)$ with two flat parts of of the boundary $\partial W$.
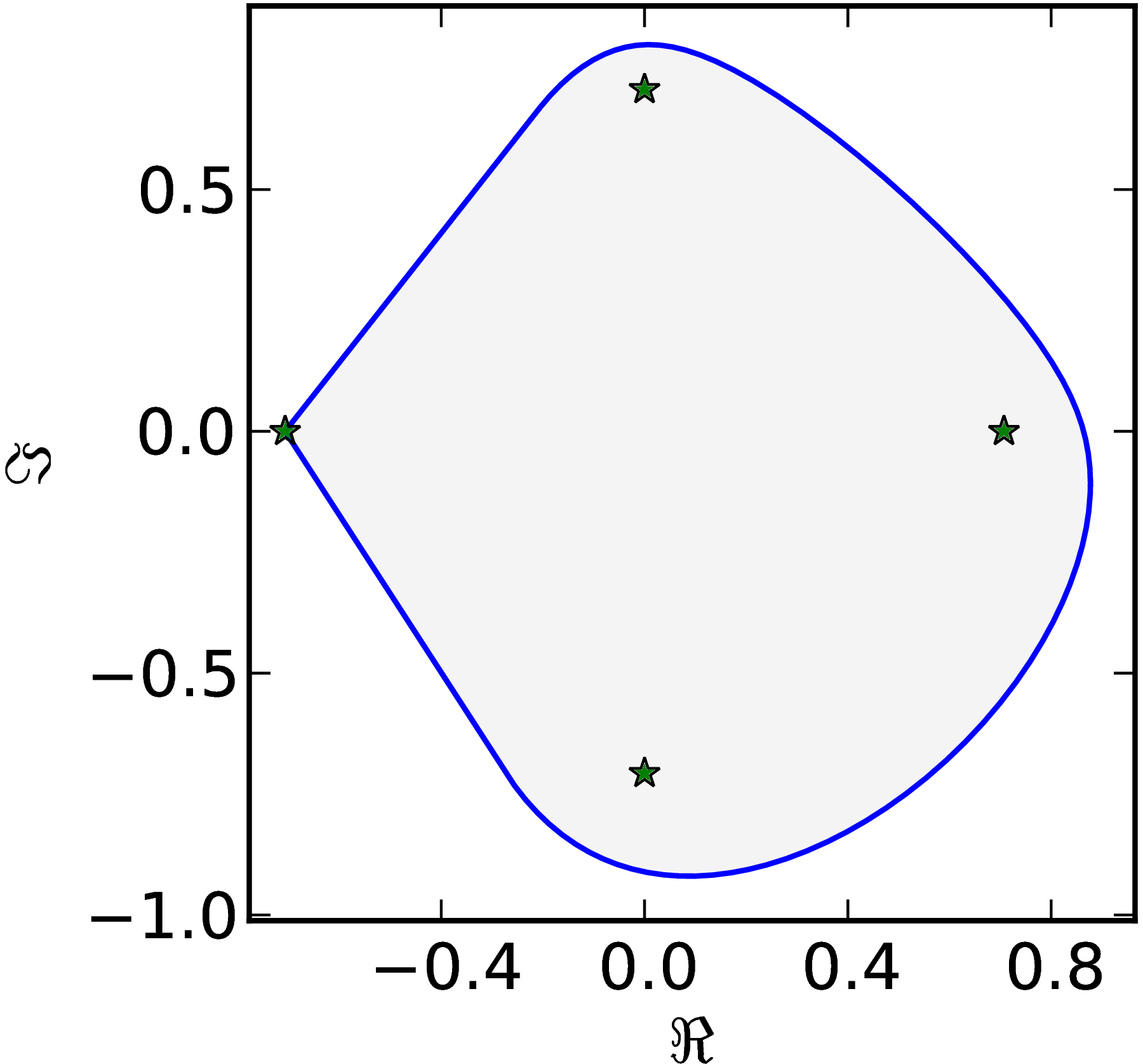 |
Example 4
The matrix $M=\begin{pmatrix} 1 & 0 & 0 & 1\ 0 & \ii & 1 & 0\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & -\ii \end{pmatrix}$ has a numerical range $W (M)$ with two parallel flat parts of of the boundary $\partial W$.
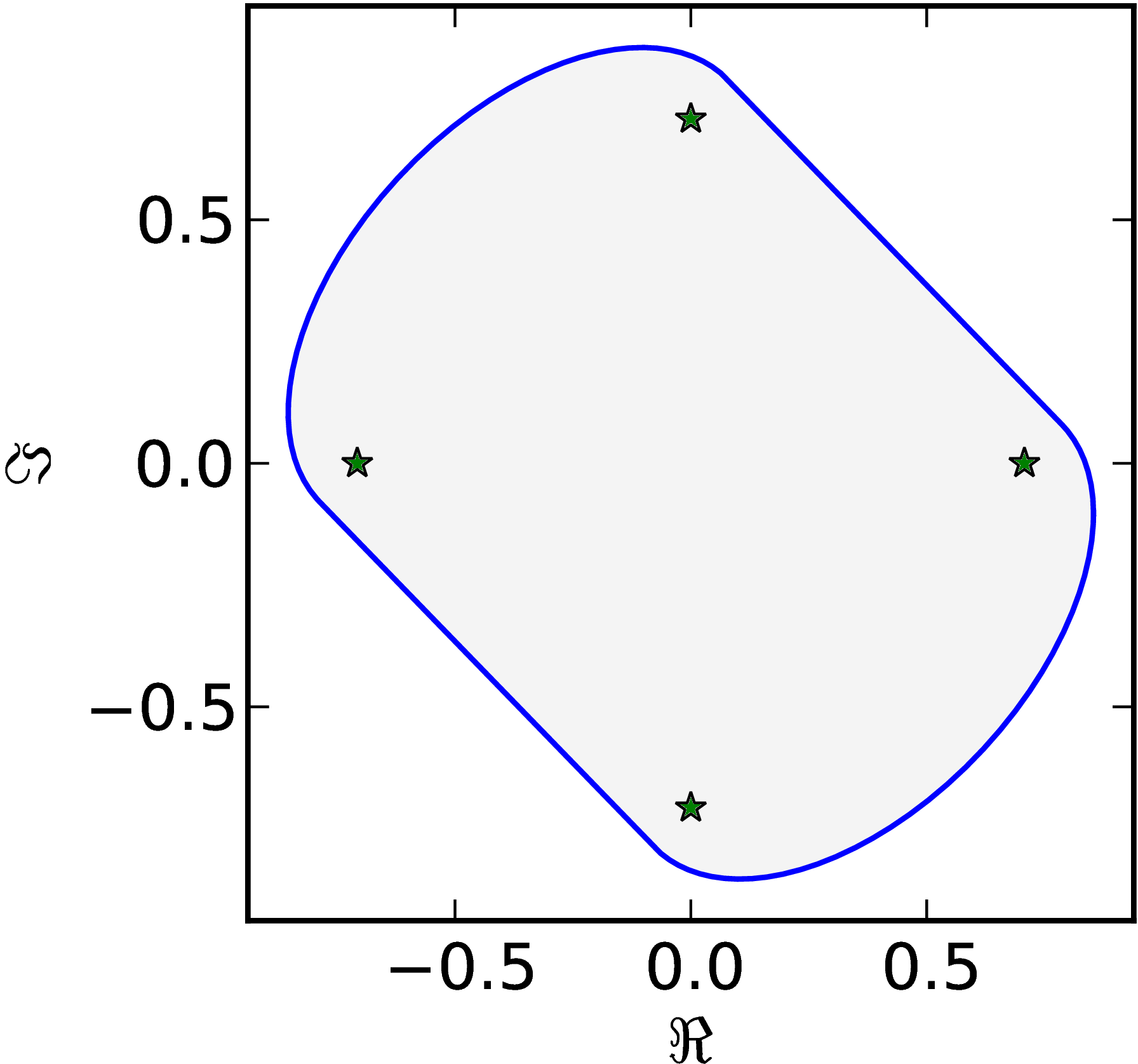 |
Example 5
The matrix $M=\begin{pmatrix} 1 & 0 & 0 & 1\ 0 & \ii & 0 & 0\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & -\ii \end{pmatrix}$ has a numerical range $W (M)$ with three flat parts of $\partial W$ connected with corners and one oval–like part.
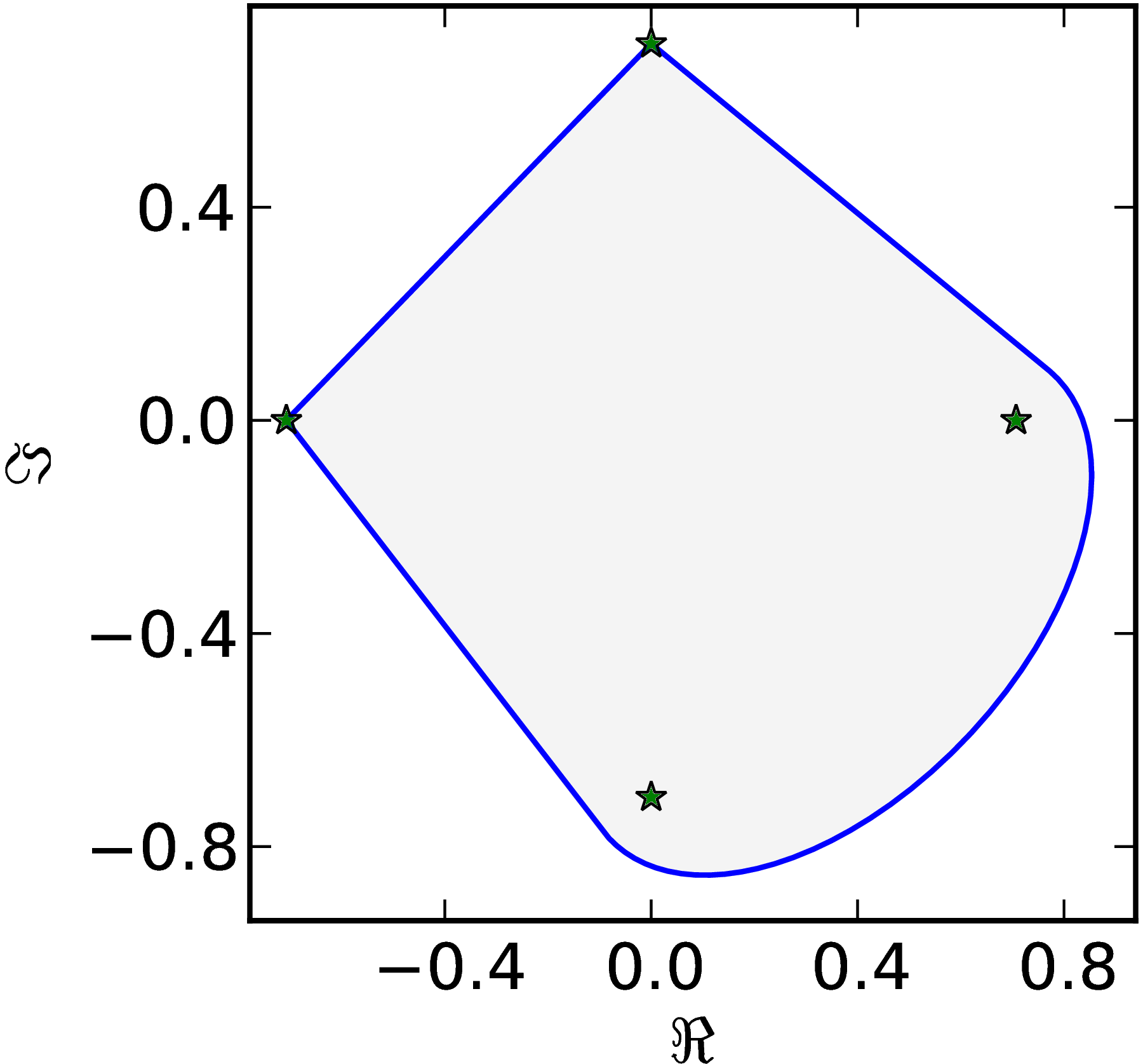 |
Example 6
The matrix $M=\begin{pmatrix} \ii & 0 & -1 & 0\ 0 & 0 & -1 & 0\ 1 & 1 & 1-\ii & 0\ 0 & 0 & 0 & 1 \end{pmatrix}$ has a numerical range $W (M)$ with three flat parts of $\partial W$ with only one corner and two oval–like parts.
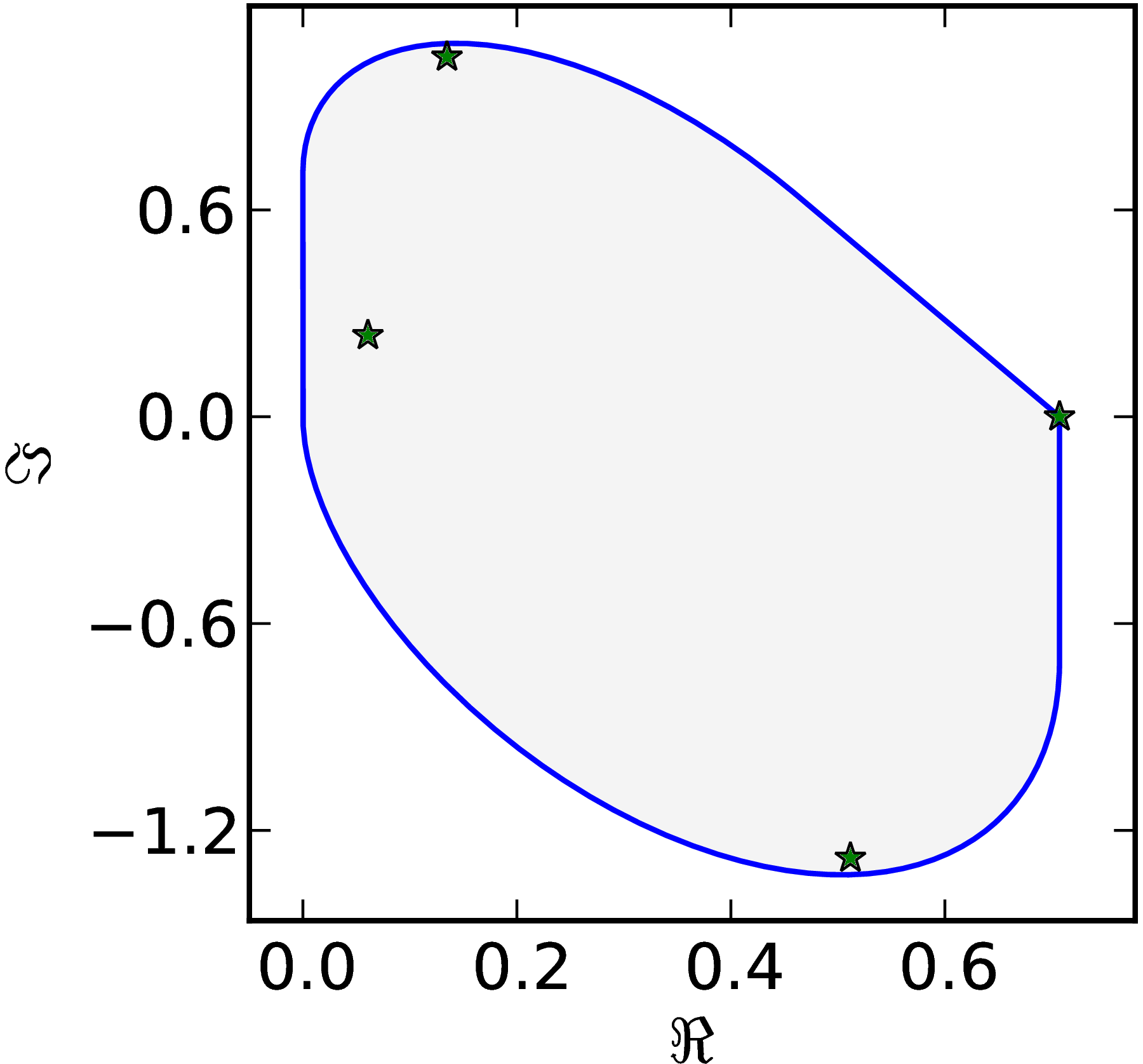 |
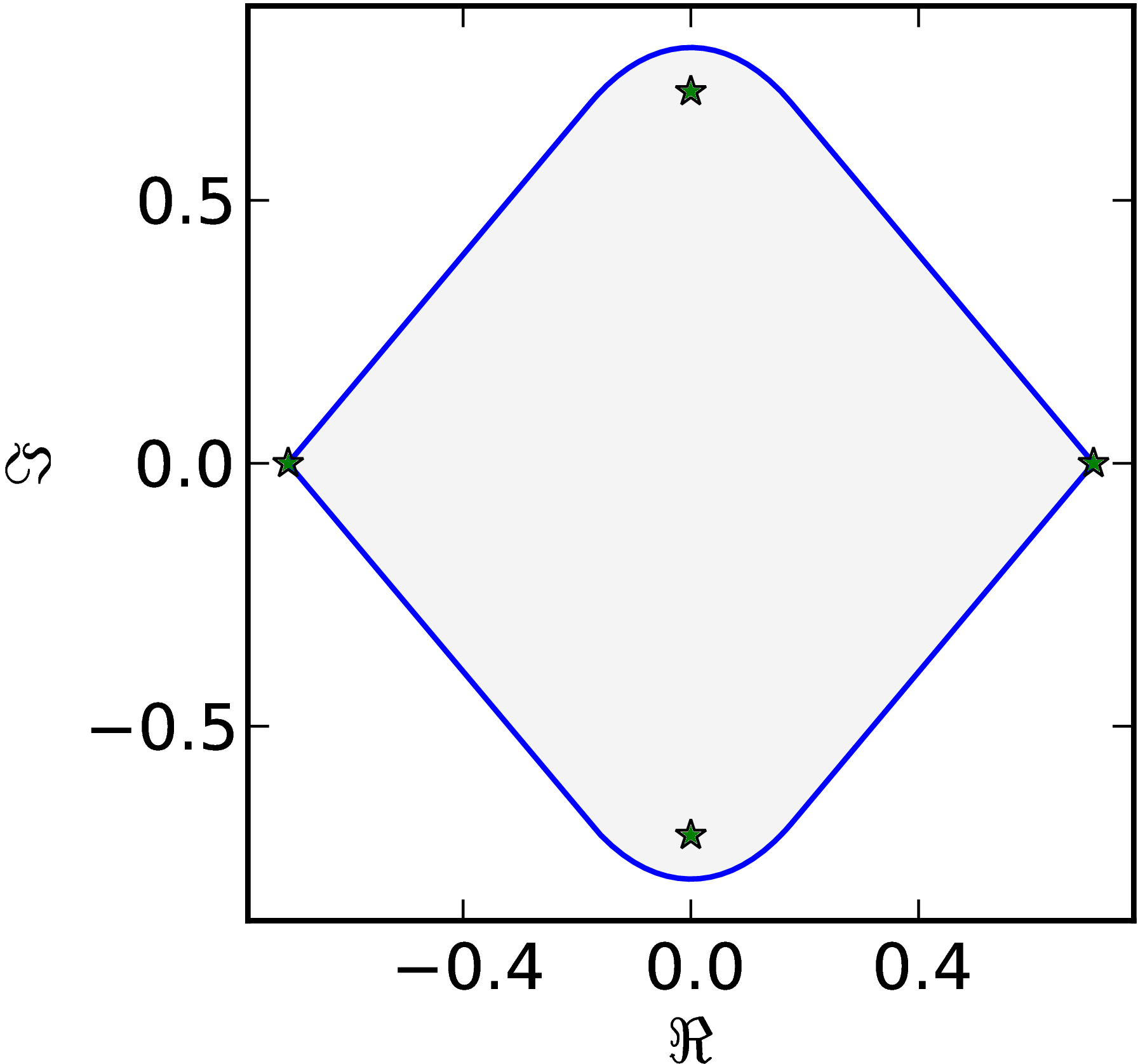
Example 7
The matrix $M=\begin{pmatrix} 1 & 0 & 1 & 0\ 0 & \ii & 0 & 1\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & -\ii \end{pmatrix}$ has a numerical range $W (M)$ with four flat parts of $\partial W$.
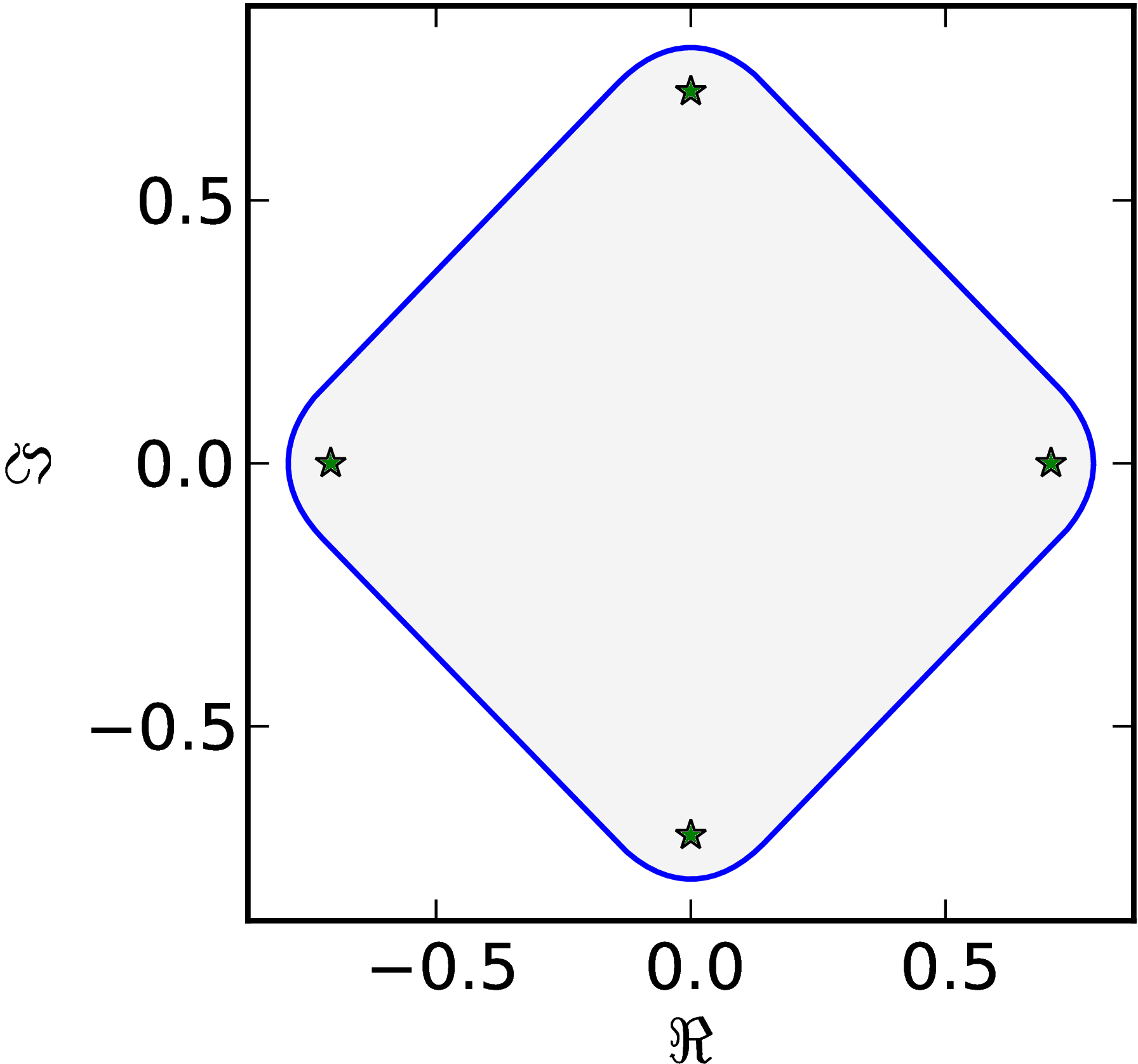 |
Example 8
The matrix $M=\begin{pmatrix} 1 & 0 & 0 & 0\ 0 & \ii & 0 & 1\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & -\ii \end{pmatrix}$ has a numerical range $W (M)$ pair of flat parts of $\partial W$ connected with a corner connected with two oval–like parts.
 |
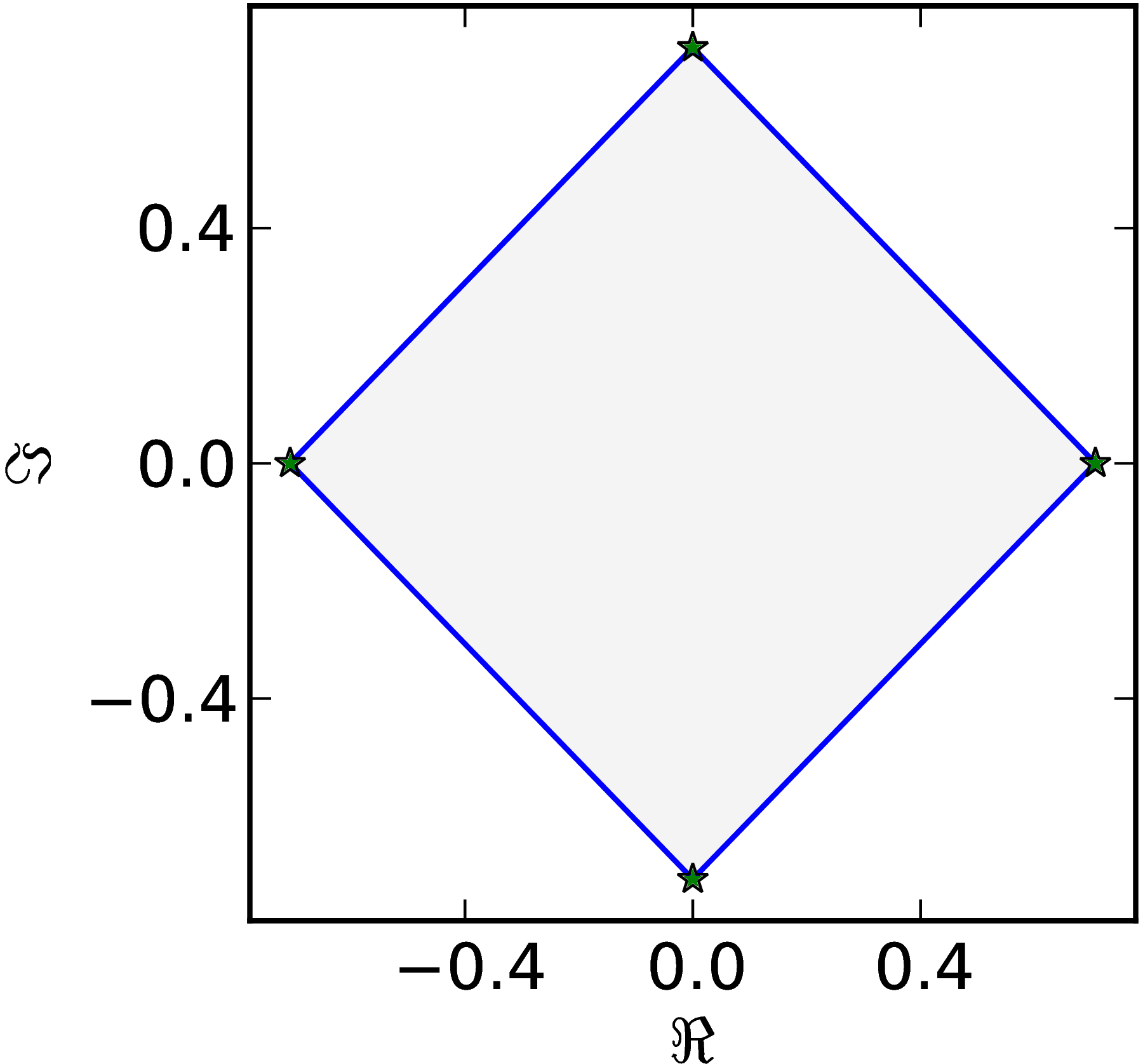
Example 9
The matrix $M=\begin{pmatrix} 1 & 0 & 0 & 0\ 0 & \ii & 0 & 0\ 0 & 0 & -1 & 0\ 0 & 0 & 0 & -\ii \end{pmatrix}$ has a numerical range $W (M)$ equal to the convex hull of eigenvalues.
 |