Hermitian matrices
In the case of Hermitian matrices the numerical shadow is a one dimensional distribution.
Diagonal matrices
Example 1
The matrix is $\mathrm{diag}(1, 2, 3, 4 ,5, 6)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
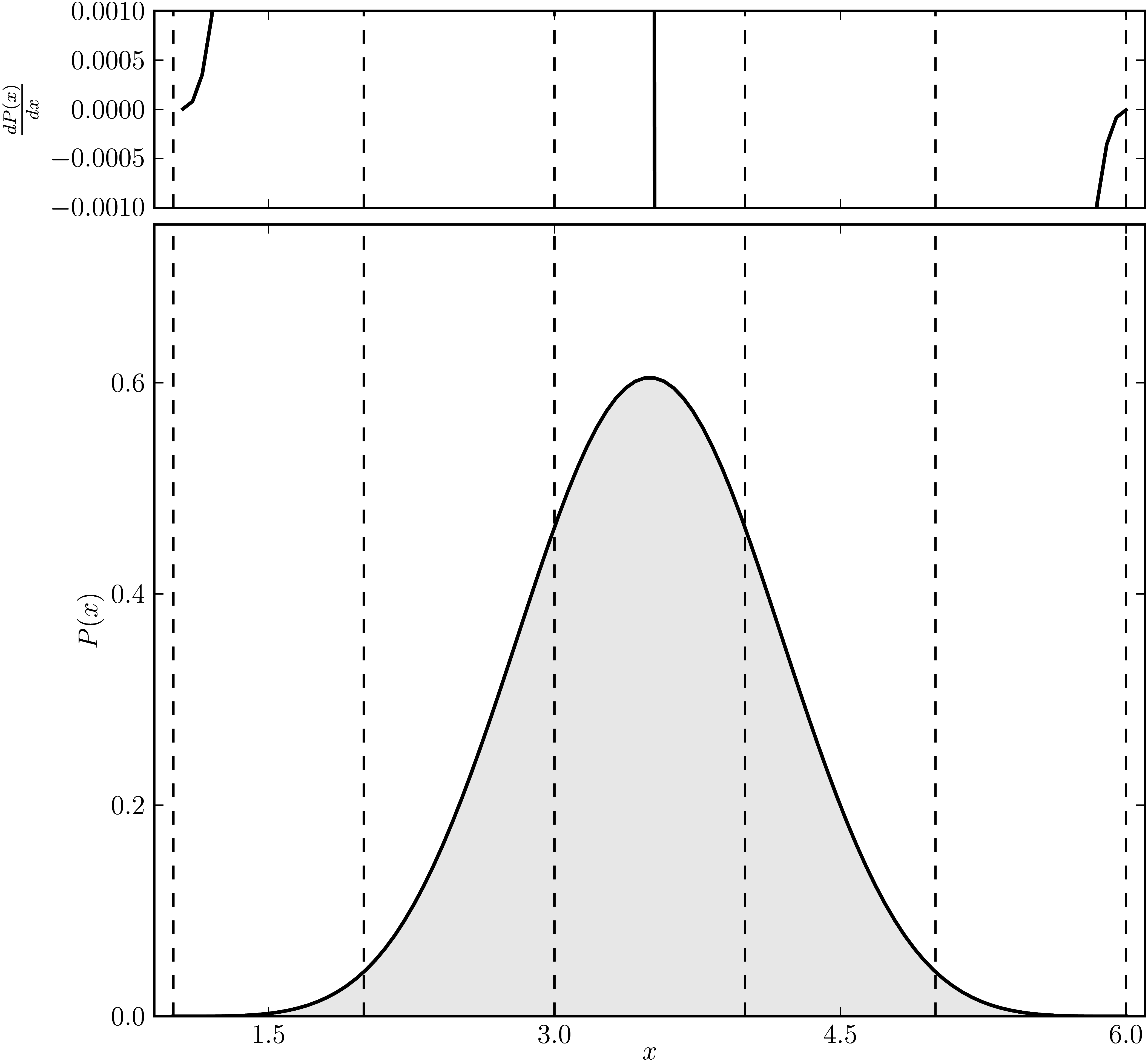 | 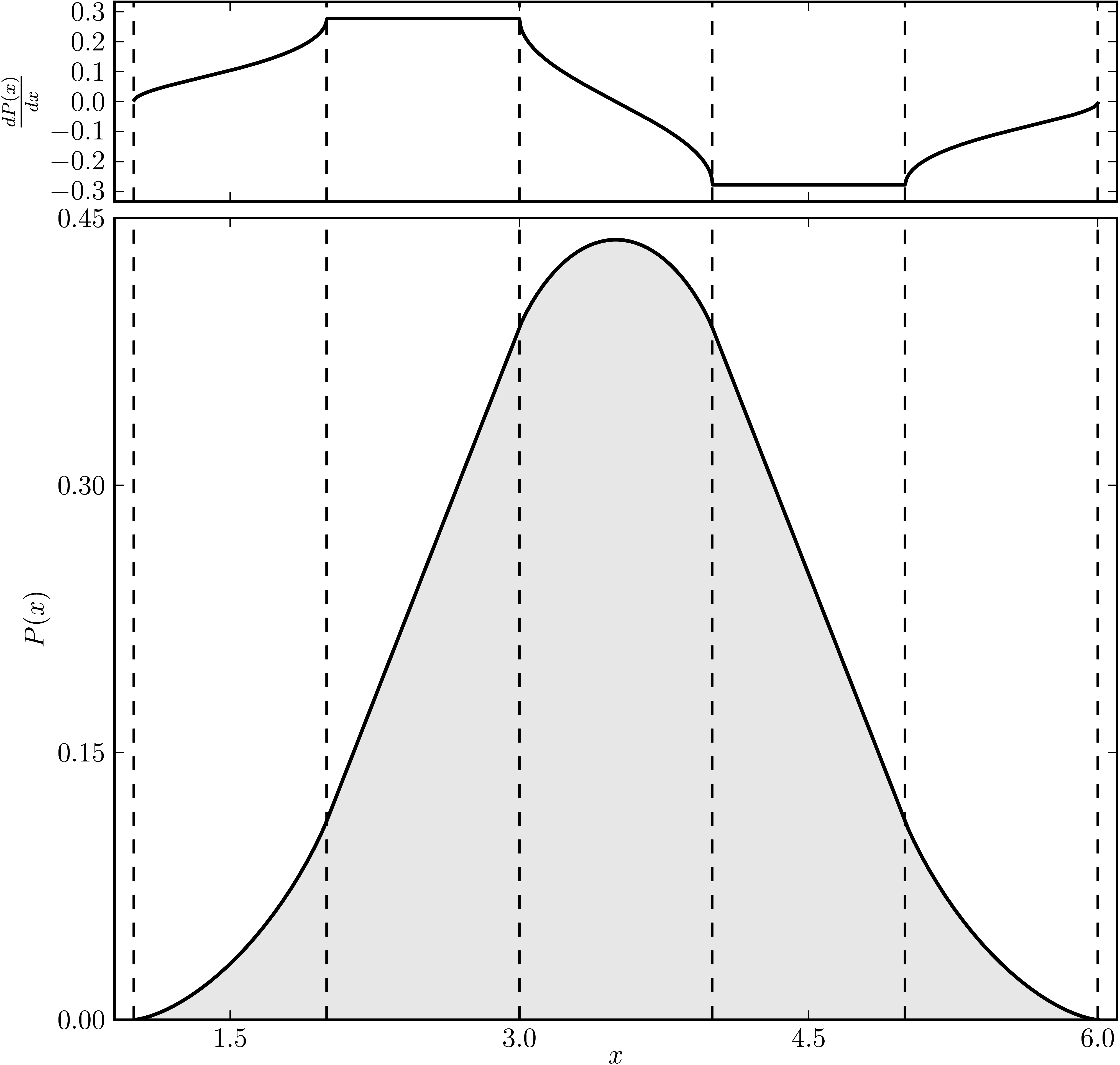 |
Example 2
The matrix is $\mathrm{diag}(1, 2, 2, 4 ,5, 6)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
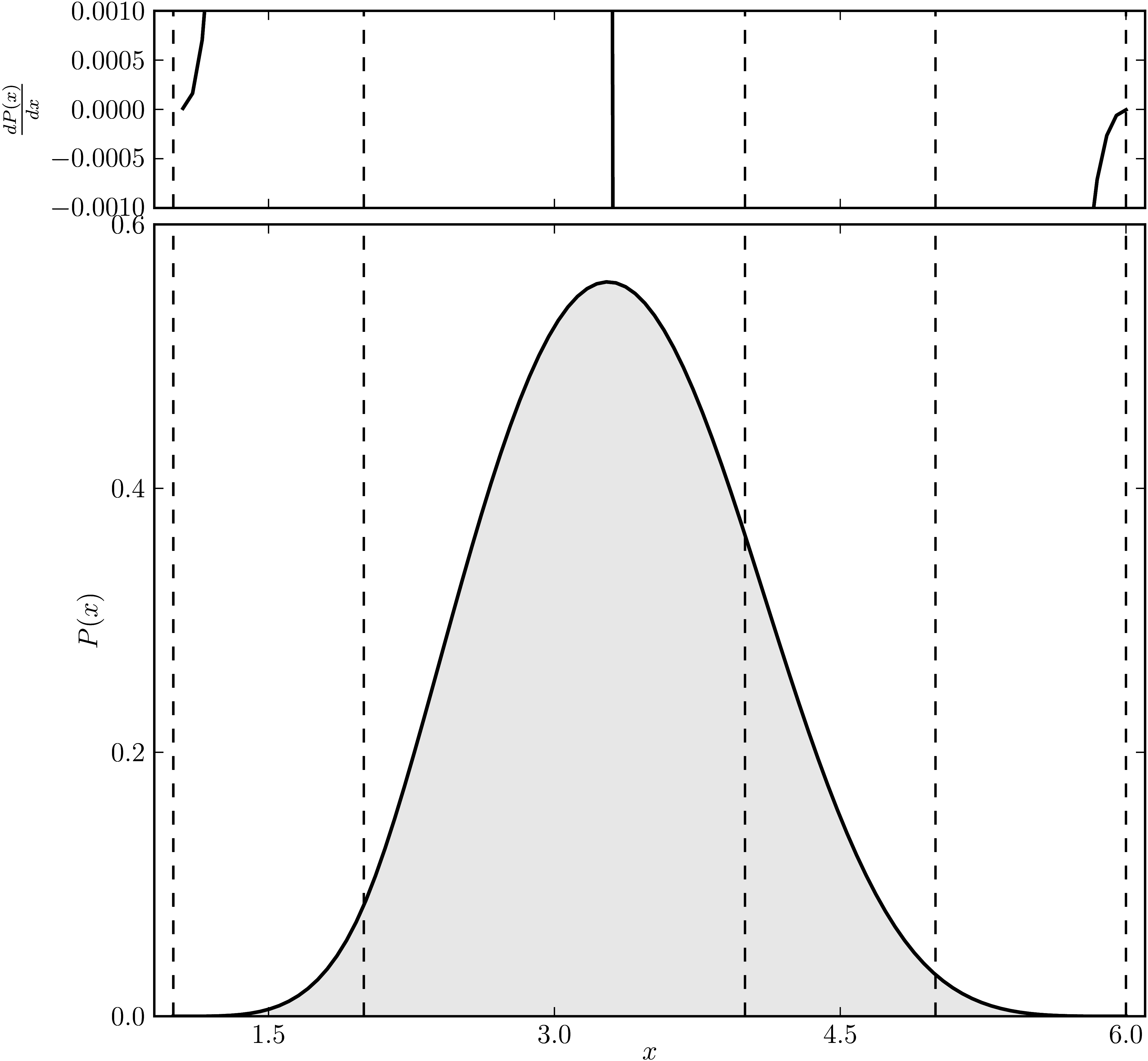 | 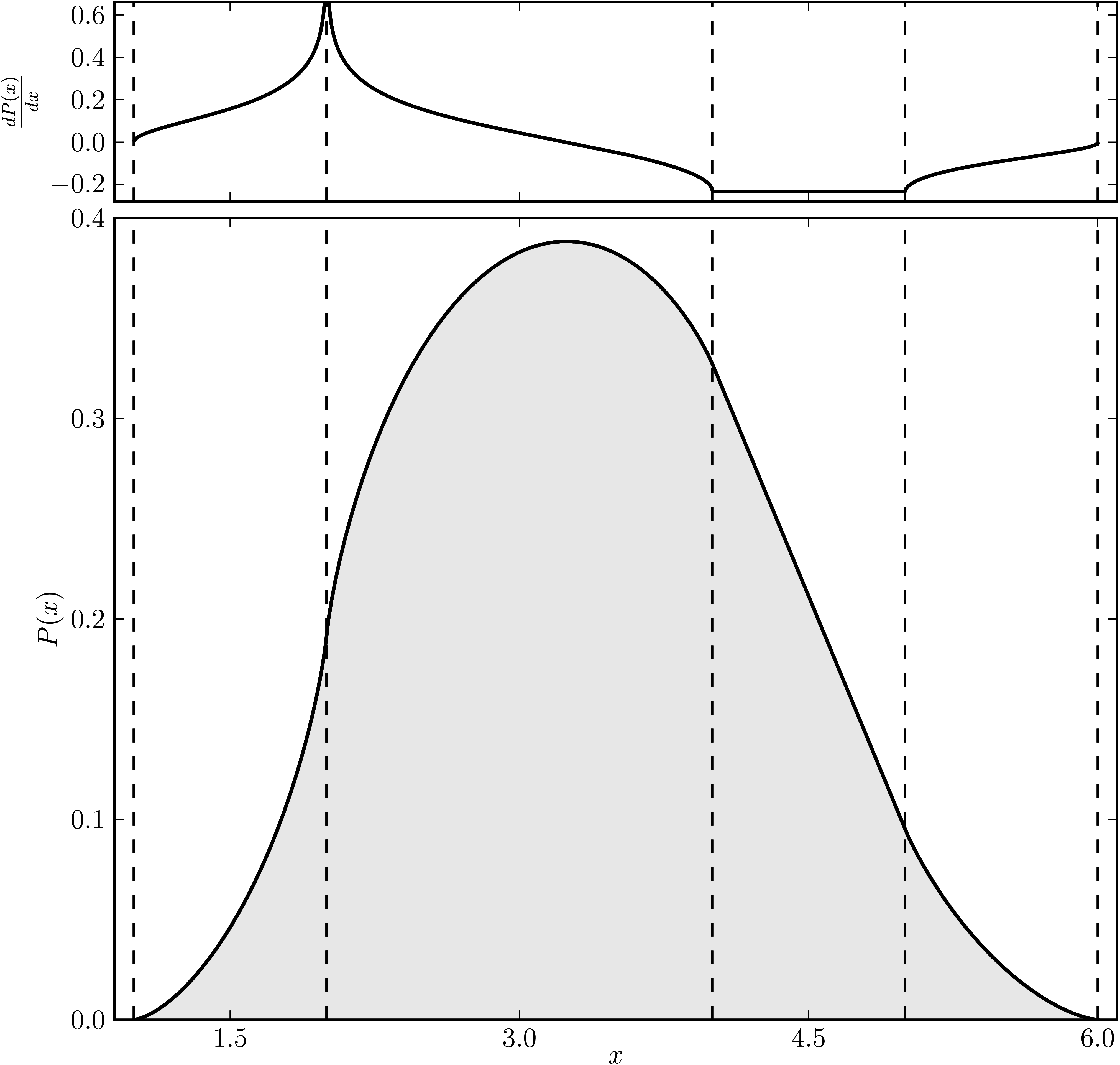 |
Example 3
The matrix is $\mathrm{diag}(1, 2, 2, 4 ,4, 6)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
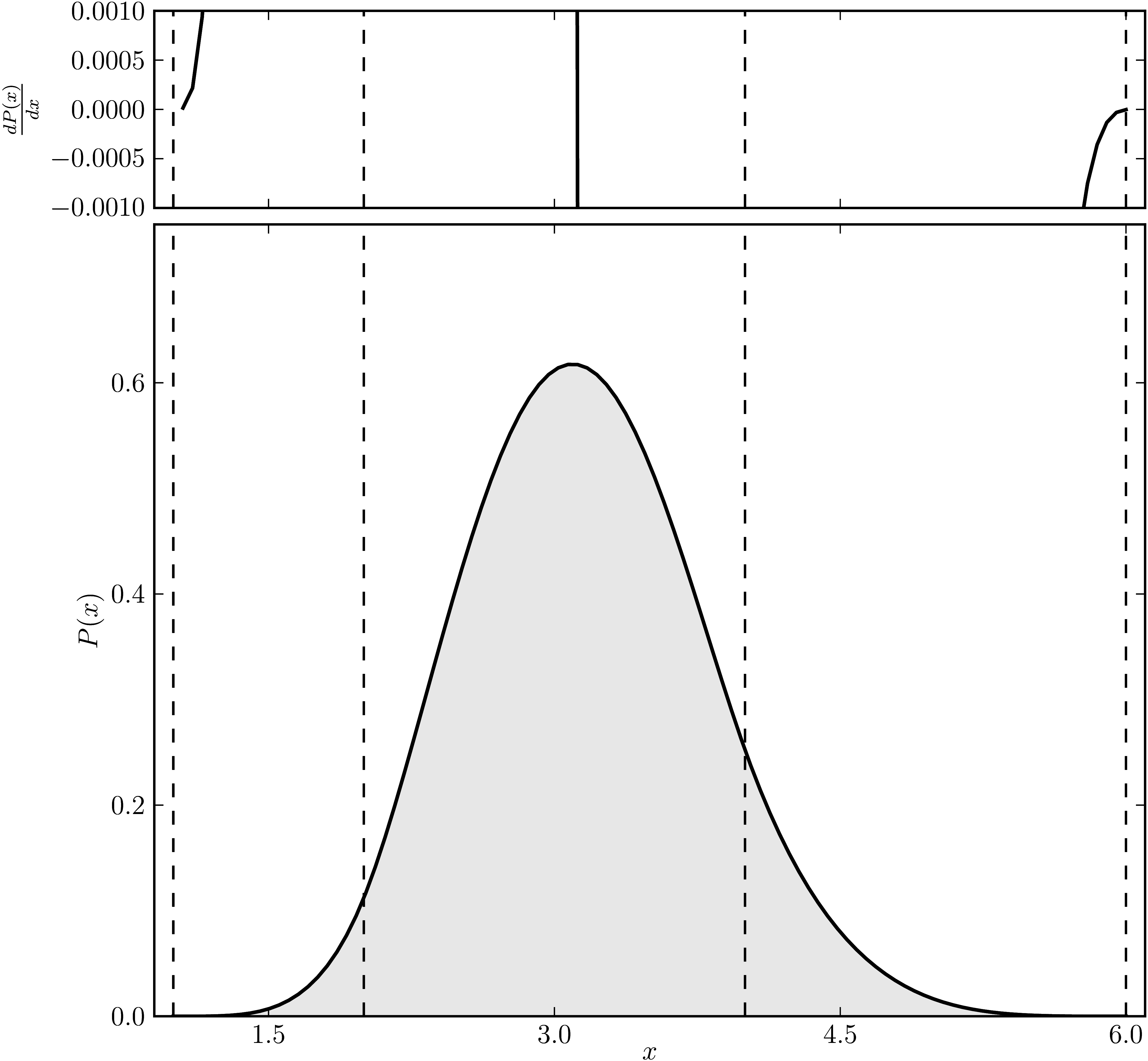 | 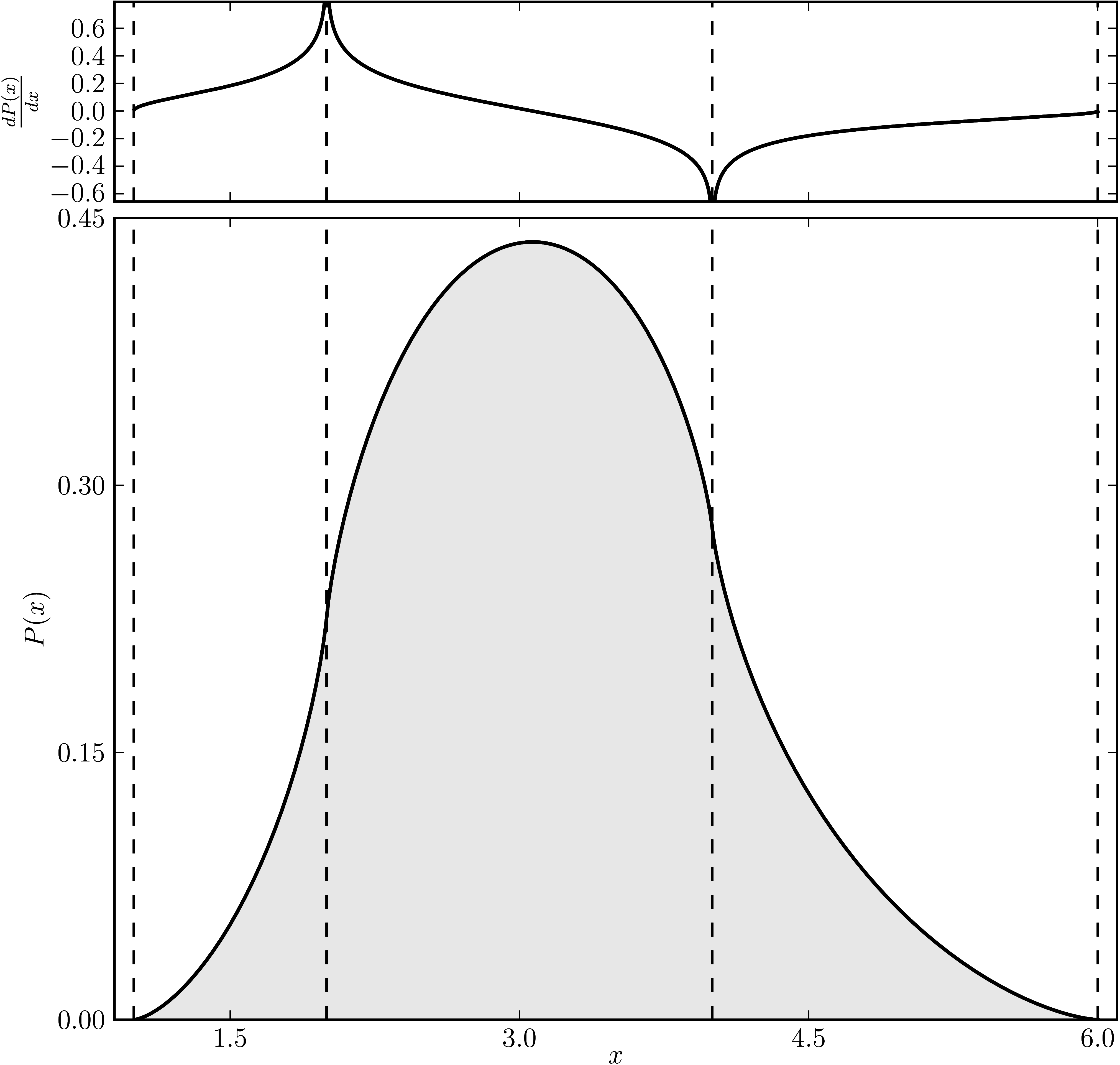 |
Example 4
The matrix is $\mathrm{diag}(1, 2, 2, 2 ,5, 6)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
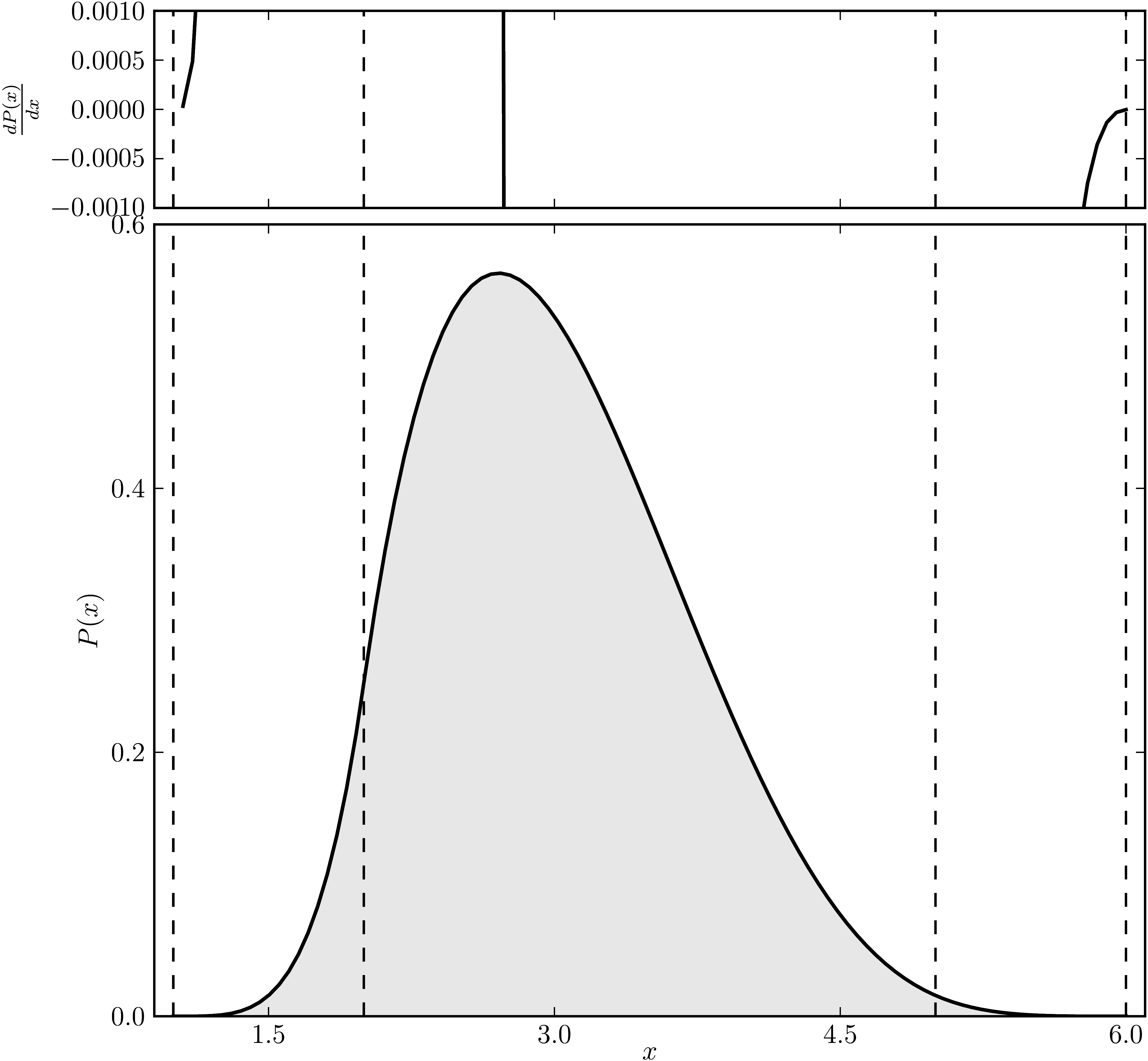 | 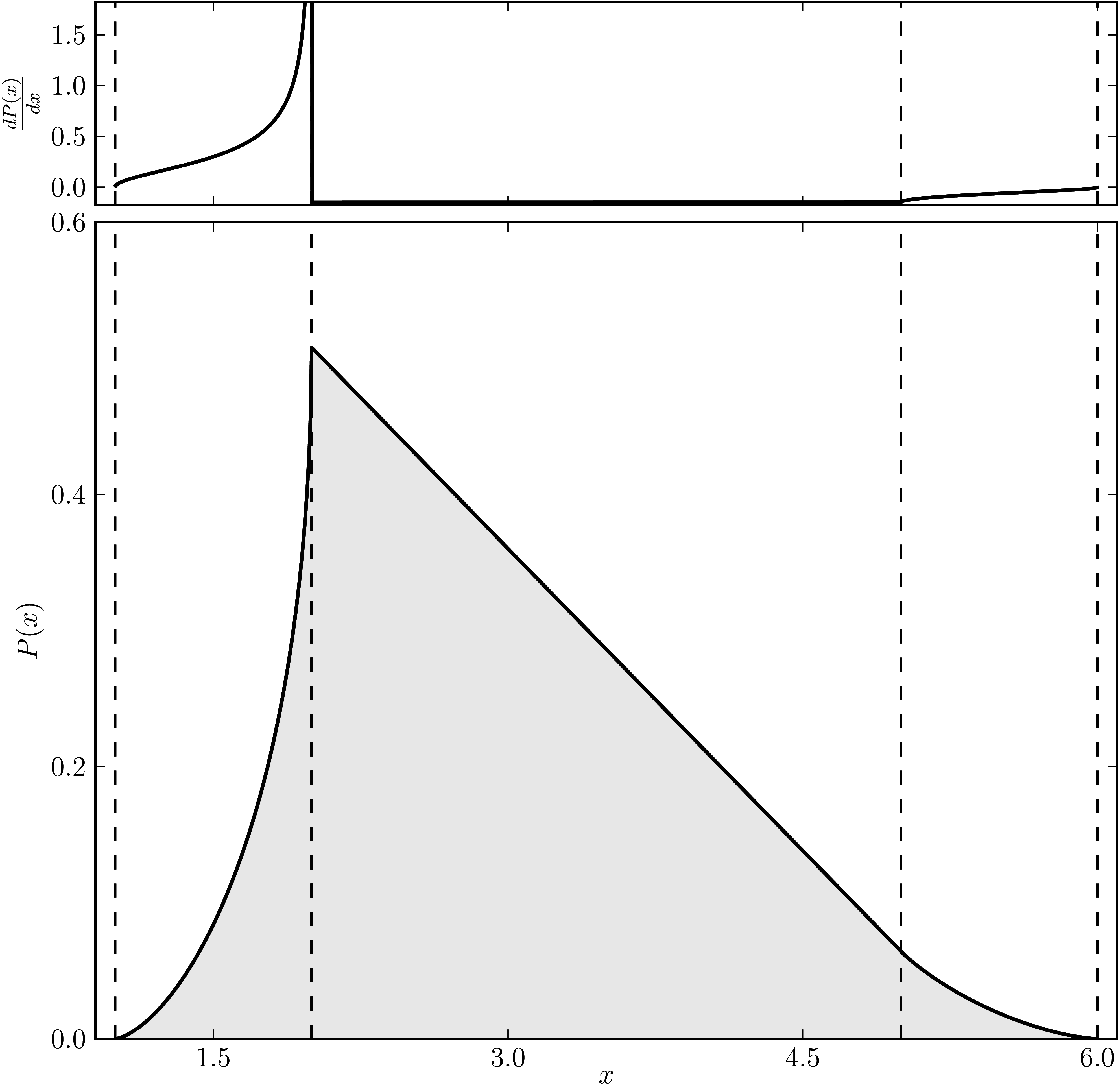 |
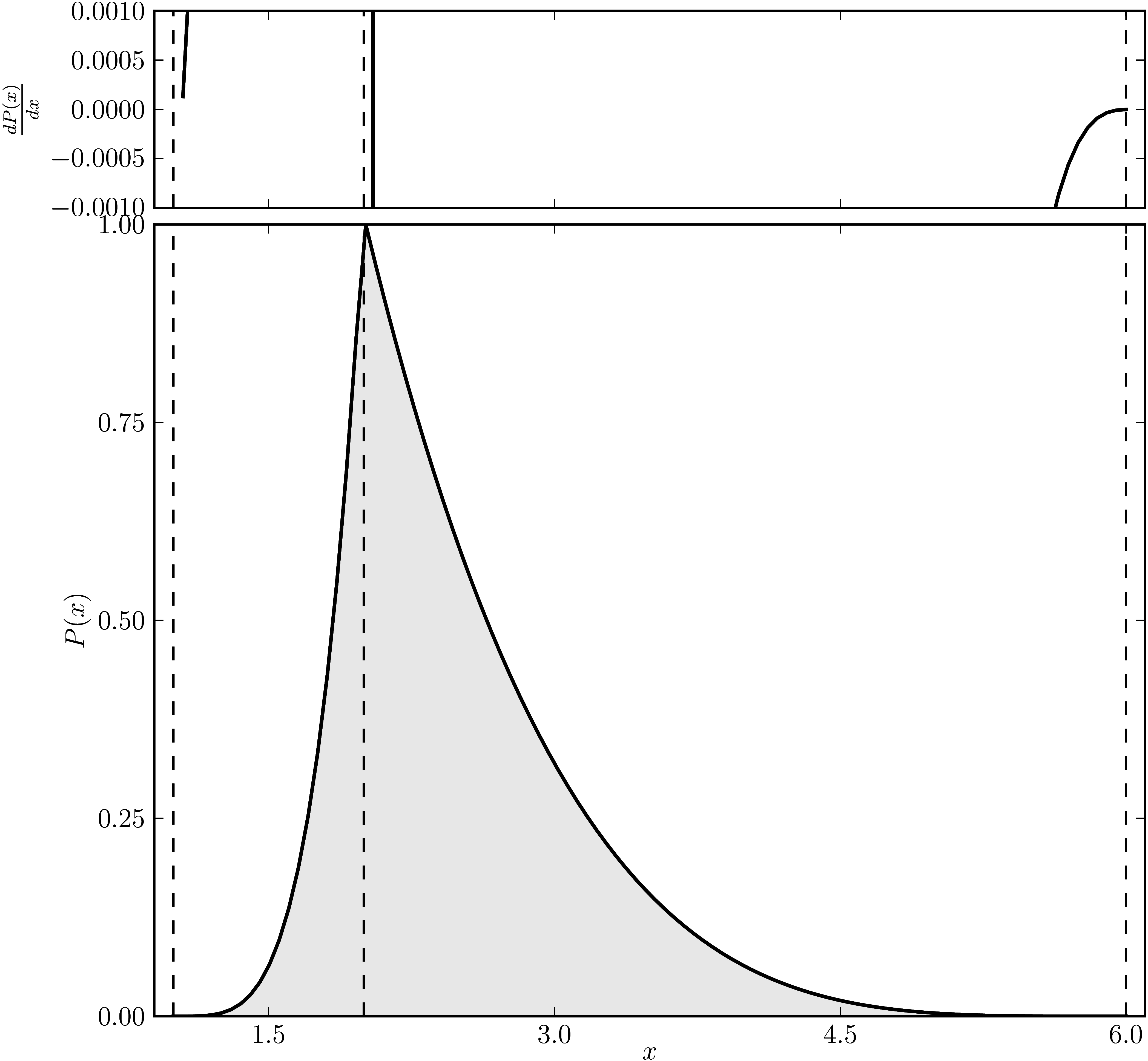
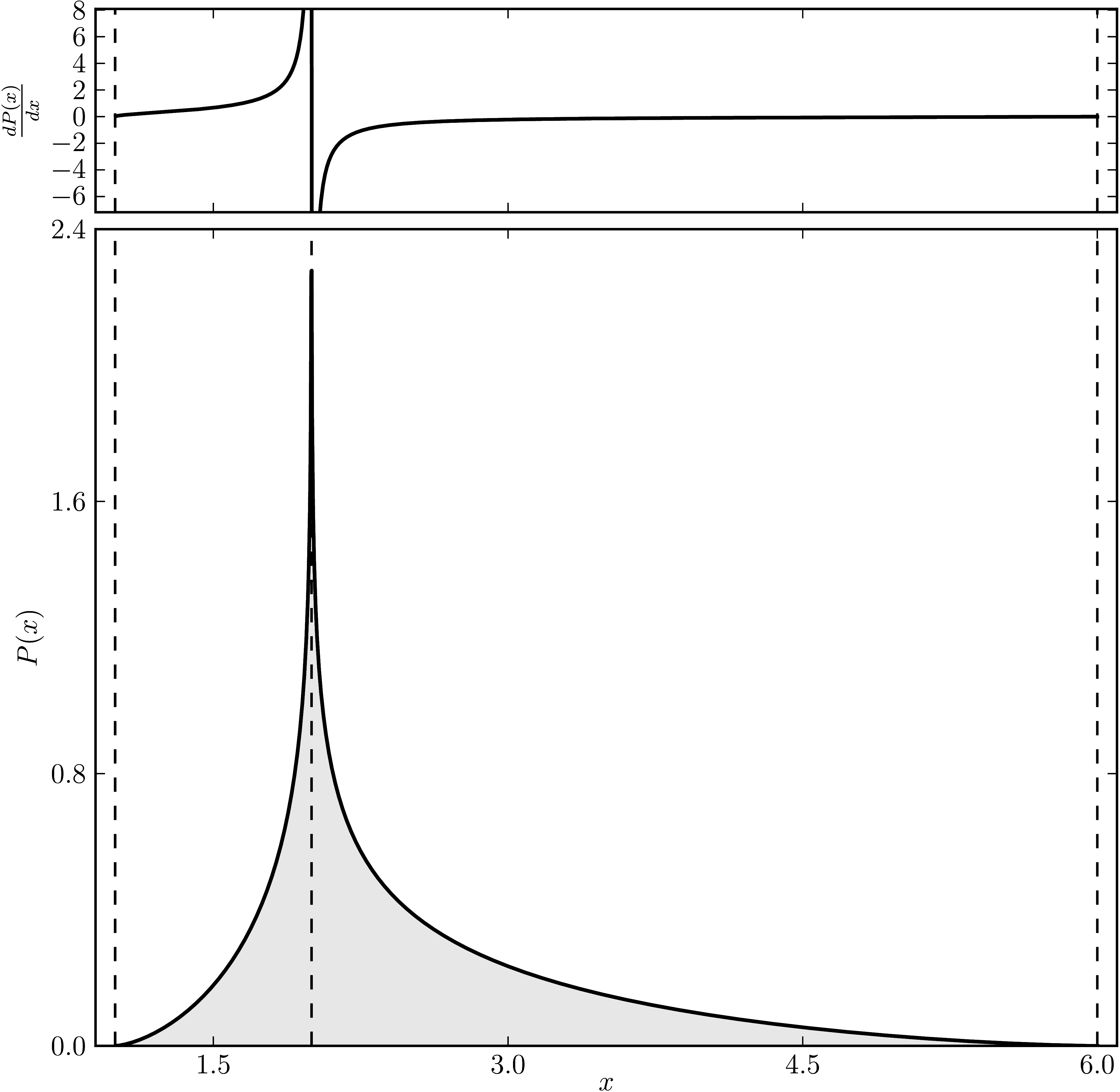
Example 5
The matrix is $\mathrm{diag}(1, 2, 2, 2 ,2, 6)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
 |  |
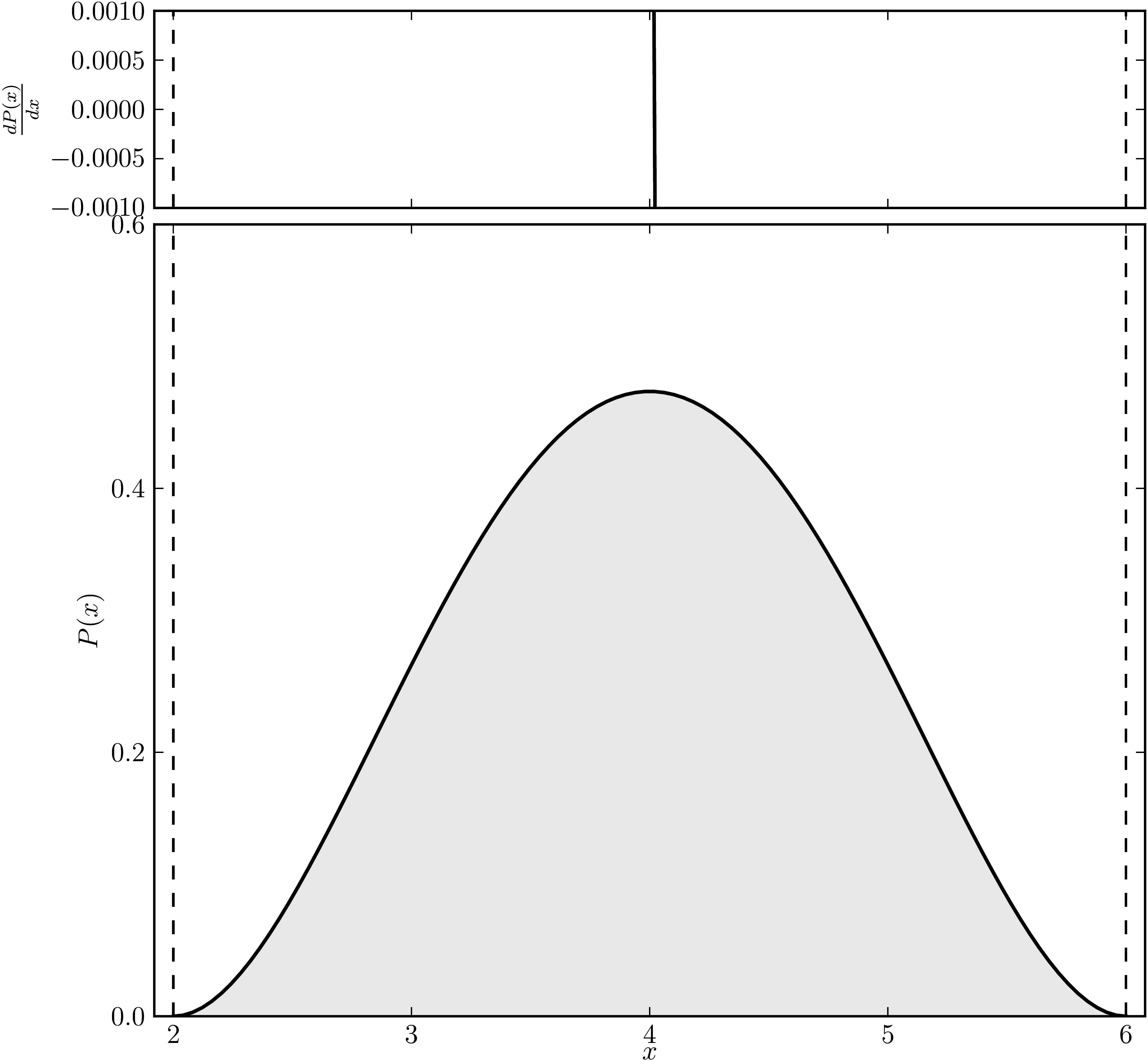
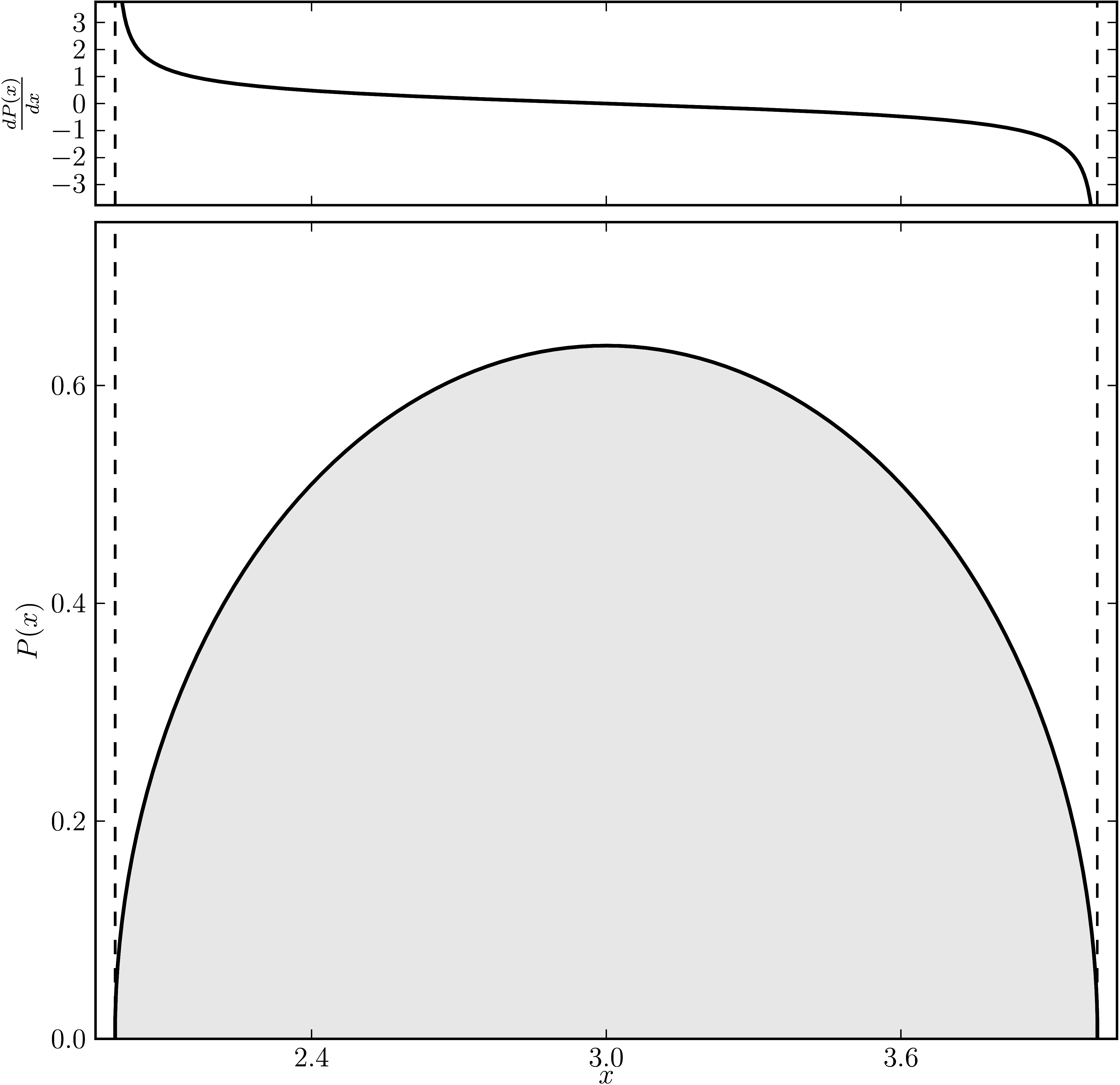
Example 6
The matrix is $\mathrm{diag}(2, 2, 2, 4 ,4, 4)$. The dashed lines mark the eigenvalues. The upped plot shows the derivative of the distribution.
| Standard numerical shadow with respect to complex states | Numerical shadow with respect to real states |
|---|---|
 |  |