Separable numerical range
Definition
Separable numerical range $W^{\mathrm{sep}}(A)$ of a square matrix $A$ of size $d = \prod_{i=1}^K d_i$ is a subset of the complex plane defined as
\[W^{\mathrm{sep}}(A)=\\{z \in \mathbb{C}:\\ z= \Tr{ \rho A,\\ \rho \in \Omega_{\mathrm{sep}} }\\},\]where $\Omega_{\mathrm{sep}}$ is a convex hull of rank one projectors on product vectors i.e. $\rho \in \Omega_{\mathrm{sep}}$ iff:
- $\rho = \sum_j p_j \ket{\psi_j}\bra{\psi_j},\$ $p_j 0 _j p_j=1$,
- $\ket{\psi_j}=\bigotimes_{i=1}^K\ket{\psi^i_j}$,
- for $i=1,\ldots,K$ and all $j$ we have $\ket{\psi^i_j}\in\mathbb{C}^{d_i}$ and $\braket{\psi^i_j}{\psi^i_j}=1$.
Fact
The separable numerical range of a matrix $A$ $W^{\mathrm{sep}}(A)$ is the convex hull of the product numerical range $W^\otimes(A)$ of this matrix $W^{\mathrm{sep}}(A) = \mathrm{conv}\left(W^\otimes(A)\right)$
Example
Consider family of unitary matrices
$U_d(\alpha_1, \alpha_2, \alpha_3)= \exp(\ii \sum_{k=1}^3 \alpha_k \sigma_k \otimes \sigma_k).$
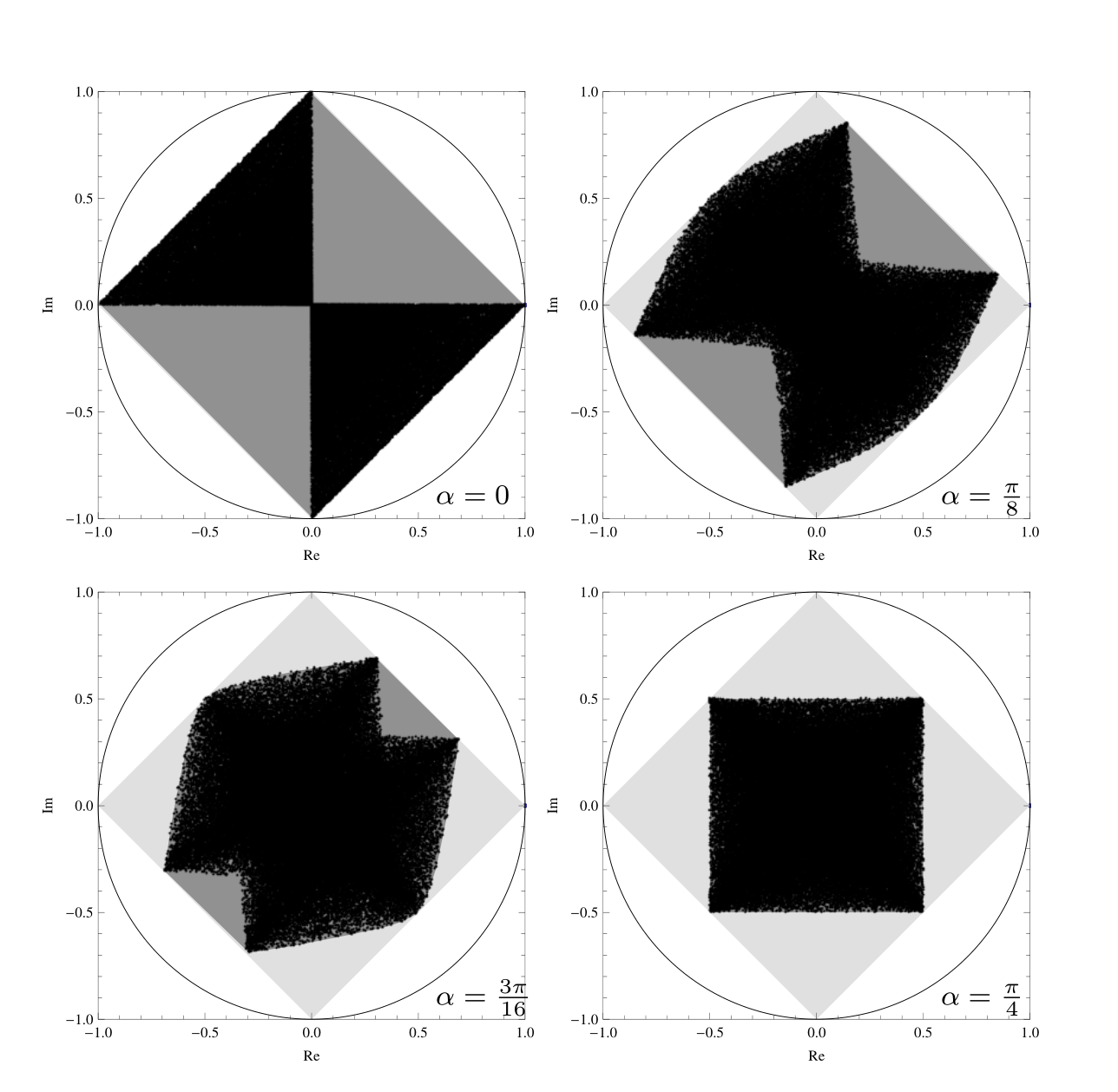
Numerical range (light gray), separable numerical range (dark gray) and product numerical range (black dots) obtained by random sampling of family of matrices $U_d(\alpha, 0, 0) (, −1, −, 1) U_d (\alpha, 0, 0)^\dagger$ for $\alpha = 0, \pi/8, 3\pi/16, \pi/4$ [1].
References
- [1]P. Gawron, Z. Puchała, J. A. Miszczak, Ł. Skowronek, and K. Życzkowski, “Restricted numerical range: a versatile tool in the theory of quantum information,” Journal of mathematical physics, vol. 51, no. 10, p. 102204, 2010, [Online]. Available at: https://aip.scitation.org/doi/abs/10.1063/1.3496901.