q-numerical range
Definition
Let $A$ be an $d \times d$ matrix. The q-numerical range of $A$ is the set: \[ W_q(A) = \{ z : z = A, = q, ^d, ^d, = 1, = 1 \}. \]
Properties
Properties of $W_q(A)$ of a matrix $A$ of dimension $d \times d$ [1], [2],[3]:
- Note that in the case $q=1$ we get back the standard numerical range;
- $W_q(A)$ is a convex and bounded set (Tsing theorem) [4];
- Unitarly invariant: $W_q(A) = W_q(UAU^\dagger)$ for any $U$ unitary matrix;
- Transpose invariant: $W_q(A) = W_q(A^\top)$;
- $ W_{qz} A) = zW_q(A)$ for any $ z \in \mathbb{C} $, such that $|z|=1$;
- For any $\mu, \eta \in \mathbb{C}$, we have $W_q(\mu A + \eta \1) = \mu W_q(A) + \eta q$.
Example
The numerical aproximation of $W_{13/14}(A)$, where $A = \begin{pmatrix} 0&1&1/2\ 0&0&1\ 0&0&0 \end{pmatrix}.$
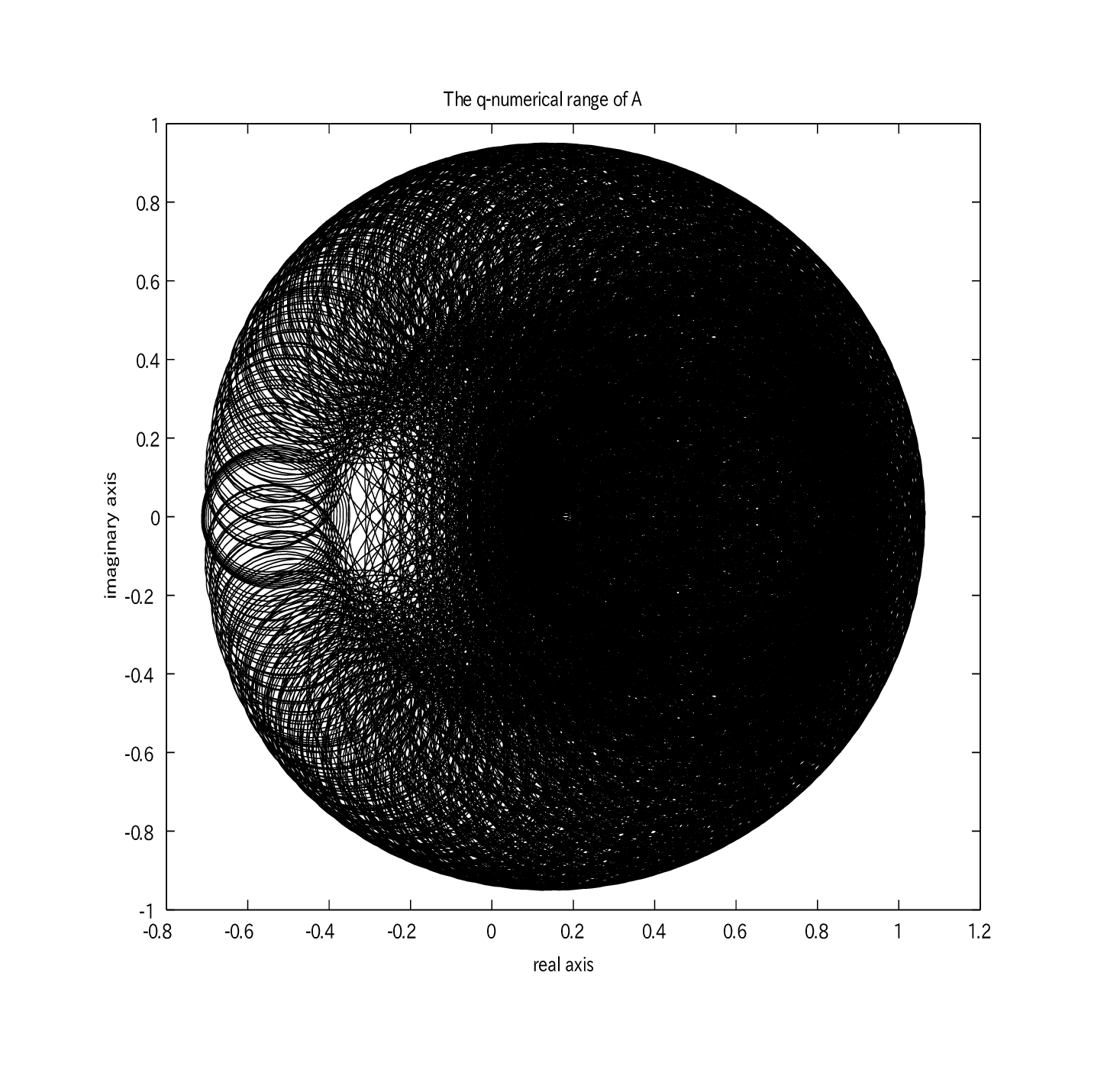
This example can be found in [5].
References
- [1]C.-K. Li, “q-Numerical ranges of normal and convex matrices,” Linear and Multilinear Algebra, vol. 43, no. 4, pp. 377–384, 1998, [Online]. Available at: https://www.tandfonline.com/doi/abs/10.1080/03081089808818538?journalCode=glma20.
- [2]M.-T. Chien and H. Nakazato, “The q-numerical range of a reducible matrix via a normal operator,” Linear Algebra and its Applications, vol. 419, no. 2-3, pp. 440–465, 2006, [Online]. Available at: https://www.sciencedirect.com/science/article/pii/S0024379506002606.
- [3]M.-T. Chien and H. Nakazato, “Davis–Wielandt shell and q-numerical range,” Linear Algebra and its Applications, vol. 340, no. 1-3, pp. 15–31, 2002, [Online]. Available at: https://core.ac.uk/download/pdf/82029923.pdf.
- [4]N.-K. Tsing, “The constrained bilinear form and the C-numerical range,” Linear Algebra and its Applications, vol. 56, pp. 195–206, 1984, [Online]. Available at: https://core.ac.uk/download/pdf/81931476.pdf.
- [5]R. Koide and H. Nakazato, “The q-numerical range of a certain 3\times 3 matrix,” International Mathematical Forum3, vol. 0, pp. 1001–1010, 2008, [Online]. Available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.672.1372&rep=rep1&type=pdf.