Perturbation of the numerical range of unitary matrices
Let us consider two unitary matrices - matrix $U \in \mathrm{U}(\mathbb{C}^d)$ and its perturbation $V \in \mathrm{U}(\mathbb{C}^d)$, such that $\|U-V\| \le \epsilon$, for some $\epsilon > 0$. To connect those unitary matrices, we define a geodesic curve $U(t) \in \mathrm{U}(\mathbb{C}^d)$ for any $t \in [0,1]$ with boundary conditions $U(0) \coloneqq U$ and $U(1) \coloneqq V$. This smooth path is explicitly given as [1]
\begin{equation} t \mapsto U \exp \left( t \text{Log} \left( U^\dagger V \right) \right). \end{equation}
We will study how the numerical range $W(U(t))$ changes depending on $t$. As shown in [2] we may focus on equivalent, but simplified problem of determining the behavior of the numerical range of $U(t) = U \exp \left( \ii t D_+ \right)$, where $D_+ = \sum_{i = 1}^d p_i \proj{i}$ is diagonal, positive, semi-definite matrix, such that $\sum_{i = 1}^d p_i = 1$.
For a given matrix $M$, let us define a multiset of eigenvalues of the matrix $M$ denoted by $\lambda(M)$. Let $r(\lambda)$ be an algebraic multiplicity of eigenvalue $\lambda \in \lambda(M)$, define by $I_{M, \lambda}$ the isometry which columns are formed by eigenvectors corresponding to eigenvalue $\lambda$ and define
\begin{equation} S_{\lambda}^{M} = \left\{ \ket{x} \in \mathbb{C}^d: (\lambda \1_d - M) \ket{x} = 0, \,\, \| x \|_2 = 1 \right\}. \end{equation}
Theorem [2]
Let $U \in \mathrm{U}(\mathbb{C}^d)$ be a unitary matrix with spectral decomposition
\begin{aligned} U = \sum_{j=1}^d \lambda_j \proj{\lambda_j}. \end{aligned}
Assume that the eigenvalue $\lambda \in \lambda(U)$ is such that $r(\lambda) = k$. Let us define a matrix $V(t)$ given by
\begin{aligned} V(t) = \exp(\ii tD_+) = \sum_{i=1}^d e^{\ii p_it} \proj{i} \in \mathcal{DU}\left(\mathbb{C}^d\right), \quad t \ge 0. \end{aligned}
Let $\lambda(t):=\lambda(UV(t))$ and let every $\lambda_j(t) \in \lambda(t)$ corresponds to eigenvector $\ket{x_j(t)}$. Assume that $\lambda_{1}(t), \ldots, \lambda_{k}(t)$ are such eigenvalues that $\lambda_{j}(t) \to \lambda$, as $t \to 0$. Then:
-
If $ \min\{ \sum_{i=1}^d p_i |\braket{i}{x}|^2: \ket{x} \in S^{U}_{\lambda} \}=0$, then $\lambda$ is an eigenvalue of $UV(t)$.
-
If $| \{ p_i: p_i >0 \} |=l<k$, then $\lambda$ is an eigenvalue of $UV(t)$ and $r(\lambda) \ge k-l$.
-
Each eigenvalue of product $UV(t)$ moves counterclockwise or stays in the initial position as parameter $t$ increases.
-
If $k=1$, then \begin{equation} \lambda_1(t) \simeq \lambda \exp \left( \ii t \sum_{i=1}^d p_i | \braket{i}{x_1} |^2 \right) \end{equation} for small $t \ge 0$.
-
Let $Q \coloneqq I_{U,\lambda}^\dagger D_+ I_{U,\lambda}$ and $\lambda_1(Q) \le \lambda_2(Q) \le \ldots \le \lambda_k(Q)$. Then we have \begin{equation} \lambda_j(t) \simeq \lambda \exp(\ii \lambda_j(Q)t) \end{equation} for small $t \ge 0$ and eigenvector $\ket{x_j}$ corresponding to $\lambda_j \in \lambda(U)$ is given by \begin{equation} \ket{x_j} = I_{U, \lambda} \ket{v_j}, \end{equation} where $\ket{v_j} \in S^{Q}_{\lambda_j(Q)}$.
-
For each $j=1,\ldots,d$ we have
\begin{equation} \frac{\partial}{\partial t} \lambda_j(t) = \ii \lambda_j(t) \sum_{i = 1}^d p_i | \braket{i}{x_j(t)} | ^2. \end{equation}
Moreover,
\begin{equation} \sum_{j=1}^{d} \left| \frac{\partial}{\partial t} \lambda_j(t) \right| = 1. \end{equation}
Intuitively speaking, this theorem gives us hints, which one can use to predict a behavior of $W(UV(t))$. Observe that, the postulate $6.$ fully determines the movenment of the spectrum. However, this is a theoretical statement and in practice, determining the function $t \mapsto \ket{x_j(t)}$ is a numerically complex task. The postulates from $1.$ to $5.$ play a key role in numerical calculations of $W(UV(t))$. The most important fact comes from $3.$, which says that all eigenvalues move in the same direction or stay in the initial position. The instantaneous velocity of a given eigenvalue in general case is given in $5.$, while in the case of eigenvalue with multiplicity equal one, the instantaneous velocity is determined by $4.$. We see that whenever the spectrum of the matrix $U$ is not degenerated, calculating these velocities is an easy task. Eventually, it is worth noting that the postulates $4., 5.$ give us only an approximation of the velocities, so despite being useful in numerical calculations, these expressions are valid only in the neighbourhood of $t=0$.
Illustration of the above theorem
For each eigenvalue $\lambda(t)$ of matrix $UV(t)$ we mark its instantaneous velocity given by formula $\sum_{i=1}^d p_i | \braket{i}{x(t)}|^2 $, where $\ket{x(t)}$ is the corresponding eigenvector. Red color denotes instantaneous velocity equal to one and blue color corresponds to the instantaneous velocity equal to zero.
Example 1
Diagonal matrix $U= \begin{pmatrix} 1 & 0 & 0 & 0 \newline 0 & \ii & 0 & 0 \newline 0 & 0 & -1 & 0 \newline 0 & 0 & 0 & -\ii \newline \end{pmatrix}. $
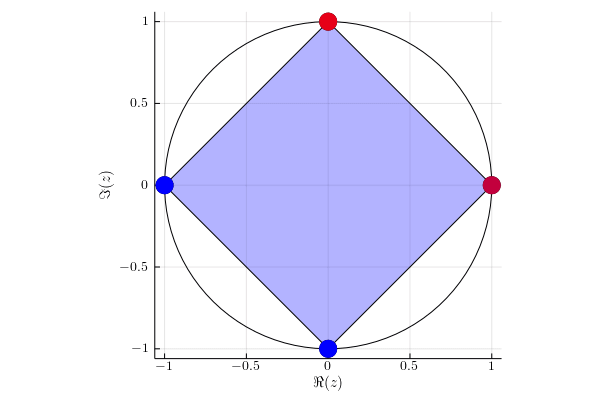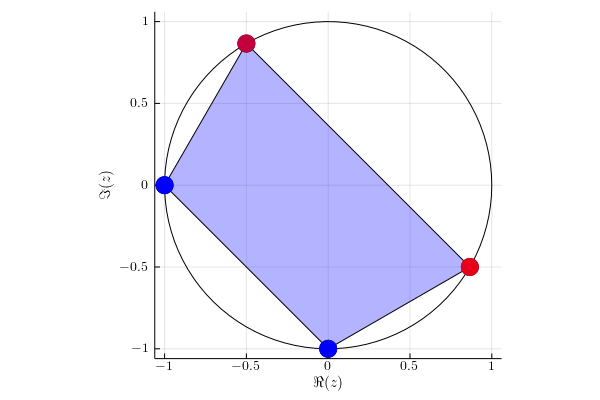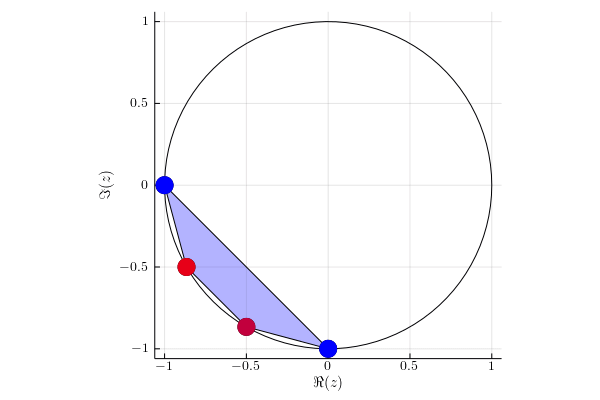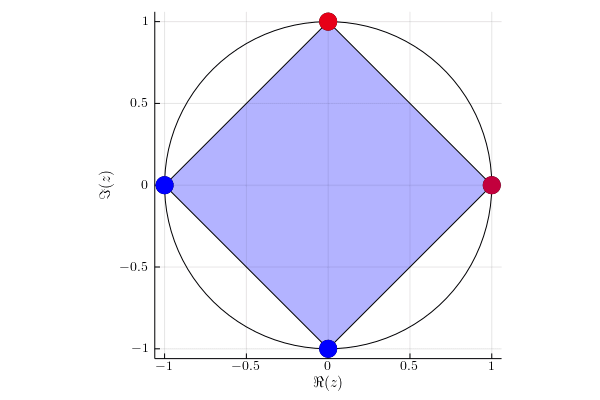
We act on two subspaces with probability $p_1 = 1/3$ and $p_2 = 2/3$. Eigenvalues $-1$ and $-\ii$ stay in the initial position, because they lie on the orthogonal subspace to subspace of which we are acting on.
Example 2
Random matrix $U$ of dimension $3 \times 3$. 
Probability vector is equal to $p = (1,0,0)$. All eigenvalues have nonzero velocity, so degeneration is impossible.
Example 3
Matrix $U$ of dimension $5\times 5$ having eigenbasis given by the Fourier matrix. 
Probability vector is equal to $p = (3/8,1/4,1/4,1/8,0)$. As standard basis and Fourier basis are mutually unbiased, the velocities are similar, which implies the shape of numerical range slightly changes in time.
Example 4
Matrix $U$ with eigenvalues $(1,e^{\ii \pi /6}, \ii , \ii , \ii , -1, -1)$. 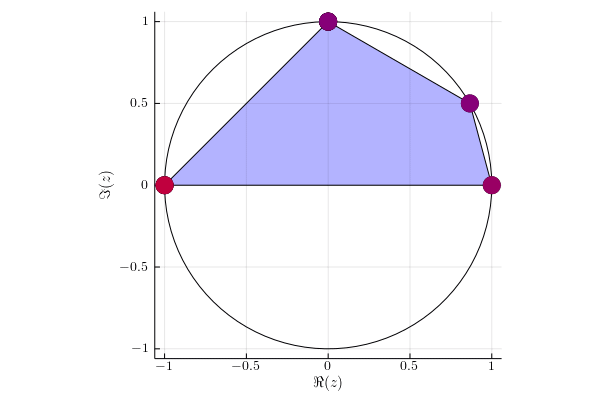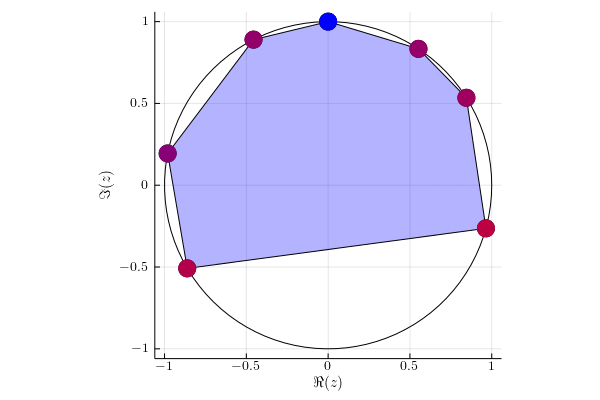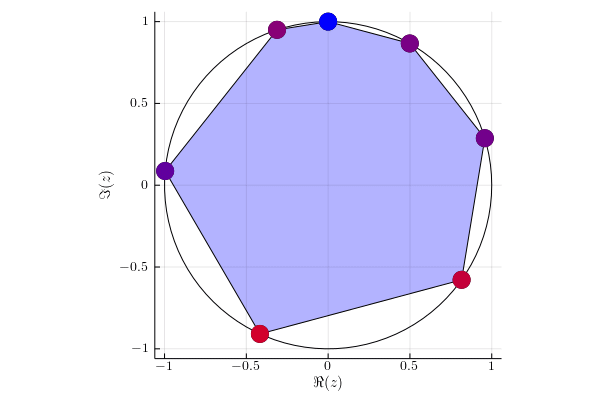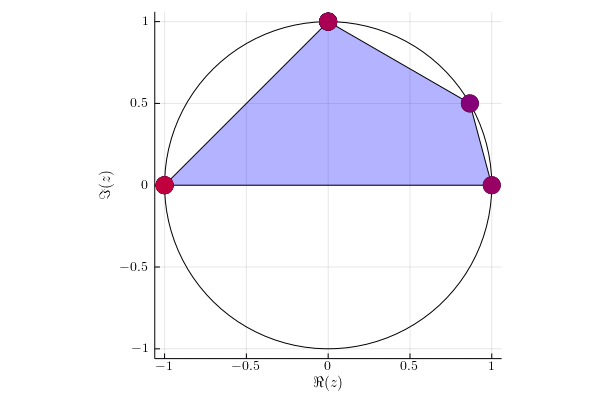
We act on two subspaces with probability $p_1 = 1/3$ and $p_2 = 2/3$. In this case the eigenvalue $\ii$ is three fold degenerated, so it stays in the initial position.
More examples can be found in [2].
References
- [1]J. Antezana, G. Larotonda, and A. Varela, “Optimal paths for symmetric actions in the unitary group,” Communications in Mathematical Physics, vol. 328, no. 2, pp. 481–497, 2014, [Online]. Available at: https://link.springer.com/article/10.1007/s00220-014-2041-x.
- [2]K. Ryszard, L. Paulina, and P. Łukasz, “Perturbation of the numerical range of unitary matrices,” arXiv preprint arXiv: 2002.05553v1, vol. 0, 2020, [Online]. Available at: https://arxiv.org/abs/2002.05553.