$k$-numerical range

Definition

Let $A$ be an $d \times d$ matrix and $P_k$ be a projector of rank $k$. The $k$-numerical range of $A$ is the set \[ W_k(A) = \{ z : z=P_k A \} \]

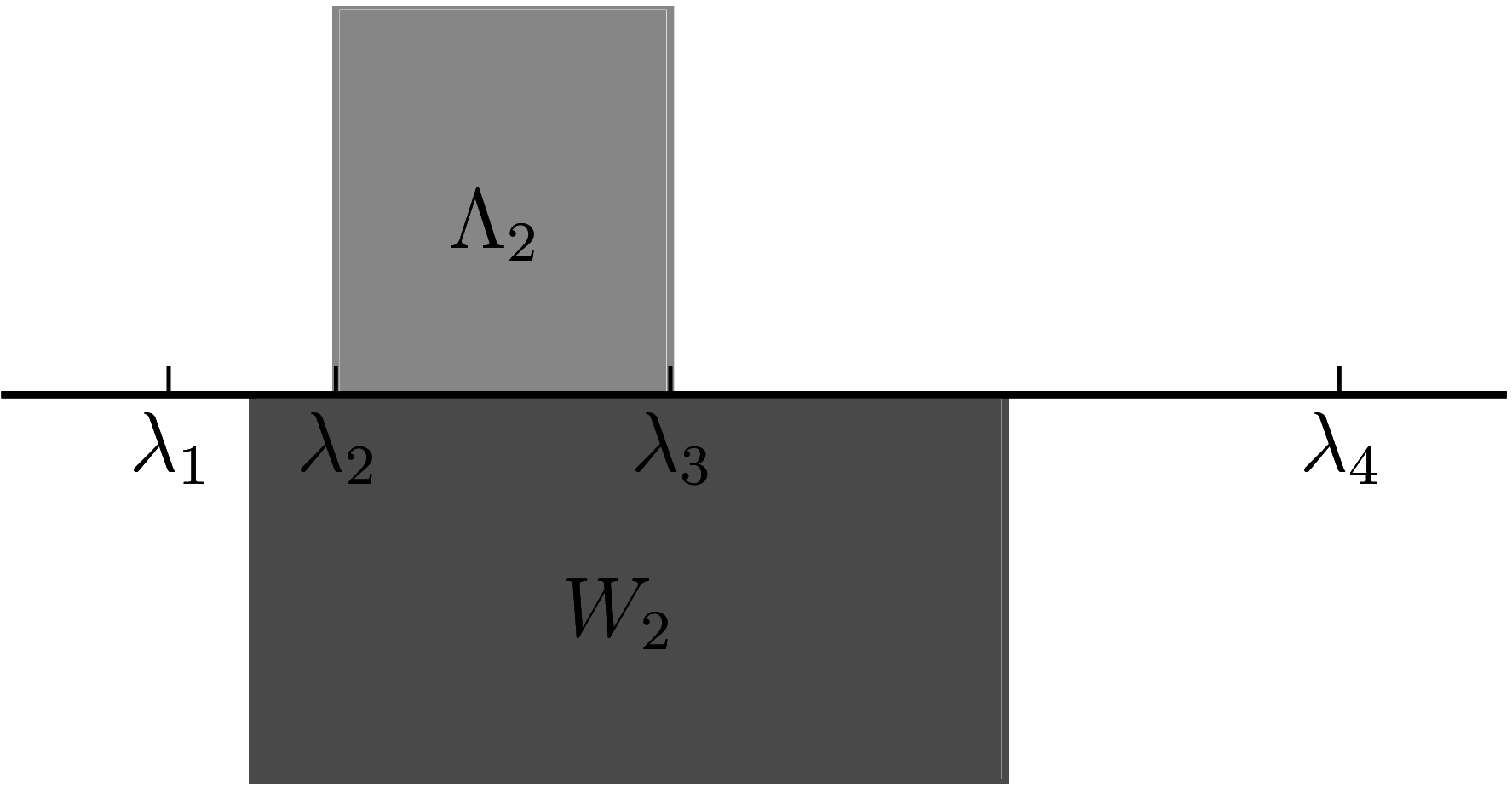
Note that, this numerical range is different from the higher-rank-numerical-range as for a Hermitian matrix $A$, we get \[ W_k = [{i=1}^{k*i, *{i=0}}{k-1} *{d-i} ]. \] where $\lambda_i$ are the eigenvalues of $A$ in an increasing order. On the other hand, the higher-rank-numerical-range is given by \[ _k(A) = [k, *{d-k+1}], \] Hence, we get \[ _k(A) W_k(A). \] We should note that in the case when $k=1$ the $k$-numerical range becomes the standard numerical range \[ W_1(A) = W(A) = _1(A). \]

Examples

A comparison between the k-numerical range and higher-rank numerical range in the case $k=2$. Note that $\Lambda_2 \subset W_2$. The matrix used in this example is $A = \mathrm{diag}(1, 2, 4, 8)$.