Examples

Example 1

Diagonal matrix $A=\begin{pmatrix} 1 & 0 & 0 & 0\ 0 & 1+2\ii & 0 & 0\ 0 & 0 & 3\ii & 0\ 0 & 0 & 0 & 0 \end{pmatrix}$ with respect to matrix $B =\1_4$.

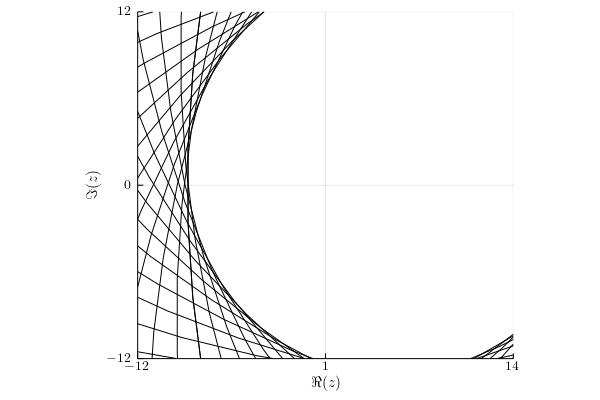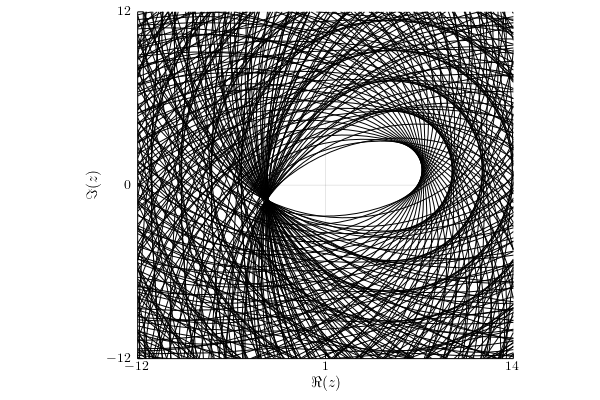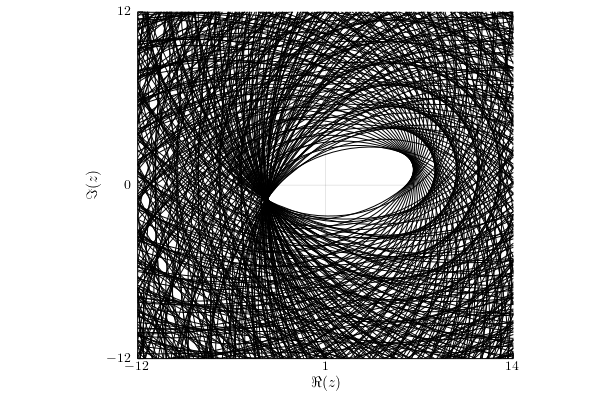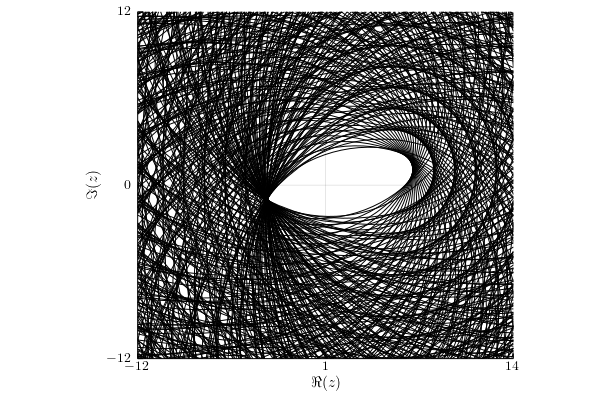
Trace norm

Hilbert-Schmidt norm

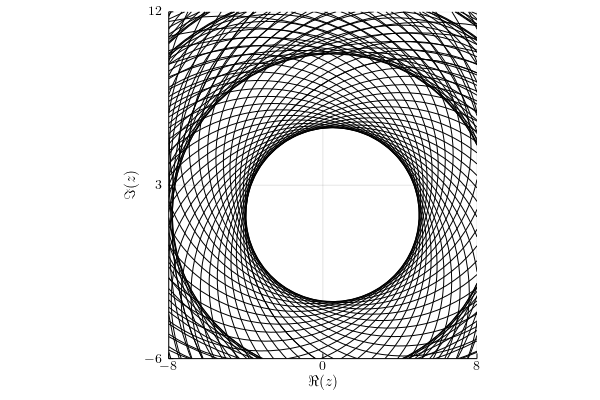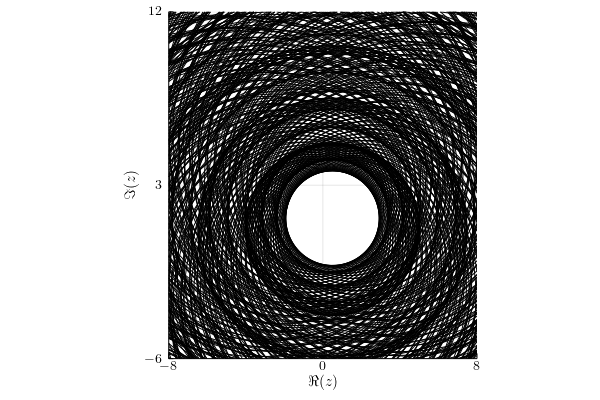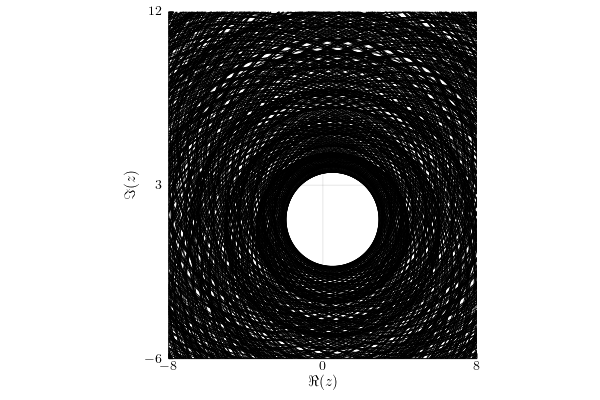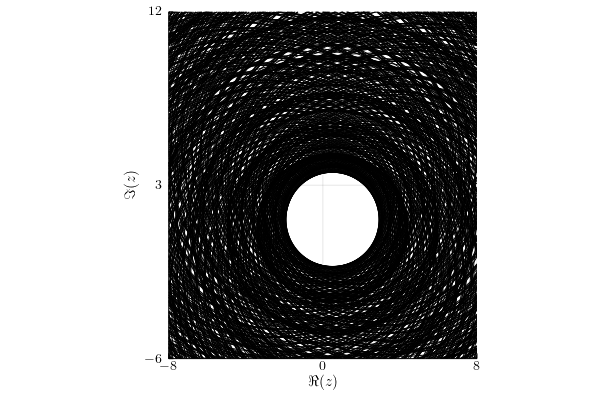
Infinity norm

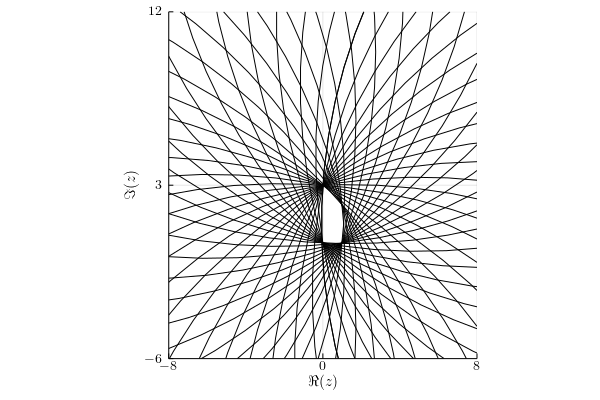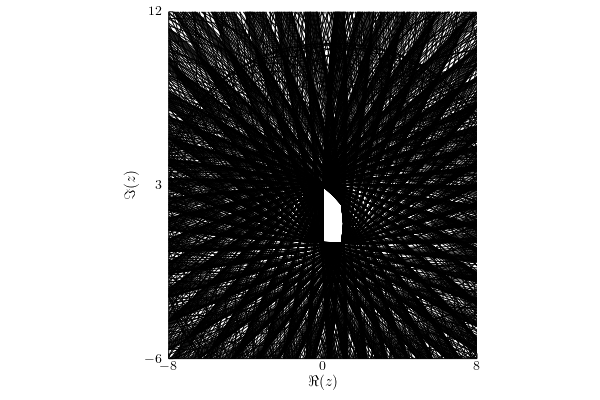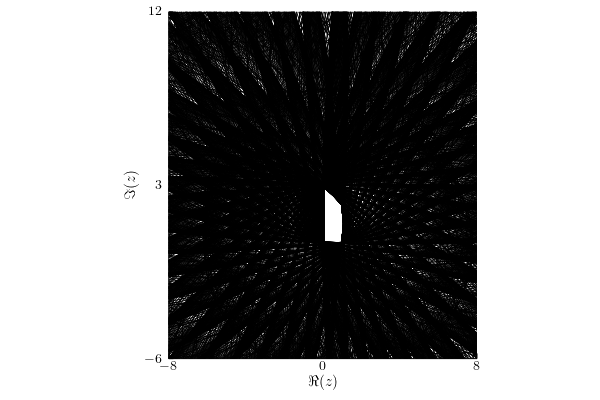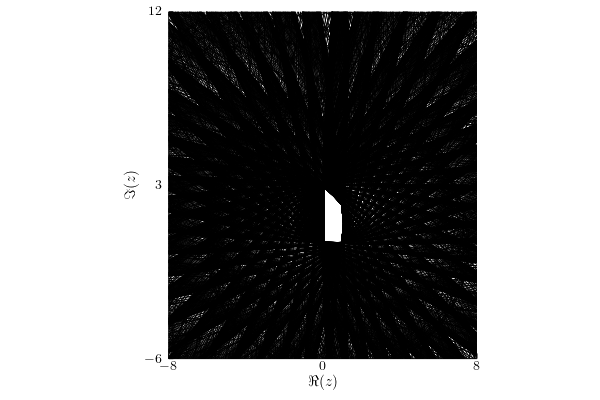Under this assumption, the numerical range $w_{||\cdot||_\infty}(A;\1_4)= W(A)$.

Example 2

Matrix $A=\begin{pmatrix} 6+\ii & 0.4 & 0 & -0.1\ 0.1 & 1-3\ii & -0.3\ii & 0\ 0 & 0 & 0.5 & 0 \end{pmatrix}$ with respect to matrix $B=\begin{pmatrix} 1.2 & 0 & 0 & 0\ 0 & \ii & 0 & 0\ 0 & 0 & -1 & 0 \end{pmatrix}$

Trace norm

Hilbert-Schmidt norm

Infinity norm